Population ecologists make use of a variety of methods to model population dynamics. An accurate model should be able to describe the changes occurring in a population and predict future changes.
Population Growth
The two simplest models of population growth use deterministic equations (equations that do not account for random events) to describe the rate of change in the size of a population over time. The first of these models, exponential growth, describe populations that increase in numbers without any limits to their growth. The second model, logistic growth, introduces limits to reproductive growth that become more intense as the population size increases. Neither model adequately describes natural populations, but they provide points of comparison.
Exponential Growth
In developing his theory of natural selection, Charles Darwin was influenced by the English clergyman Thomas Malthus. Malthus published his book in 1798, stating that populations with abundant natural resources grow very rapidly. However, they limit further growth by depleting their resources. The early pattern of accelerating population size is called exponential growth (Figure 1).
The best example of exponential growth in organisms is seen in bacteria. Bacteria are prokaryotes that reproduce quickly, about an hour for many species. If 1000 bacteria are placed in a large flask with an abundant supply of nutrients (so the nutrients will not become quickly depleted), the number of bacteria will have doubled from 1000 to 2000 after just an hour. Each of the 2000 bacteria will divide in another hour, producing 4000 bacteria. After the third hour, there should be 8000 bacteria in the flask. The important concept of exponential growth is that the growth rate—the number of organisms added in each reproductive generation—is itself increasing; that is, the population size is increasing at a greater and greater rate. After 24 cycles, the population would have increased from 1000 to more than 16 billion bacteria. A J-shaped growth curve is produced when the population size, N, is plotted over time (Figure 1).
The bacteria-in-a-flask example does not truly represent the real world, where resources are usually limited. However, when a species is introduced into a new habitat that it finds suitable, it may show exponential growth for a while. In the case of the bacteria in the flask, some bacteria will die during the experiment and thus not reproduce; therefore, the growth rate is lowered from a maximal rate in which there is no mortality.
Logistic Growth
Extended exponential growth is possible only when infinite natural resources are available; this is not true in the real world. Charles Darwin recognized this fact in his description of the “struggle for existence,” which states that individuals will compete, with members of their own or other species, for limited resources. The successful ones are more likely to survive and pass on the traits that made them successful to the next generation at a greater rate (natural selection). Population ecologists developed the logistic growth model to model the reality of limited resources.
Carrying Capacity and the Logistic Model
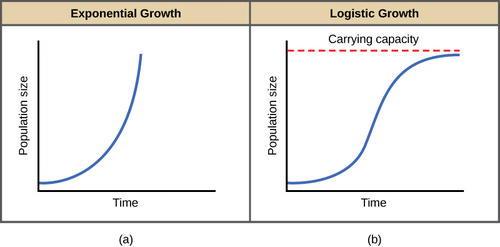
With limited resources, exponential growth cannot continue indefinitely in the real world. Exponential growth may occur in environments with few individuals and plentiful resources. However, when the number of individuals gets large enough, resources will be depleted, and the growth rate will slow down. Eventually, the growth rate will plateau or level off (Figure 1). This population size, which is determined by the maximum population size that a particular environment can sustain, is called the carrying capacity, symbolized as K. In real populations, a growing population often overshoots its carrying capacity, and the death rate increases beyond the birth rate, causing the population size to decline back to the carrying capacity or below it. Most populations usually fluctuate around the carrying capacity in an undulating fashion rather than existing right at it. A graph of logistic growth yields the S-shaped curve (Figure 1). It is a more realistic model of population growth than exponential growth. There are three different sections to an S-shaped curve. Initially, growth is exponential because few individuals and ample resources are available. Then, as resources begin to become limited, the growth rate decreases. Finally, the growth rate levels off at the environment’s carrying capacity, with little change in population number over time.
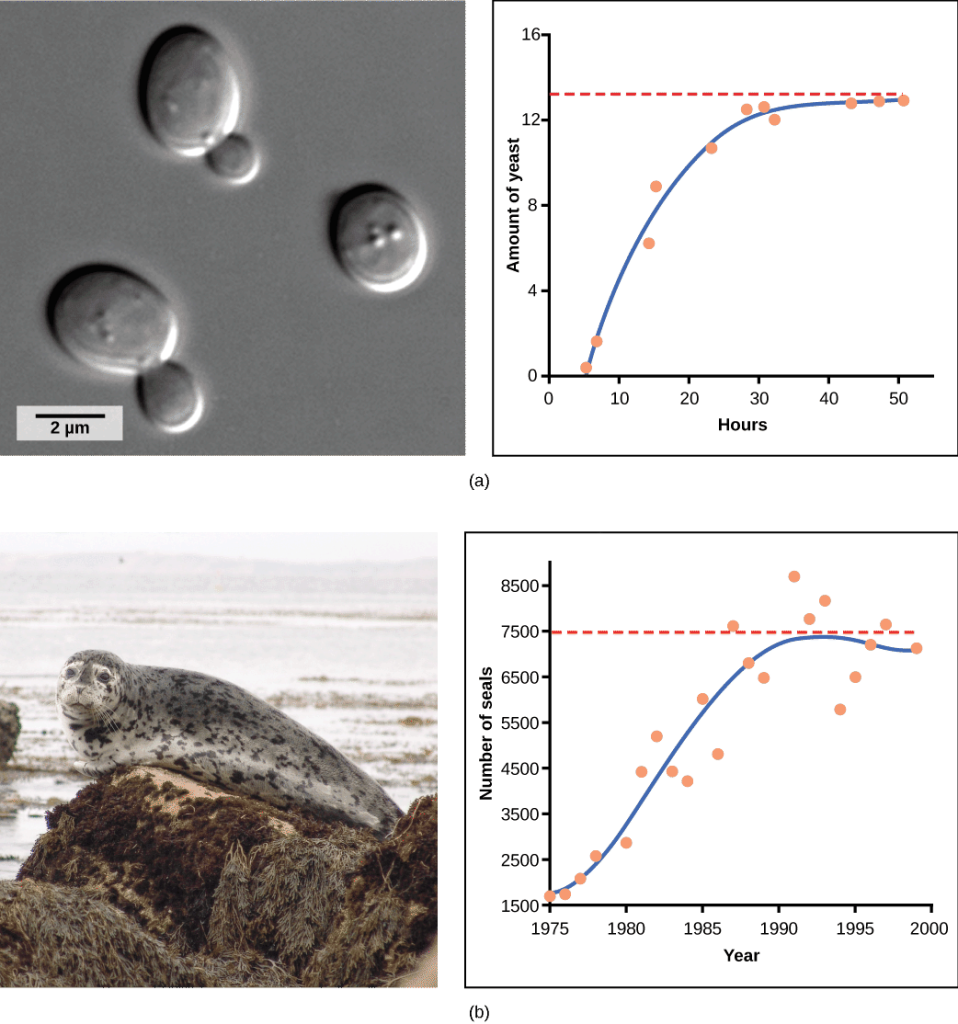
Examples of Logistic Growth
Yeast, a unicellular fungus used to make bread and alcoholic beverages, exhibits the classical S-shaped curve when grown in a test tube (Figure 2a). Its growth levels off as the population depletes the nutrients necessary. In the real world, however, there are variations to this idealized curve. Examples of wild populations include sheep and harbor seals (Figure 2b). In both examples, the population size exceeds the carrying capacity for short periods of time and then falls below the carrying capacity afterward. This fluctuation in population size continues to occur as the population oscillates around its carrying capacity. Still, even with this oscillation, the logistic model is confirmed.
Population Dynamics and Regulation
Why Did the Woolly Mammoth Go Extinct?

Most populations of woolly mammoths went extinct about 10,000 years ago, soon after paleontologists believe humans began to colonize North America and northern Eurasia (Figure 3). A mammoth population survived on Wrangel Island in the East Siberian Sea and was isolated from human contact until as recently as 1700 BC. We know a lot about these animals from carcasses found frozen in the ice of Siberia and other northern regions. It is commonly thought that climate change and human hunting led to their extinction. A 2008 study estimated climate change reduced the mammoth’s range from 3,000,000 square miles 42,000 years ago to 310,000 square miles 6,000 years ago.2

