2 Graphical Descriptions of Data

 

In chapter 1, you were introduced to the concepts of population, which again is a collection of all the measurements from the individuals of interest. Remember, in most cases you can’t collect the entire population, so you have to take a sample. Thus, you collect data either through a sample or a census. Now you have a large number of data values. What can you do with them? No one likes to look at just a set of numbers. One thing is to organize the data into a table or graph. Ultimately though, you want to be able to use that graph to interpret the data, to describe the distribution of the data set, and to explore different characteristics of the data. The characteristics that will be discussed in this chapter and the next chapter are:

• Center: middle of the data set, also known as the average.
• Variation: how much the data varies.
• Distribution: shape of the data (symmetric, uniform, or skewed).
• Qualitative data: analysis of the data
• Outliers: data values that are far from the majority of the data.
• Time: changing characteristics of the data over time.

This chapter will focus mostly on using the graphs to understand aspects of the data, and not as much on how to create the graphs. There is technology that will create most of the graphs, though it is important for you to understand the basics of how to create them.

This textbook uses R Studio to perform all graphical and descriptive statistics, and all statistical inference. When using R Studio, every command is performed the same way. You start off with a goal(explanatory variable ~ response variable, data=data frame_name,…)

R Studio uses packages to make calculations easier. For this textbook, you will 37

 

 

mostly need the package mosaic. There will be others that you will need on occasion, but you will be told that at the time. Most likely, mosaic is already installed in your R Studio. If you wish to install other packages you use the command

install.packages(“name of package”)

where you replace the name of package with the package you wish to install.

Once the package is installed, then you will need to tell R Studio you want to use it every time you start R Studio. The command to tell R Studio you want to use a package is

library(“name of package”)

You will need to turn on the package mosaic. The NHANES package contains a data frame that is useful. Both are accessed by doing.

library(“mosaic”) library(“NHANES”) library(“StatsUsingTechnologyData”)

Back to the basic command

goal(explanatory variable ~ response variable, data=data frame_name,…)

The goal depends on what you want to do. If you want to create a graph then you would need

gf_graphtype(explanatory variable ~response variable, data=dataframe_name, …)

As an example if you want to create a density plot of cholesterol levels on day 2 from a dataframe called Cholesterol, then your command would be

gf_density(~day2, data=Cholesterol)

You will see more on what the different commands are that you would use. A word about the … at the end of the command. That means there are other things you can do, but that is up to you if you want to actually do them. They do not need to be used if you don’t want to. The following sections will show you how to create the different graphs that are usually completed in an introductory statistics course.

 

 

 

 

Qualitative Data

Remember, qualitative data are words describing a characteristic of the individ- ual. There are several different graphs that are used for qualitative data. These

 

 

graphs include bar graphs, Pareto charts, and pie charts. Bar graphs can be created using a statistical program like R Studio.

Bar graphs or charts consist of the frequencies on one axis and the cate- gories on the other axis. Drawing the bar graph using R is performed using the following command.

gf_bar(~explanatory variable, data=Dataframe)

 

Example: Drawing a Bar Chart**

Data was collected for two semesters in a statistics class. The data frame in is the table #2.1.1. The command

head(data frame)

shows the variables and the first few lines of the data set.

Table #2.1.1: Statistics class survey

Class<-read.csv( “https://krkozak.github.io/MAT160/class_survey.csv”)head(Class)

##vehicle gender distance_campusice_cream rent

##	1	None	Female	1.5	Cookie Dough	724
##	2	Mercury	Female	14.7	Sherbet	200
##	3	Ford	Female	2.4	Chocolate Brownie.	600
##	4	Toyota	Female	5.2	coffee	0
##	5	Jeep	Male	2.0	Cookie Dough	600
##	6	Subaru	Male	5.0	none	500
##					major height

## 1 Environmental and Sustainability Studies61

## 2Administrative Justice60

## 3Bio Chem68

## 466

## 5Pre-health Careers71

## 6Finance72

##winter

## 1 Liked it ## 2 Don’t like it ## 3 Liked it

## 4 Loved it

## 5 Loved it

## 6 No opinion

Every data frame has a code book that describes the data set, the source of the data set, and a listing and description of the variables in the data frame.

Code book for Data Frame Class

 

 

Description Survey results from two semesters of statistics classes at Coconino Community College in the years 2018-2019.

Format

This data frame contains the following columns:

vehicle: Type of car a student drives gender: Self declared gender of a student

distance_campus: how far a student lives from the Lone Tree Campus of Co- conino Community College (miles)

ice_cream: favorite ice cream flavor rent: How much a student pays in rent major: Students declared major height: height of the student (inches)

winter: Student’s opinion of winter (Love it, Like it, Don’t like, No opinion)

Source

Kozak K (2019). Survey results form surveys collected in statistics class at Coconino Community College.

References

Kozak, 2019

Create a bar graph of vehicle type. To do this in R Studio, use the command

gf_bar(~variable, data=DataFrame, …)

 

where gf_bar is the goal, vehicle is the name of the response variable (there is no explanatory variable), the dataframe is Class, and a title was added to the graph.

gf_bar(~vehicle, data=Class, title=”Cars driving by students in statistics class”)

Notice from the graph (Figure 2.1), you can see that Chevrolet and Ford are the more popular car, with Jeep, Subaru, and Toyota not far behind. Many types seems to be the lesser used, and tied for last place. However, more data would help to figure this out.

• All graphs should have labels on each axis and a title for the graph.*

The beauty of data frames with multiple variables is that you can answer many questions from the data. Suppose you want to see if gender makes a difference for the type of car a person drives. If you are a car manufacturer, if you knew that certain genders like certain cars, then you would advertise to the different

 

 

Cars driving by students in statistics class

 

4

 

 

 

 

3

 

 

 

 

count
2

 

 

 

 

1

 

 

 

 

0

Audi Buick ChevroletDodge Ford Honda Hyundai Jeep Mercury Nissan None Subaru Toyota

vehicle

 

Figure 2.1: Bar Graph for Type of Car Data

 

 

gf_bar(~vehicle|gender, data=Class, title=”Cars driving by students in statistics class”)
genders. To create a bar graph that separates based on gender, perform the following command in R Studio.

Notice a Ford is driven by females more than any other car, while Chevrolet, Mercury, and Subaru cars are equally driven by males. Obviously a larger sample would be needed to make any conclusions from this data.

There are other types of graphs that can be created for quantitative variables. Another type is known as a dot plot. The command for this graph (Figure 2.3) is as follows.

gf_dotplot(~vehicle, data=Class, title=”Cars driving by students in statistics class”)

 

## `stat_bindot()` using `bins = 30`. Pick better value with `binwidth`.

Notice a dot plot is like a bar chart. Both give you the same information. You can also divide a dot plot by gender. Another type of graph that is also useful and similar to the dot plot is a point plot (scatter plot). In this plot (Figure 2.4) you can graph the explanatory variable versus the response variable. The command for this in R Studio is as follows.

 

 

Cars driving by students in statistics class

 

 

Female
Male
4

 

 

 

 

3

 

 

 

 

count
2

 

 

 

 

1

 

 

 

 

0

AudBi uCichkevrDoloedtgFeorHdonHdyaundJaeieMpercNurisysaNnonSeubaTrouyota AudBi uCichkevrDoloedtgFeorHdonHdyaundJaeieMpercNurisysaNnonSeubaTrouyota

vehicle

 

Figure 2.2: Bar Graph for Type of Car Data

 

 

 

 

 

 

1.00

 

 

 

 

0.75

 

 

 

 

count
0.50

 

 

 

 

0.25

 

 

 

 

0.00

Cars driving by students in statistics class

 

Audi Buick ChevroletDodge Ford Honda Hyundai Jeep Mercury Nissan None Subaru Toyota

vehicle

 

Figure 2.3: Dot Plot for Type of Car Data

 

 

gf_point(vehicle~gender, data=Class,title=”Cars driving by students in statistics class”)

 

Cars driving by students in statistics class

 

Toyota

Subaru

None

Nissan

Mercury

vehicle
Jeep

Hyundai

Honda

Ford

Dodge

Chevrolet

Buick

Audi

FemaleMale

gender

 

Figure 2.4: Point plot for Type of Car Data versus gender

 

gf_jitter(vehicle~gender, data=Class, title=”Cars driving by students in statistics class”)
The problem with this graph (Figure 2.4) is that if there are multiple females who drive a Ford, only one dot is shown. So it is best to spread the dots out using a plot known as a jitter plot. In a jitter plot the dots are randomly moved off the center line. The command for a jitter plot is as follows:

 

Now you can see (Figure 2.5) that there are 4 females who drive a Ford. There is one female who drives a Honda. Other information about other cars and genders can be seen better than in the point plot and the bar graph. Jitter plots are useful to see how many data values are for each qualitative data values.

 

There are many other types of graphs that can be used on qualitative data. There are spreadsheet software packages that will create most of them, and it is better to look at them to see how to create then. It depends on your data as to which may be useful, but the bar, dot, and jitter plots are really the most useful.

 

 

Cars driving by students in statistics class

 

vehicle
























Toyota Subaru None Nissan Mercury Jeep Hyundai Honda Ford Dodge Chevrolet

Buick Audi

FemaleMale

gender

 

Figure 2.5: Jitter plot for Type of Car Data versus gender

 

Homework

• Eyeglassomatic manufactures eyeglasses for different retailers. The num- ber of lenses for different activities is in table #2.1.2.

Table #2.1.2: Data for Eyeglassomatic

Eyeglasses<-read.csv( “https://krkozak.github.io/MAT160/eyglasses.csv”)head(Eyeglasses)

## activity

## 1	Grind
## 2	Grind
## 3	Grind
## 4	Grind
## 5	Grind
## 6	Grind

Code book for Data Frame Eyeglasses

Description Activities that an Eyeglass company performs when making eye- glasses, Grind means ground the lenses and put them in frames, multicoat means put tinting or coatings on lenses and then put them in frames, assemble means received frames and lenses from other sources and put them together, make

 

 

frames means made the frames and put lenses in from other sources, receive finished means received glasses from other source unknown means do not know where the lenses came from.

Format

This data frame contains the following columns:

activity: The activity that is completed to make the eyeglasses by Eyeglasso- matic

Source John Matic provided the data from a company he worked with. The company’s name is fictitious, but the data is from an actual company.

References John Matic (2013)

Make a bar chart of this data. State any findings you can see from the graph.

• Data was collected for two semesters in a statistics class drive. The data frame in is the table #2.1.3.

Table #2.1.3 Data Frame of Statistics Class Survey

Class<-read.csv( “https://krkozak.github.io/MAT160/class_survey.csv”)head(Class)

##vehicle gender distance_campusice_cream rent

##	1	None Female	1.5Cookie Dough	724
##	2	Mercury Female	14.7Sherbet	200
##	3	Ford Female	2.4 Chocolate Brownie.	600
##	4	Toyota Female	5.2coffee	0
##	5	JeepMale	2.0Cookie Dough	600
##	6	SubaruMale	5.0none	500
##			major height
##	1	Environmental and	Sustainability Studies61
##	2		Administrative Justice60
##	3		Bio Chem68

## 466

## 5Pre-health Careers71

## 6Finance72

##winter

## 1 Liked it ## 2 Don’t like it ## 3 Liked it

## 4 Loved it

## 5 Loved it

## 6 No opinion

Code book for Data Frame Class see Example #2.1.1

 

 

Create a bar graph and dot plot of the variable ice cream. State any findings you can see from the graphs.

• The number of deaths in the US due to carbon monoxide (CO) poisoning from generators from the years 1999 to 2011 are in table #2.1.4 (Hinatov, 2012). Create a bar chart of this data. State any findings you see from the graph.

Table #2.1.4: Data of Number of Deaths Due to CO Poisoning

Area<-read.csv( “https://krkozak.github.io/MAT160/area.csv”)head(Area)

##deaths ## 1 Urban

## 2 Urban

## 3 Urban

## 4 Urban

## 5 Urban

## 6 Urban

• Data was collected for two semesters in a statistics class drive. The data frame in is the table #2.1.5. Create a bar graph and dot plot of the variable major. Create a jitter plot of major and gender. State any findings you can see from the graphs.

**Table #2.1.5 Data Frame of Class Survey

Class<-read.csv( “https://krkozak.github.io/MAT160/class_survey.csv”)head(Class)

##vehicle gender distance_campusice_cream rent

##	1	None	Female	1.5	Cookie Dough	724
##	2	Mercury	Female	14.7	Sherbet	200
##	3	Ford	Female	2.4	Chocolate Brownie.	600
##	4	Toyota	Female	5.2	coffee	0
##	5	Jeep	Male	2.0	Cookie Dough	600
##	6	Subaru	Male	5.0	none	500

##major height

## 1 Environmental and Sustainability Studies61

## 2Administrative Justice60

## 3Bio Chem68

## 466

## 5Pre-health Careers71

## 6Finance72

##winter

## 1Liked it

 

 

## 2 Don’t like it

##	3	Liked it
##	4	Loved it
##	5	Loved it
##	6	No opinion

Code book for Data Frame Class see Example #2.1.1

• Eyeglassomatic manufactures eyeglasses for different retailers. They test to see how many defective lenses they made during the time period of January 1 to March 31. Table #2.1.6 gives the defect and the number of defects. Create a bar chart of the data and then describe what this tells you about what causes the most defects.

Table #2.1.6: Data of Defect Type

Defects<- read.csv( “https://krkozak.github.io/MAT160/defects.csv”)head(Defects)

##type

## 1small

## 2small

## 3pd

## 4 flaked

## 5 scratch

## 6spot

Code book for Data Frame Defects

Description Types of defects that an Eyeglass company sees in the lenses they make into eyeglasses.

Format

This data frame contains the following columns:

type: The type of defect that is Seen when making eyeglasses by Eyeglassomatic

Source John Matic provided the data from a company he worked with. The company’s name is fictitious, but the data is from an actual company.

References John Matic (2013)

• American National Health and Nutrition Examination (NHANES) surveys is collected every year by the US National Center for Health Statistics (NCHS). The data frame is in table #2.1.7. Create a bar chart of Martial- Status. Create a jitter plot of MaritalStatus versus Education. Describe any findings from the graphs.

Table #2.1.7: Data Frame NHANES

 

 

head(NHANES)

 

 

## # A tibble: 6 x 76

##ID SurveyYr GenderAge AgeDecade AgeMonths Race1 ##<int> <fct><fct> <int> <fct><int> <fct>

##	1	51624 2009_10 male	34 ” 30-39″	409	White
##	2	51624 2009_10 male	34 ” 30-39″	409	White
##	3	51624 2009_10 male	34 ” 30-39″	409	White
##	4	51625 2009_10 male	4 ” 0-9″	49	Other
##	5	51630 2009_10 female	49 ” 40-49″	596	White
##	6	51638 2009_10 male	9 ” 0-9″	115	White
##	#	… with 69 more variables: Race3 <fct>, Education <fct>,
##	#	MaritalStatus <fct>, HHIncome <fct>, HHIncomeMid <int>,
##	#	Poverty <dbl>, HomeRooms <int>, HomeOwn <fct>,
##	#	Work <fct>, Weight <dbl>, Length <dbl>, HeadCirc <dbl>,
##	#	Height <dbl>, BMI <dbl>, BMICatUnder20yrs <fct>,
##	#	BMI_WHO <fct>, Pulse <int>, BPSysAve <int>,
##	#	BPDiaAve <int>, BPSys1 <int>, BPDia1 <int>,
##	#	BPSys2 <int>, BPDia2 <int>, BPSys3 <int>, BPDia3 <int>,
##	#	Testosterone <dbl>, DirectChol <dbl>, TotChol <dbl>,
##	#	UrineVol1 <int>, UrineFlow1 <dbl>, UrineVol2 <int>,
##	#	UrineFlow2 <dbl>, Diabetes <fct>, DiabetesAge <int>,
##	#	HealthGen <fct>, DaysPhysHlthBad <int>,
##	#	DaysMentHlthBad <int>, LittleInterest <fct>,
##	#	Depressed <fct>, nPregnancies <int>, nBabies <int>,
##	#	Age1stBaby <int>, SleepHrsNight <int>,
##	#	SleepTrouble <fct>, PhysActive <fct>,
##	#	PhysActiveDays <int>, TVHrsDay <fct>, CompHrsDay <fct>,
##	#	TVHrsDayChild <int>, CompHrsDayChild <int>,
##	#	Alcohol12PlusYr <fct>, AlcoholDay <int>,
##	#	AlcoholYear <int>, SmokeNow <fct>, Smoke100 <fct>,
##	#	Smoke100n <fct>, SmokeAge <int>, Marijuana <fct>,
##	#	AgeFirstMarij <int>, RegularMarij <fct>,
##	#	AgeRegMarij <int>, HardDrugs <fct>, SexEver <fct>,
##	#	SexAge <int>, SexNumPartnLife <int>,
##	#	SexNumPartYear <int>, SameSex <fct>,
##	#	SexOrientation <fct>, PregnantNow <fct>

 

To view the code book for NHANES, type help(“NHANES”) in R Studio after you load the NHANES packages using library(“NHANES”)

 

Quantitative Data

There are several different graphs for quantitative data. With quantitative data, you can talk about how the data is distributed, called a distribution. The shape of the distribution can be described from the graphs.

Histogram: a graph of frequencies (counts) on the vertical axis and classes on the horizontal axis. The height of the rectangles is the frequency and the width is the class width. The width depends on how many classes (bins) are in the histogram. The shape of a histogram is dependent on the number of bins. In R Studio the command to create a histogram is

gf_histogram(~response variable, data=Data Frame, title=”title of the graph”)

The last part of the command puts a title on the graph. You type in what ever you want for the title in the quotes.

Density Plot: Similar to a histogram, except smoothing is created to smooth out the graph. The shape is not dependent on the number of bins so the distri- bution is easier to determine from the density plot. In R Studio the command to create a density plot is

gf_density(~response variable, data=Data Frame, title=”title of the graph”)

The last part of the command puts a title on the graph. You type in what every you want for the title in the quotes.

Dot Plot: Dot plots can be created for both quantitative and qualitative vari- ables. For smaller data frames, a dot plot can be useful to determine the shape of the distribution. The command in R Studio is

gf_dotplot(~response variable, data=Data Frame, title=”title of the graph”)

The last part of the command puts a title on the graph. You type in what ever you want for the title in the quotes.

 

Example: Drawing a Histogram and Density plot

Data was collected for two semesters in a statistics class drive.

Table #2.2.1: Statistis class survey

 

Class<-read.csv( “https://krkozak.github.io/MAT160/class_survey.csv“) head(Class)
##	vehicle gender distance_campus		ice_cream rent
## 1	None Female	1.5	Cookie Dough	724
## 2 Mercury Female		14.7	Sherbet	200

 

 

##	3	Ford	Female	2.4	Chocolate Brownie.	600
##	4	Toyota	Female	5.2	coffee	0
##	5	Jeep	Male	2.0	Cookie Dough	600
##	6	Subaru	Male	5.0	none	500

##major height

## 1 Environmental and Sustainability Studies61

## 2Administrative Justice60

## 3Bio Chem68

## 466

## 5Pre-health Careers71

## 6Finance72

##winter

## 1 Liked it ## 2 Don’t like it ## 3 Liked it

## 4 Loved it

## 5 Loved it

## 6 No opinion

Code book for Data Frame Class See Example #2.1.1.

Draw a histogram, density plot, and a dot plot for the variable the distance a student lives from the Lone Tree Campus of Coconino Community College. Describe the story the graphs tell.

Solution:

gf_histogram(~distance_campus, data=Class, title=”Distance in miles from the Lone Tree Campus”)
gf_density(~distance_campus, data=Class, title=”Distance in miles from the Lone Tree Campus”)
gf_dotplot(~distance_campus, data=Class, title=”Distance in miles from the Lone Tree Campus”)

 

 

## `stat_bindot()` using `bins = 30`. Pick better value with `binwidth`.

Notice the histogram, density plot, and dot plot are all very similar, but the density plot is smother. They all tell you similar ideas of the shape of the distribution. Reviewing the graphs you can see that most of the students live within 10 miles of the Lone Tree Campus, in fact most live within 5 miles from the campus. However, there is a student who lives around 50 miles from the Lone Tree Campus. This is a great deal farther from the rest of the data. This value could be considered an outlier. An outlier is a data value that is far from the rest of the values. It may be an unusual value or a mistake. It is a data value that should be investigated. In this case, the student lived really far from campus, thus the value is not a mistake, and is just very unusual. The density plot is probably the best plot for most data frames.

 

 

Distance in miles

from the Lone Tree Campus

 

 

 

 

 

9

 

 

 

 

count
6

 

 

 

 

3

 

 

 

 

0

01020304050

distance_campus

 

Figure 2.6: Histogram of Distance a Student Lives from the Lone Tree Campus

 

Distance in miles

from the Lone Tree Campus

0.125

 

 

 

0.100

 

 

 

0.075

 

 

 

density
0.050

 

 

 

0.025

 

 

 

0.000

01020304050

distance_campus

 

Figure 2.7: Density plot of Distance a Student Lives from the Lone Tree Campus

 

 

 

 

 

 

 

1.00

 

 

 

 

0.75

 

 

 

 

count
0.50

 

 

 

 

0.25

 

 

 

 

0.00

Distance in miles

from the Lone Tree Campus

 

01020304050

distance_campus

 

Figure 2.8: Dot Plot of Distance a Student Lives from the Lone Tree Campus

 

There are other aspects that can be discussed, but first some other concepts need to be introduced.

** Shapes of the distribution:**

When you look at a distribution, look at the basic shape. There are some basic shapes that are seen in histograms. Realize though that some distributions have no shape. The common shapes are symmetric, skewed, and uniform. Another interest is how many peaks a graph may have. This is known as modal.

Symmetric means that you can fold the graph in half down the middle and the two sides will line up. You can think of the two sides as being mirror images of each other. Skewed means one “tail” of the graph is longer than the other. The graph is skewed in the direction of the longer tail (backwards from what you would expect). A uniform graph has all the bars the same height.

Modal refers to the number of peaks. Unimodal has one peak and bimodal has two peaks. Usually if a graph has more than two peaks, the modal information is not longer of interest.

Other important features to consider are gaps between bars, a repetitive pattern, how spread out is the data, and where the center of the graph is.

Examples of graphs:

 

 

This graph is roughly symmetric and unimodal:

Graph #.2.1: Symmetric Distribution

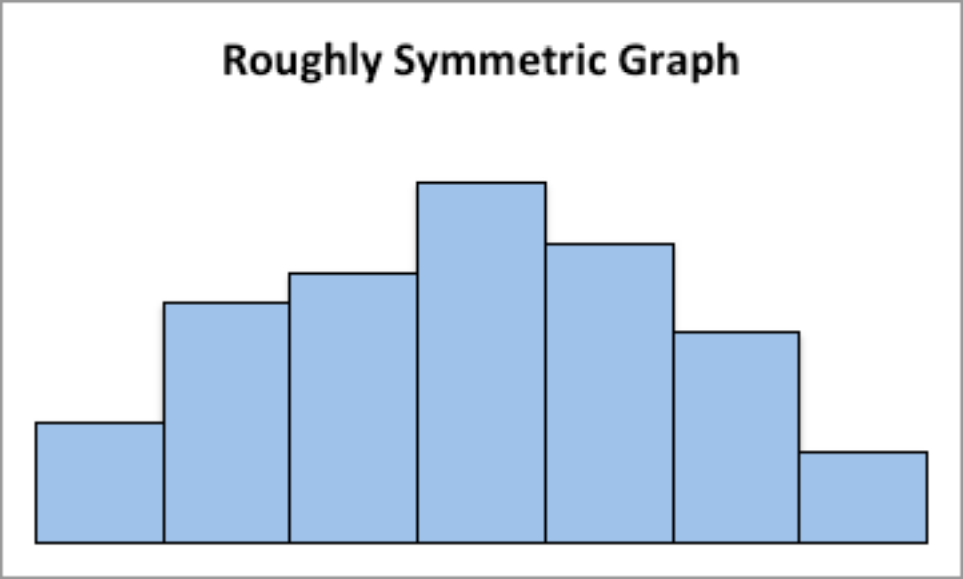
Figure 2.9: Graph of roughly symmetric graph This graph is symmetric and bimodal:

Graph #2.2.2: Symmetric and Bimodal Distribution

This graph is skewed to the right:

Graph #2.2.3: Skewed Right Distribution

This graph is skewed to the left and has a gap:

Graph #2.2.4: Skewed Left Distribution

This graph is uniform since all the bars are the same height:

Graph #2.2.5: Uniform Distribution

 

Example: Drawing a Histogram and Density plot

Data was collected from the Chronicle of Higher Education for tuition from public four year colleges, private four year colleges, and for profit four year colleges. The data frame is in table #2.2.2. Draw a density plot of instate tuition levels for all four year institutions, and then separate the density plot for instate tuition based on type of institution. Describe any findings from the graph.

table #2.2.2: Tuition of Four Year Colleges

Tuition<-read.csv( “https://krkozak.github.io/MAT160/Tuition_4_year.csv”)head(Tuition)

 

 

 

 

 

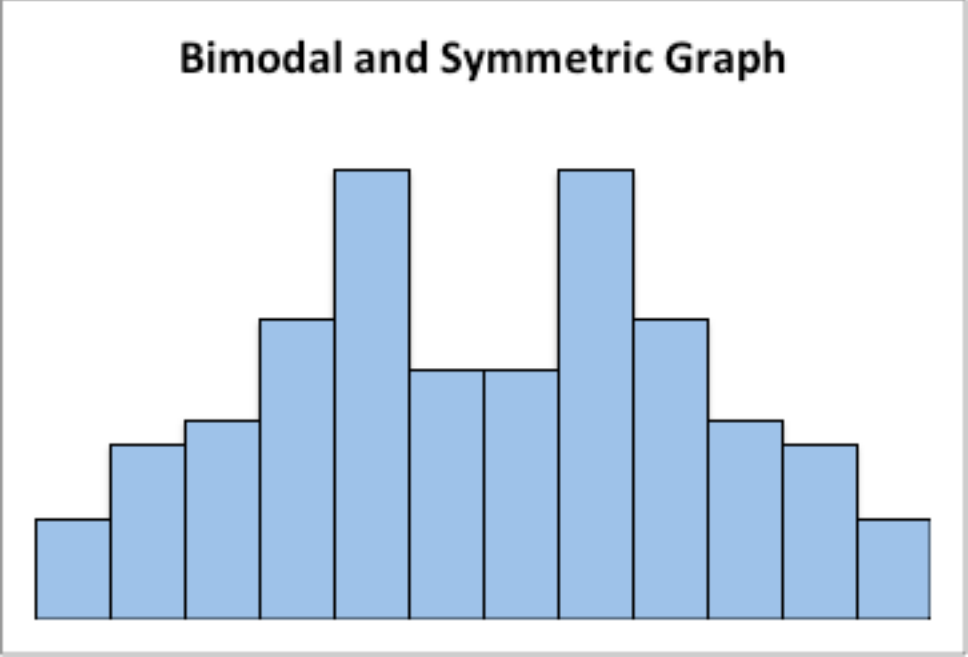
Figure 2.10: Graph of symmetric and bimodal graph

 

 

 

 

 

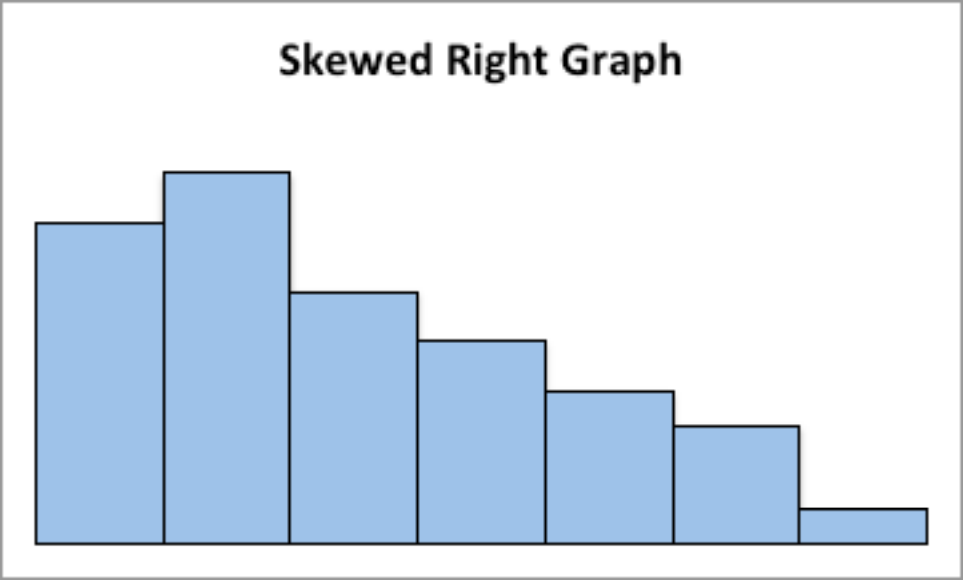
Figure 2.11: Graph of skewed right graph

 

 

 

 

 

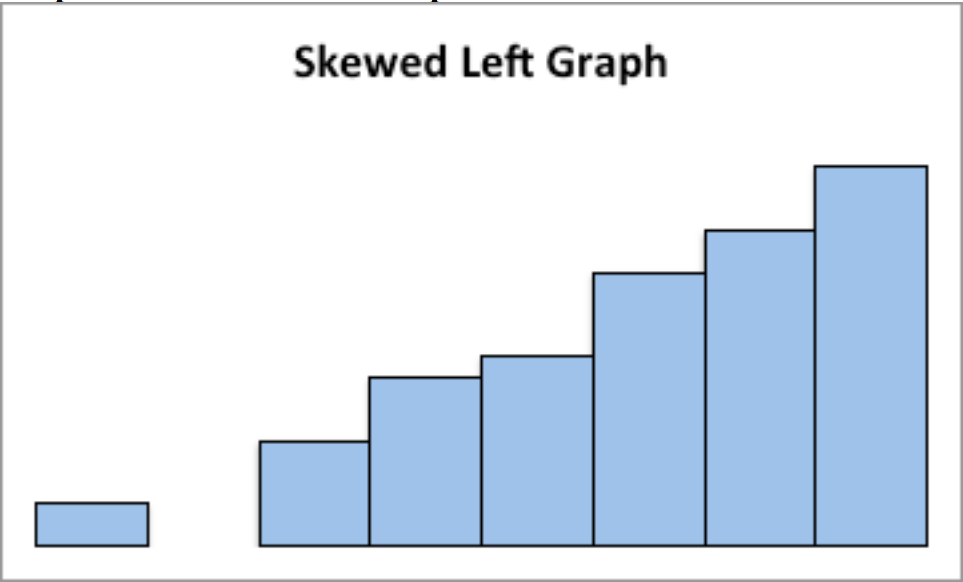
Figure 2.12: Graph of Skewed Left graph

 

 

 

 

 

Figure 2.13: Graph of uniform graph

 

 

##INSTITUTION

## 1University of Alaska AnchoragePublic 4-year

## 2University of Alaska FairbanksPublic 4-year

## 3University of Alaska SoutheastPublic 4-year

## 4Alaska Bible CollegePrivate 4-year

## 5Alaska Pacific UniversityPrivate 4-year ## 6 Alabama Agricultural and Mechanical UniversityPublic 4-year ##TYPE STATE ROOM_BOARD INSTATE_TUITION

## 1		Public_4 year	AK	12200	7688
## 2		Public_4 year	AK	8930	8087
## 3		Public_4 year	AK	9200	7092
## 4 Private_4_year			AK	5700	9300
## 5 Private_4_year			AK	7300	20830
## 6		Public_4 year	AL	8379	9698
##		INSTATE_TOTAL	OUTOFSTATE_TUITION		OUTOFSTATE_TOTAL
##	1	19888	23858		36058
##	2	17017	24257		33187
##	3	16292	19404		28604
##	4	15000	9300		15000
##	5	28130	20830		28130
##	6	18077	17918		26297

Code book for Data Frame Tuition Description Cost of four year institutions. Format

This data frame contains the following columns: INSTITUTION: Name of four year institution

TYPE: Type of four year institution, Public_4_year, Private_4_year, For_profit_4_year.

STATE: What state the institution resides

ROOM_BOARD: The cost of room and board at the institution ($) INSTATE_TUTION: The cost of instate tuition ($)

INSTATE_TOTAL: The cost of room and board and instate tuition ($ per year)

OUTOFSTATE_TUTION: The cost of out of state tuition ($ per year)

OUTOFSTATE_TOTAL: The cost of room and board and out of state tuition ($ per year)

Source Tuition and Fees, 1998-99 Through 2018-19. (2018, December 31). Retrieved from https://www.chronicle.com/interactives/tuition-and-fees

References Chronicle of Higher Education *, December 31, 2018.

 

 

** Soultion **

gf_density(~INSTATE_TUITION, data=Tuition,title=”Instate Tuition at all Four Year instittions”)

 

Instate Tuition at all Four Year instittions

 

4e−05

 

 

 

 

3e−05

 

 

 

 

density
2e−05

 

 

 

 

1e−05

 

 

 

 

0e+00

0200004000060000

INSTATE_TUITION

 

Figure 2.14: Density Plot for Instate Tuition Levels at all Four-Year Colleges**

gf_density(~INSTATE_TUITION|TYPE, data=Tuition,title=”Instate Tuition at all Four Year instittions”)

The distribution is skewed right, with no gaps. Most institutions in state is less than $ 20,000 per year though some go as high as $ 60,00 per year. When separated by public versus private and for profit, most public are much less than

$ 20,000 per year while private four year cost around $ 30,000 per year, and for profit are around $ 20,000 per year.

There are other types of graphs for quantitative data. They will be explored in the next section.

 

Homework

• The weekly median incomes of males and females for specific occupations, are given in table #2.2.3 (CPS News Releases. (n.d.). Retrieved July 8, 2019, from https://www.bls.gov/cps/). Create a density plot for males and females. Discuss any findings from the graph. Note: to put two graphs on the same axis, type %>% at the end of the first command and

 

Instate Tuition at all Four Year instittions

 

 

 

 

For_profit_4_year
Private_4_year
Public_4 year
0.00015

 

 

 

 

 

density
0.00010

 

 

 

 

 

0.00005

 

 

 

 

 

0.00000

0200004000060000 0200004000060000 0200004000060000

INSTATE_TUITION

 

Figure 2.15: Density Plot for Instate Tuition Levels at all Four-Year Colleges**

 

 

then type the command for the second graph on the next line. Also, use fill=“pick a color” in the command to plot the graphs with different colors so the two graphs can be easier to distinguish.

table #2.2.3: Weekly median wages for certain occupations

Wages<- read.csv( “https://krkozak.github.io/MAT160/wages.csv”)head(Wages)

 

##Occupation

## 1 Management, professional, and related occupations ## 2 Management, business, and financial operations occupations ## 3Management occupations

## 4Chief executives

## 5General and operations managers

## 6Legislators

##Numworkers median_wage male_worker male_wage

## 1	48808	1246	23685	1468
## 2	19863	1355	10668	1537
## 3	13477	1429	7754	1585
## 4	1098	2291	790	2488

## 593913386561427

 

 

## 614NA10NA

##female_worker female_wage

##	1	25123	1078
##	2	9195	1168
##	3	5724	1236
##	4	307	1736
##	5	283	1139
##	6	4	NA

Code book for Data Frame Wages

Description Median weekly earnings of full-time wage and salary workers by detailed occupation and sex. The Current Population Survey (CPS) is a monthly survey of households conducted by the Bureau of Census for the Bureau of Labor Statistics. It provides a comprehensive body of data on the labor force, employ- ment, unemployment, persons not in the labor force, hours of work, earnings, and other demographic and labor force characteristics.

Format

This data frame contains the following columns:

Occupation: Occupations of workers.

Numworkers: The number of workers in each occupation (in thousands of work- ers)

median_wage: Median weekly wage ($)

male_worker: number of male workers (in thousands of workers) male_wage: Median weekly wage of male workers ($) female_worker: number of female workers (in thousands of workers) female_wage: Median weekly wage of female workers ($)

Source CPS News Releases. (n.d.). Retrieved July 8, 2019, from https://www. bls.gov/cps/

References Current Population Survey (CPS) retrieved July 8, 2019.

• The density of people per square kilometer for certain countries is in table #2.2.4 (World Bank, 2019). Create density plot of density in 2018 for just Sub-Saharan Africa. Describe what story the graph tells.

Table #2.2.4: Data of Density of People per Square Kilometer

Density<- read.csv( “https://krkozak.github.io/MAT160/density.csv”)head(Density)

##Country_Name Country_CodeRegion ## 1ArubaABW Latin America & Caribbean

 

## 2AfghanistanAFGSouth Asia## 3AngolaAGOSub-Saharan Africa## 4AlbaniaALBEurope & Central Asia## 5AndorraANDEurope & Central Asia## 6Arab WorldARB##IncomeGroupy1961y1962y1963

 

 

 

 

 

 

##	1	High		income	307.988889		312.361111		314.972222
##	2	Low		income	14.044987		14.323808		14.617537
##	3	Lower middle		income	4.436891		4.498708		4.555593
##	4	Upper middle		income	60.576642		62.456898		64.329234
##	5	High		income	30.585106		32.702128		34.919149
##	6				8.430860		8.663154		8.903441
##	y1964			y1965		y1966		y1967		y1968
##	1	316.844444	318.666667			320.638889		322.527778		324.366667
##	2	14.926295	15.250314			15.585020		15.929795		16.293023
##	3	4.600180	4.628676			4.637213		4.631622		4.629544
##	4	66.209307	68.058066			69.874927		71.737153		73.805547
##	5	37.168085	39.465957			41.802128		44.165957		46.574468
##	6	9.152526	9.410965			9.679951		9.959490		10.247580
##		y1969	y1970			y1971		y1972		y1973
##	1	326.255556	328.127778			330.222222		332.444444		334.683333
##	2	16.686236	17.114913			17.577191		18.060863		18.547565
##	3	4.654892	4.724765			4.845413		5.012073		5.211328
##	4	75.974270	77.937190			79.848650		81.865912		83.823066
##	5	49.059574	51.651064			54.380851		57.217021		60.068085
##	6	10.541383	10.839409			11.140162		11.445801		11.762925
##		y1974	y1975			y1976		y1977		y1978
##	1	336.266667	336.983333			336.588889		335.366667		333.905556
##	2	19.013188	19.436265			19.825220		20.174779		20.435006
##	3	5.423422	5.634074			5.839022		6.042941		6.249063
##	4	85.770949	87.767555			89.727226		91.735255		93.659343
##	5	62.808511	65.329787			67.610638		69.725532		71.780851
##	6	12.100336	12.464221			12.856964		13.276051		13.716559
##		y1979	y1980			y1981		y1982		y1983
##	1	333.222222	333.866667			336.483333		340.805556		345.561111
##	2	20.542009	20.458461			20.175341		19.732451		19.204316
##	3	6.463517	6.690695			6.930654		7.181319		7.442124
##	4	95.541314	97.518139			99.491095		101.615985		103.794161
##	5	74.080851	76.738298			79.787234		83.221277		86.951064
##	6	14.171137	14.634158			15.103942		15.581254		16.065812
##		y1984	y1985			y1986		y1987		y1988
##	1	349.088889	350.144444			348.022222		343.516667		339.327778
##	2	18.693582	18.286015			17.976563		17.774920		17.795553
##	3	7.712163	7.990693			8.277943		8.574035		8.877878
##	4	106.001058	108.202993			110.315146		112.540329		114.683796
##	5	90.863830	94.893617			98.972340		103.095745		107.306383

 

 

##	6	16.557944	17.057705		17.563945		18.075438 18.592082
##		y1989	y1990		y1991		y1992y1993
##	1	339.066667	345.272222		359.011111		379.08333		402.80000
##	2	18.179820	19.012205		20.370396		22.18783		24.22664
##	3	9.188078	9.503799		9.825059		10.15270		10.48773
##	4	117.808139	119.946788		119.225912		118.50507		117.78420
##	5	111.591489	115.976596		120.576596		125.29362		129.72553
##	6	19.114029	19.817110		20.358106		20.73408		21.29364
##		y1994	y1995		y1996		y1997		y1998
##	1	426.11111	446.24444	462.22222		474.72778		484.87222
##	2	26.15527	27.74049	28.87822		29.64974		30.23277
##	3	10.83159	11.18570	11.55107		11.92875		12.32021
##	4	117.06336	116.34248	115.62164		114.90077		114.17993
##	5	133.35532	135.85106	136.93617		136.86596		136.47234
##	6	21.84602	22.52760	23.05216		23.57027		24.08237
##		y1999	y2000	y2001		y2002		y2003
##	1	494.47222	504.73889	516.10000		527.73333		538.98333
##	2	30.89612	31.82911	33.09590		34.61810		36.27251
##	3	12.72709	13.15110	13.59249		14.05263		14.53556
##	4	113.45905	112.73821	111.68515		111.35073		110.93489
##	5	136.95745	139.12766	143.27872		149.04043		155.70638
##	6	24.60020	25.12980	25.67166		26.22642		26.80081
##		y2004	y2005	y2006		y2007		y2008
##	1	548.53889	555.72778	560.18889		562.34444		563.10000
##	2	37.87440	39.29522	40.48808		41.51049		42.46282
##	3	15.04624	15.58803	16.16259		16.76856		17.40245
##	4	110.47223	109.90828	109.21704		108.39478		107.56620
##	5	162.22128	167.80213	172.32553		175.92340		178.42979
##	6	27.40153	28.03371	28.69994		29.39751		30.11889
##		y2009	y2010	y2011		y2012		y2013
##	1	563.63889	564.82778	566.92222		569.77778		573.10556
##	2	43.49296	44.70408	46.13150		47.73056		49.42804
##	3	18.05910	18.73446	19.42782		20.13951		20.86771
##	4	106.84376	106.31463	106.02901		105.85405		105.66029
##	5	179.70851	179.67872	178.18511		175.37660		171.85957
##	6	30.85858	31.59402	32.33012		33.06767		33.80379
##		y2014	y2015	y2016		y2017		y2018
##	1	576.52222	579.67222	582.62222		585.36667		588.02778
##	2	51.11478	52.71207	54.19711		55.59599		56.93776
##	3	21.61047	22.36655	23.13506		23.91654		24.71305
##	4	105.44175	105.13515	104.96719		104.87069		104.61226
##	5	168.53830	165.98085	164.46170		163.83191		163.84255
##	6	34.53398	35.25690	35.96876		36.66980		37.37237

Code book for Data Frame Density

Description Population density of all countries in the world

 

 

Format

This data frame contains the following columns:

Country_Name: The name of countries or regions around the world Country_Code: The 3 letter code for a country or region

Region: World Banks classification of where the country is in the world

Incomegroup: World Banks classification of what income level the country is considered to be

y1961-y2018: population density for the years 1961 through 2018, people per sq. km of land area, population density is midyear population divided by land area in square kilometers. Population is based on the de facto definition of population, which counts all residents regardless of legal status or citizenship– except for refugees not permanently settled in the country of asylum, who are generally considered part of the population of their country of origin. Land area is a country’s total area, excluding area under inland water bodies, national claims to continental shelf, and exclusive economic zones. In most cases the definition of inland water bodies includes major rivers and lakes.

Source Population density (people per sq. km of land area). (n.d.). Retrieved July 9, 2019, from https://data.worldbank.org/indicator/EN.POP.DNST

References Food and Agriculture Organization and World Bank population estimates.

Since the Density data frame is for all countries, a new data frame must be created with just Su-Saharan Africa. This is created by using the following command

Africa<- Density%>%filter(Region==”Sub-Saharan Africa”)head(Africa)

##Country_Name Country_CodeRegion ## 1AngolaAGO Sub-Saharan Africa

## 2BurundiBDI Sub-Saharan Africa

## 3BeninBEN Sub-Saharan Africa

## 4Burkina FasoBFA Sub-Saharan Africa

## 5BotswanaBWA Sub-Saharan Africa ## 6 Central African RepublicCAF Sub-Saharan Africa ##IncomeGroupy1961y1962y1963 ## 1 Lower middle income4.43689104.49870784.5555932

## 2Low income 111.0762461 113.2134346 115.4371885

## 3Low income 21.8682778 22.1966655 22.5510731

## 4Low income 17.8895468 18.1298465 18.3765387

## 5 Upper middle income0.90463710.92421080.9452208

 

 

##14.60017974.62867574.6372134.6316224.629544##2117.8461838120.4976246123.461449126.682944129.942640##322.933354023.344767723.78644024.25777824.756917##418.636293918.913998519.21185319.52857819.861261##50.96672670.98811431.0092351.0306351.053318##62.58213102.63203632.6855102.7421462.799759##y1969y1970y1971y1972y1973##14.6548924.7247654.8454135.0120735.211328##2132.940187135.477959137.460942139.005685140.386527##325.28078225.82777626.39741026.99154827.613294##420.20531420.55774920.91879021.29083721.675742##51.0786441.1076091.1404851.1770901.217356##62.8554062.9072272.9543772.9981413.041595##y1974y1975y1976y1977y1978##15.4234225.6340745.8390226.0429416.249063##2141.994977144.115265146.840771150.095210153.787617##328.26722228.95676729.68404630.44908731.251667##422.07617322.49468222.93142223.38792023.869952##51.2611161.3081271.3586351.4125401.468895##63.0890043.1435473.2055833.2744533.351092##y1979y1980y1981y1982y1983##16.4635176.6906956.9306547.1813197.442124##2157.758333161.888551166.141744170.550000175.137578##332.09051132.96528033.87839734.83251235.827856##424.38470824.93729225.53055626.16321326.830793##51.5264321.5842961.6417131.6990011.757680##63.4363493.5303803.6348553.7486483.865801##y1984y1985y1986y1987y1988##17.7121637.9906938.2779438.5740358.877878##2179.949494185.001441190.293731195.760826201.273287##336.86430537.94342939.06089040.22049541.440688##427.52646928.24527428.98645529.75172930.542050##51.8199831.8872871.9602692.0378422.117529##63.9782694.0806594.1698954.2486764.324333##y1989y1990y1991y1992y1993##19.1880789.5037999.82505910.15269610.487727##2206.661565211.797391216.702726221.400506225.780880##342.74579644.15125945.66778147.28452548.969165##431.35900232.20407233.07779233.98067634.914020##52.1959032.2704922.3403072.4060032.468742##64.4074194.5053364.6205484.7501304.889642##y1994y1995y1996y1997y1998##110.83159311.18569511.55107011.92874812.320206##2229.710553233.140304235.985631238.400701240.870794
## 6Low income2.44962282.49110732.5351857 ##y1964y1965y1966y1967y1968

 

 

##	3	50.675949	52.372810	54.046284	55.708044	57.380853
##	4	35.879342	36.878209	37.912080	38.982259	40.090365
##	5	2.530410	2.592370	2.655109	2.718093	2.780555
##	6	5.032288	5.172969	5.310336	5.445497	5.578818
##		y1999	y2000	y2001	y2002	y2003
##	1	12.727095	13.151097	13.592487	14.052633	14.535557
##	2	244.046885	248.398403	254.110008	261.063590	269.048053
##	3	59.099840	60.889952	62.759250	64.698421	66.695238
##	4	41.237942	42.426689	43.657116	44.930921	46.252270
##	5	2.841325	2.899677	2.954984	3.007856	3.060360
##	6	5.711281	5.843570	5.974539	6.103130	6.230025
##		y2004	y2005	y2006	y2007	y2008
##	1	15.046238	15.588034	16.162590	16.768559	17.402450
##	2	277.713902	286.793692	296.255802	306.160981	316.436994
##	3	68.730082	70.789509	72.870672	74.980427	77.127714
##	4	47.626349	49.056762	50.545234	52.090720	53.690515
##	5	3.115288	3.174489	3.239476	3.309264	3.380162
##	6	6.356344	6.482362	6.610275	6.738595	6.859556
##		y2009	y2010	y2011	y2012	y2013
##	1	18.059101	18.734456	19.427818	20.139513	20.867715
##	2	327.011994	337.834969	348.847586	360.046262	371.506581
##	3	79.325186	81.582645	83.902359	86.282795	88.724619
##	4	55.340270	57.036612	58.778914	60.567420	62.400493
##	5	3.446964	3.506264	3.556194	3.598805	3.639363
##	6	6.962703	7.041587	7.092741	7.121280	7.139783
##		y2014	y2015	y2016	y2017	y2018
##	1	21.610475	22.366553	23.135064	23.916538	24.713052
##	2	383.344899	395.639797	408.411137	421.613084	435.178271
##	3	91.227758	93.791699	96.417763	99.106101	101.853920
##	4	64.276378	66.193801	68.151966	70.150892	72.191283
##	5	3.685378	3.742022	3.811240	3.890967	3.977425
##	6	7.165840	7.212382	7.283841	7.377489	7.490412

• The Affordable Care Act created a market place for individuals to pur- chase health care plans. In 2014, the premiums for a 27 year old for the different levels health insurance are given in table #2.2.5 (”Health insur- ance marketplace,” 2013). Create a density plot of bronze_lowest, then silver_lowest, and gold_lowest all on the same aces. Use %>% at the end of each command. Describe the story the graphs tells.

Table #2.2.5: Data of Health Insurance Premiums

Insurance<- read.csv( “https://krkozak.github.io/MAT160/insurance.csv”)head(Insurance)

 

##state average_QHP bronze_lowest silver_lowest gold_lowest

 

 

## 1	AK	34	254	312	401
## 2	AL	7	162	200	248
## 3	AR	28	181	231	263
## 4	AZ	106	141	164	187
## 5	DE	19	203	234	282
## 6	FL	102	169	200	229

##catastrophic second_silver_pretax second_silver_posttax

##	1	236	312		107
##	2	138	209		145
##	3	135	241		145
##	4	107	166		145
##	5	137	237		145
##	6	132	218		145
##lowest_bronze_posttax silver_family_pretax
##	1	48		1131
##	2	98		757
##	3	85		873
##	4	120		600
##	5	111		859
##	6	96		789
##silver_family_posttax bronze_family_posttax
##	1	205		0
##	2	282		112
##	3	282		64
##	4	282		192
##	5	282		158
##	6	282		104

Code book for Data Frame Insurance

Description The Affordable Care Act created a market place for individuals to purchase health care plans.The data is from 2014.

Format

This data frame contains the following columns:

state: state of insured.

average_QHP: The number of qualified health plans

bronze_lowest: premium for the lowest bronze level of insurance for a single person ($)

silver_lowest: premium for the lowest silver level of insurance for a single person ($)

gold_lowest: premium for the lowest gold level of insurance for a single person ($)

 

 

catastrophic: premium for the catastrophic level of insurance for a single person ($)

second_silver_pretax: premium for the second silver level of insurance for a single person pretax ($)

second_silver_posttax: premium for the second silver level of insurance for a single person posttax ($)

second_bronze_posttax: premium for the lowest bronze level of insurance for a single person posttax ($)

silver_family_pretax: premium for the silver level of insurance for a family pretax ($)

silver_family_posttax: premium for the silver level of insurance for a family posttax ($)

bronze_family_posttax: premium for the bronze level of insurance for a family posttax ($)

Source Health Insurance Market Place Retrieved from website: http://aspe. hhs.gov/health/reports/2013/marketplacepremiums/ib_premiumslandscape. pdf premiums for 2014.

References Department of Health and Human Services, ASPE. (2013). Health insurance marketplace

• Students in a statistics class took their first test. The following are the scores they earned. Create a density plot for grades. Describe the shape of the distribution.

Table #2.2.6: Data of Test 1 Grades

Firsttest_1<- read.csv( “https://krkozak.github.io/MAT160/firsttest_1.csv”)head(Firsttest_1)

##grades

## 1	80
## 2	79
## 3	89
## 4	74
## 5	73
## 6	67

• Students in a statistics class took their first test. The following are the scores they earned. Create a density plot for grades. Describe the shape of the distribution. Compare to the graph in question 4.

Table #2.2.7: Data of Test 1 Grades

 

 

Firsttest_2<- read.csv( “https://krkozak.github.io/MAT160/firsttest_2.csv”)head(Firsttest_2)

## grades

## 1	67
## 2	67
## 3	76
## 4	47
## 5	85
## 6	70

 

 

 

 

Other Graphical Representations of Data

There are many other types of graphs. Some of the more common ones are the point plot (scatter plot), and a time-series plot. There are also many different graphs that have emerged lately for qualitative data. Many are found in pub- lications and websites. The following is a description of the point plot (scatter plot), and the time-series plot.

Point Plots or Scatter Plot

Sometimes you have two different variables and you want to see if they are related in any way. A scatter plot helps you to see what the relationship would look like. A scatter plot is just a plotting of the ordered pairs.

 

Example: Scatter Plot**

Is there a relationship between systolic blood pressure and weight? To answer this question some data is needed. The data frame NHANES contains this data, but given the size of the data frame, it may be not be very useful to look at the graph of all the data. It makes sense to take a sample form the data frame. A random sample is the better type of sample to take. Once the sample is taken, then a scatter plot can be created. The R studio command for a scatter plot is

gf_point(response variable ~ explanatory variable, data= Data Frame)

 

Solution:

Table #2.3.1: Random sample of size 100 from the data frame NHANES

sample_NHANES <- NHANES%>%

 

 

sample_n(size = 100)head(sample_NHANES)

 

##	#	A tibble: 6 x 76
##		ID SurveyYr Gender	Age	AgeDecade AgeMonths		Race1
##		<int> <fct><fct>	<int>	<fct><int>		<fct>
##	1	63223 2011_12 male	59	” 50-59″	NA	White
##	2	66721 2011_12 female	47	” 40-49″	NA	Other
##	3	70807 2011_12 female	22	” 20-29″	NA	Mexi~
##	4	52460 2009_10 female	10	” 10-19″	122	White
##	5	62784 2011_12 male	31	” 30-39″	NA	Hisp~
##	6	63418 2011_12 female	40	” 40-49″	NA	White
## ##	# #	… with 69 more variables: Race3 <fct>, Education <fct>, MaritalStatus <fct>, HHIncome <fct>, HHIncomeMid <int>,
##	#	Poverty <dbl>, HomeRooms <int>, HomeOwn <fct>,
##	#	Work <fct>, Weight <dbl>, Length <dbl>, HeadCirc <dbl>,
##	#	Height <dbl>, BMI <dbl>, BMICatUnder20yrs <fct>,
##	#	BMI_WHO <fct>, Pulse <int>, BPSysAve <int>,
##	#	BPDiaAve <int>, BPSys1 <int>, BPDia1 <int>,
##	#	BPSys2 <int>, BPDia2 <int>, BPSys3 <int>, BPDia3 <int>,
##	#	Testosterone <dbl>, DirectChol <dbl>, TotChol <dbl>,
##	#	UrineVol1 <int>, UrineFlow1 <dbl>, UrineVol2 <int>,
##	#	UrineFlow2 <dbl>, Diabetes <fct>, DiabetesAge <int>,
##	#	HealthGen <fct>, DaysPhysHlthBad <int>,
##	#	DaysMentHlthBad <int>, LittleInterest <fct>,
##	#	Depressed <fct>, nPregnancies <int>, nBabies <int>,
##	#	Age1stBaby <int>, SleepHrsNight <int>,
##	#	SleepTrouble <fct>, PhysActive <fct>,
##	#	PhysActiveDays <int>, TVHrsDay <fct>, CompHrsDay <fct>,
##	#	TVHrsDayChild <int>, CompHrsDayChild <int>,
##	#	Alcohol12PlusYr <fct>, AlcoholDay <int>,
##	#	AlcoholYear <int>, SmokeNow <fct>, Smoke100 <fct>,
##	#	Smoke100n <fct>, SmokeAge <int>, Marijuana <fct>,
##	#	AgeFirstMarij <int>, RegularMarij <fct>,
##	#	AgeRegMarij <int>, HardDrugs <fct>, SexEver <fct>,
##	#	SexAge <int>, SexNumPartnLife <int>,
##	#	SexNumPartYear <int>, SameSex <fct>,
##	#	SexOrientation <fct>, PregnantNow <fct>

Preliminary: State the explanatory variable and the response variable Let x=explanatory variable = Weight y=response variable = BPSys1

gf_point(BPSys1~Weight, data=sample_NHANES)

 

Looking at the graph, it appears that there is a linear relationship between weight and systolic blood pressure though it looks somewhat weak. It also

 

 

 

 

 

 

 

 

 

180

 

 

 

 

 

BPSys1
150

 

 

 

 

 

120

 

 

 

 

 

90

50100150

Weight

 

Figure 2.16: Scatter Plot of Blood Pressure versus Weight

 

appears to be a positive relationship, thus as weight increases, the systolic blood pressure increases.

Time-Series

A time-series plot is a graph showing the data measurements in chronological order, the data being quantitative data. For example, a time-series plot is used to show profits over the last 5 years. To create a time-series plot on R Studio, use the command

gf_line(response variable ~ explanatory variable, data=Data Frame)

 

The purpose of a time-series graph is to look for trends over time. Caution, you must realize that the trend may not continue. Just because you see an increase, doesn’t mean the increase will continue forever. As an example, prior to 2007, many people noticed that housing prices were increasing. The belief at the time was that housing prices would continue to increase. However, the housing bubble burst in 2007, and many houses lost value, and haven’t recovered.

 

Example: Time-Series Plot**

The bank assets (in billions of Australia dollars (AUD)) of the Reserve Bank of Australia (RBA) and other financial organizations for the time period of Septem- ber 1 1969, through March 1 2019, are contained in table #2.3.2 (Reserve Bank

 

 

of Australia, 2019). Create a time-series plot of the total assets of Authorized Deposit-taking Institutions (ADIs) and interpret any findings.

Table #2.3.2: Data of Date versus RBA Assets

Australian<- read.csv( “https://krkozak.github.io/MAT160/Australian_financial.csv”)head(Australian)

 

##Date Day Assets_RBA Assets_ADIs_Banks
##	1	Sep-69	0	2.7		NA
##	2	Dec-69	90	2.9		NA
##	3	Mar-70	180	3.0		NA
##	4	Jun-70	270	3.0		NA
##	5	Sep-70	360	3.0		NA
##	6	Dec-70	450	3.0		NA
##Assets_ADIs_Building Assets_ADIs_CU Assets_ADIs_Total
##	1	NA				NA	NA
##	2	NA				NA	NA
##	3	NA				NA	NA
##	4	NA				NA	NA
##	5	NA				NA	NA
##	6	NA				NA	NA
##Assets_RFCs_MM Assets_RFCs_Finance Assets_RFCs_Total
##	1	NA			NA		NA
##	2	NA			NA		NA
##	3	NA			NA		NA
##	4	NA			NA		NA
##	5	NA			NA		NA
##	6	NA			NA		NA
## ##	1	Assets_Life.offices Assets_Life_funds NANA					Assets_Life_Total NA
##	2	NA				NA	NA
##	3	NA				NA	NA
##	4	NA				NA	NA
##	5	NA				NA	NA
##	6	NA				NA	NA
##		Assets_Other_Public_trusts Assets_Other_Cash_trusts
##	1	NANA
##	2	NANA
##	3	NANA
##	4	NANA
##	5	NANA
##	6	NANA
##		Assets_Other_Common_funds Assets_Others_Friendly
##	1	NANA
##	2	NANA

 

 

## 3	NA	NA
## 4	NA	NA
## 5	NA	NA
## 6	NA	NA

##Assets_Other_General_insurance Assets_Other_vehicles ## 1NANA

## 2NANA

## 3NANA

## 4NANA

## 5NANA

## 6NANA

##Assets_Unconsolidated

##	1	NA
##	2	NA
##	3	NA
##	4	NA
##	5	NA
##	6	NA

Code book for Data frame Australian

Description The data is a range of economic and financial data produced by the Reserve Bank of Australia and other organizations.

Format

This data frame contains the following columns:

Date: quarters from September 1 1969 to March 1, 2019

Day: The number of days since September 1, 1969 using 90 days between starts of a quarter. This column is to make it easier to graph in R Studio, and has no other purpose.

Assets_RBA: The assets for the Royal Bank of Australia

Assets_ADIs_Banks: The assets for Authorized Deposit-taking Institutions (ADIs), Banks

Assets_ADIs_Building: The assets for Authorized Deposit-taking Institutions (ADIs), Building societies

Assets_ADIs_CU: The assets for Authorized Deposit-taking Institutions (ADIs), Credit Unions

Assets_ADIs_Total: The assets for Authorized Deposit-taking Institutions (ADIs), total

Assets_RFCs_MM: The assets for Registered Financial Corporations (RFCs), Money Market Corporations

 

 

Assets_RFCs_Finance:The assets for Registered Financial Corporations (RFCs), Finance companies and general financiers

Assets_RFCs_Total: The assets for Registered Financial Corporations (RFCs) total

Assets_Life offices: The Assets of Life offices and superannuation funds; Life insurance offices

Assets_Life_funds: The Assets of Life offices and superannuation funds; Super- annuation funds

Assets_Life_Total: The Assets of Life offices and superannuation; Total

Assets_Other_Public_trusts: The Assets of Other managed funds; Public unit trusts

Assets_Other_Cash_trusts: The Assets of Other managed funds; Cash man- agement trusts

Assets_Other_Common_funds: The Assets of Other managed funds; Common funds

Assets_Others_Friendly: The Assets of Other managed funds; Friendly soci- eties

Assets_Other_General_insurance: The Assets of Other financial institutions; General insurance offices

Assets_Other_vehicles: The Assets Other financial institutions; Securitisation vehicles

Assets_Unconsolidated: The Assets of Unconsolidated; Statutory funds of life insurance offices; Superannuation

Source Reserve Bank of Australia. (2019, May 13). Statistical Tables. Re- trieved July 10, 2019, from https://www.rba.gov.au/statistics/tables/

References Reserve Bank of Australia and other organizations

Solution: variable, x=total assets of Authorized Deposit-taking Institutions (ADIs)

Looking at the code book, one can see that the variable Assets_ADIs_Total is the variable in the data frame that is of interest here. With a time series plot, the other variable is time. In this case the variable in the data frame that represents time is Date. The problem with Date is that the units are every quarter. This is not easily interpreted by R Studio, so a column was created called Day. From the code book, this is the number of days since September 1, 1969 using 90 days between starts of a quarter. Even though this isn’t perfect, it will work for determining trends. So create a time series plot of Assets_ADIs_Total versus Day. The command is:

 

 

gf_line(Assets_ADIs_Total~Day, data=Australian, title=”Total Assets of Authorized Deposit-taking

 

Total Assets of Authorized Deposit−taking Institutions (ADIs)

 

 

 

4000

 

 

 

 

Assets_ADIs_Total
3000

 

 

 

 

2000

 

 

 

 

1000

 

 

 

 

050001000015000

Day

 

Figure 2.17: Time-Series Graph of Total Assets of ADIs versus Time

 

From the graph, total assets of Authorized Deposit-taking Institutions (ADIs) appear to be increasing with a slight dip around 14000 days since September 1, 1969. That would be around the year 2008 (14000 days /360 days per year + 1969).

Be careful when making a graph. If the vertical axis doesn’t start at 0, then the change can look much more dramatic than it really is. For a graph to be useful to the reader, it needs to have a title that explains what the graph contains, the axes should be labeled so the reader knows what each axes represents, each axes should have a scale marked, and it is best if the vertical axis contains 0 to show the relationship.

 

Homework

• When an anthropologist finds skeletal remains, they need to figure out the height of the person. The height of a person (in cm) and the length of one of their metacarpal bone (in cm) were collected and are in table #2.3.3 (Prediction of height, 2013). Create a scatter plot of length and height and state if there is a relationship between the height of a person and the length of their metacarpal.

 

Table #2.3.3: Data of Metacarpal versus Height

Metacarpal<- read.csv( “https://krkozak.github.io/MAT160/metacarpal.csv”)head(Metacarpal)

##length height

## 1	45	171
## 2	51	178
## 3	39	157
## 4	41	163
## 5	48	172
## 6	49	183

Code book for Data frame Metacarpal

Description When anthropologists analyze human skeletal remains, an impor- tant piece of information is living stature. Since skeletons are commonly based on statistical methods that utilize measurements on small bones. The following data was presented in a paper in the American Journal of Physical Anthropology to validate one such method.

Format

This data frame contains the following columns:

length: length of Metacarpal I bone in cm height: stature of skeleton in cm

Source Prediction of Height from Metacarpal Bone Length. (n.d.). Retrieved July 9, 2019, from http://www.statsci.org/data/general/stature.html

References Musgrave, J., and Harneja, N. (1978). The estimation of adult stature from metacarpal bone length. Amer. J. Phys. Anthropology 48, 113- 120.

Devore, J., and Peck, R. (1986). Statistics. The Exploration and Analysis of Data. West Publishing, St Paul, Minnesota.

• Table #2.3.4 contains the value of the house and the amount of rental income in a year that the house brings in (Capital and rental 2013). Create a scatter plot and state if there is a relationship between the value of the house and the annual rental income.

Table #2.3.4: Data of House Value versus Rental

House<- read.csv( “https://krkozak.github.io/MAT160/house.csv”)head(House)

##capital rental ## 1615006656

 

 

## 2	67500	6864
## 3	75000	4992
## 4	75000	7280
## 5	76000	6656
## 6	77000	4576

Code book for Data frame House

Description The data show the capital value and annual rental value of do- mestic properties in Auckland in 1991.

Format

This data frame contains the following columns:

Capital: Selling price of house in Australian dollar (AUD) rental: rental price of a house in Australian dollar (AUD)

Source Capital and rental values of Auckland properties. (2013, September 26). Retrieved from http://www.statsci.org/data/oz/rentcap.html

References Lee, A. (1994) Data Analysis: An introduction based on R. Auck- land: Department of Statistics, University of Auckland. Data courtesy of Sage Consultants Ltd.

• The World Bank collects information on the life expectancy of a person in each country (”Life expectancy at,” 2013) and the fertility rate per woman in the country (”Fertility rate,” 2013). The data for countries for the year 2011 are in table #2.3.5. Create a scatter plot of the data and state if there appears to be a relationship between life expectancy and the number of births per woman in 2011.

Table #2.3.5: Data of Life Expectancy versus Fertility Rate

Fertility<- read.csv( “https://krkozak.github.io/MAT160/fertility.csv”)head(Fertility)

##country lifexp_2011 fertilrate_2011

##	1	Macao SAR, China	79.91	1.03
##	2	Hong Kong SAR, China	83.42	1.20
##	3	Singapore	81.89	1.20
##	4	Hungary	74.86	1.23
##	5	Korea, Rep.	80.87	1.24
##	6	Romania	74.51	1.25

## 177.620.9475.281.69## 280.881.0477.381.27## 378.05NA76.031.87## 471.251.3269.321.84
##lifexp_2000 fertilrate_2000 lifexp_1990 fertilrate_1990

 

 

## 5	75.86	1.47	71.29	1.59
## 6	71.16	1.31	69.74	1.84
Code book for Data frame Fertility

Description Data is from the World Bank on the life expectancy of countries and the fertility rates in those countries.

Format

This data frame contains the following columns:

Country: Countries in the World

lifexp_2011: Life expectancy of a person born in 2011 fertilrate_2011: Fertility rate in the country in 2011 lifexp_2000: Life expectancy of a person born in 2000 fertilrate_2000: Fertility rate in the country in 2000 lifexp_1990: Life expectancy of a person born in 1990 fertilrate_1990: Fertility rate in the country in 1990

Source Life expectancy at birth. (2013, October 14). Retrieved from http:

//data.worldbank.org/indicator/SP.DYN.LE00.IN

References Data from World Bank, Life expectancy at birth, total (years)

• The World Bank collected data on the percentage of gross domestic prod- uct (GDP) that a country spends on health expenditures (Current health expenditure (% of GDP), 2019), the fertility rate of the country (Fertility rate, total (births per woman), 2019), and the percentage of woman re- ceiving prenatal care (Pregnant women receiving prenatal care (%), 2019). The data for the countries where this information is available in table #2.3.6. Create a scatter plot of the health expenditure and percentage of woman receiving prenatal care in the year 2014, and state if there appears to be a relationship between percentage spent on health expenditure and the percentage of woman receiving prenatal care.

Table #2.3.6: Data of Prenatal Care versus Health Expenditure

Fert_prenatal<-read.csv( “https://krkozak.github.io/MAT160/fertility_prenatal.csv”)head(Fert_prenatal)

## Country.Name Country.CodeRegion ## 1 Angola AGO Sub-Saharan Africa ## 2 Armenia ARM Europe & Central Asia ## 3 Belize BLZ Latin America & Caribbean ## 4 Cote d’Ivoire CIV Sub-Saharan Africa ## 5 Ethiopia ETH Sub-Saharan Africa

 

## ##6Guinea IncomeGroupGIN f1960 f1961Sub-Saharan Africa f1962 f1963 f1964 f1965##1Lowermiddleincome7.4787.5247.5637.5927.6117.619##2Uppermiddleincome4.7864.6704.5214.3454.1503.950##3Uppermiddleincome6.5006.4806.4606.4406.4206.400##4Lowermiddleincome7.6917.7207.7507.7817.8117.841##5Lowincome6.8806.8776.8756.8726.8676.864##6Lowincome6.1146.1276.1386.1476.1546.160

 

 

 

 

 

 

 

 

##	f1966		f1967	f1968	f1969	f1970	f1971	f1972	f1973	f1974
##	1	7.618	7.613	7.608	7.604	7.601	7.603	7.606	7.611	7.614
##	2	3.758	3.582	3.429	3.302	3.199	3.114	3.035	2.956	2.875
##	3	6.379	6.358	6.337	6.316	6.299	6.288	6.284	6.285	6.287
##	4	7.868	7.893	7.912	7.927	7.936	7.941	7.942	7.939	7.929
##	5	6.867	6.880	6.903	6.937	6.978	7.020	7.060	7.094	7.121
##	6	6.168	6.177	6.189	6.205	6.225	6.249	6.277	6.306	6.337
##		f1975	f1976	f1977	f1978	f1979	f1980	f1981	f1982	f1983
##	1	7.615	7.609	7.594	7.571	7.540	7.504	7.469	7.438	7.413
##	2	2.792	2.712	2.641	2.582	2.538	2.510	2.499	2.503	2.517
##	3	6.278	6.250	6.195	6.109	5.992	5.849	5.684	5.510	5.336
##	4	7.910	7.877	7.828	7.763	7.682	7.590	7.488	7.383	7.278
##	5	7.143	7.167	7.195	7.230	7.271	7.316	7.360	7.397	7.424
##	6	6.369	6.402	6.436	6.468	6.500	6.529	6.557	6.581	6.602
##		f1984	f1985	f1986	f1987	f1988	f1989	f1990	f1991	f1992
##	1	7.394	7.380	7.366	7.349	7.324	7.291	7.247	7.193	7.130
##	2	2.538	2.559	2.578	2.591	2.592	2.578	2.544	2.484	2.400
##	3	5.170	5.019	4.886	4.771	4.671	4.584	4.508	4.436	4.363
##	4	7.176	7.078	6.984	6.892	6.801	6.710	6.622	6.536	6.454
##	5	7.437	7.435	7.418	7.387	7.347	7.298	7.246	7.193	7.143
##	6	6.619	6.631	6.637	6.637	6.631	6.618	6.598	6.570	6.535
##		f1993	f1994	f1995	f1996	f1997	f1998	f1999	f2000	f2001
##	1	7.063	6.992	6.922	6.854	6.791	6.734	6.683	6.639	6.602
##	2	2.297	2.179	2.056	1.938	1.832	1.747	1.685	1.648	1.635
##	3	4.286	4.201	4.109	4.010	3.908	3.805	3.703	3.600	3.496
##	4	6.374	6.298	6.224	6.152	6.079	6.006	5.932	5.859	5.787
##	5	7.094	7.046	6.995	6.935	6.861	6.769	6.659	6.529	6.380
##	6	6.493	6.444	6.391	6.334	6.273	6.211	6.147	6.082	6.015
##		f2002	f2003	f2004	f2005	f2006	f2007	f2008	f2009	f2010
##	1	6.568	6.536	6.502	6.465	6.420	6.368	6.307	6.238	6.162
##	2	1.637	1.648	1.665	1.681	1.694	1.702	1.706	1.703	1.693
##	3	3.390	3.282	3.175	3.072	2.977	2.893	2.821	2.762	2.715
##	4	5.717	5.651	5.589	5.531	5.476	5.423	5.372	5.321	5.269
##	5	6.216	6.044	5.867	5.690	5.519	5.355	5.201	5.057	4.924
##	6	5.947	5.877	5.804	5.729	5.653	5.575	5.496	5.417	5.336
##		f2011	f2012	f2013	f2014	f2015	f2016	f2017	p1986	p1987
##	1	6.082	6.000	5.920	5.841	5.766	5.694	5.623	NA	NA
##	2	1.680	1.664	1.648	1.634	1.622	1.612	1.604	NA	NA

 

## 1NANANANANANANANANA## 2NANANANANANANANANA## 3NANANA96NANANANANA## 4NANANANANANA83.2NANA## 5NANANANANANANANANA## 6NANANANA57.6NANANANA
##32.6762.6422.6102.5782.5442.5102.475NANA##45.2165.1605.1015.0394.9764.9114.846NANA##54.7984.6774.5564.4374.3174.1984.081NANA##65.2565.1755.0945.0144.9344.8554.777NANA##p1988p1989p1990p1991p1992p1993p1994p1995p1996

 

 

 

 

 

 

 

 

 

 

 

##	p1997		p1998		p1999	p2000	p2001		p2002		p2003	p2004		p2005
##	1	NA	NA		NA	NA	65.6		NA		NA	NA		NA
##	2	82	NA		NA	92.4	NA		NA		NA	NA		93.0
##	3	NA	98		95.9	100.0	NA		98		NA	NA		94.0
##	4	NA	NA		84.3	87.6	NA		NA		NA	NA		87.3
##	5	NA	NA		NA	26.7	NA		NA		NA	NA		27.6
##	6	NA	NA		70.7	NA	NA		NA		84.3	NA		82.2
##		p2006	p2007		p2008	p2009	p2010		p2011		p2012	p2013		p2014
##	1	NA	79.8		NA	NA	NA		NA		NA	NA		NA
##	2	NA	NA		NA	NA	99.1		NA		NA	NA		NA
##	3	94.0	99.2		NA	NA	NA		96.2		NA	NA		NA
##	4	84.8	NA		NA	NA	NA		NA		90.6	NA		NA
##	5	NA	NA		NA	NA	NA		33.9		NA	NA		41.2
##	6	NA	88.4		NA	NA	NA		NA		85.2	NA		NA
##	p2015		p2016		p2017	p2018	e2000				e2001	e2002
##	1	NA	81.6		NA	NA	2.334435			5.483824		4.072288
##	2	NA	99.6		NA	NA	6.505224			6.536262		5.690812
##	3	97.2	97.2		NA	NA	3.942030			4.228792		3.864327
##	4	NA	93.2		NA	NA	5.672228			4.850694		4.476869
##	5	NA	62.4		NA	NA	4.365290			4.713670		4.705820
##	6	NA	84.3		NA	NA	3.697726			3.884610		4.384152
##	e2003				e2004	e2005			e2006		e2007			e2008
##	1	4.454100		4.757211		3.734836		3.366183			3.211438		3.495036
##	2	5.610725		8.227844		7.034880		5.588461			5.445144		4.346749
##	3	4.260178		4.091610		4.216728		4.163924			4.568384		4.646109
##	4	4.645306		5.213588		5.353556		5.808850			6.259154		6.121604
##	5	4.885341		4.304562		4.100981		4.226696			4.801925		4.280639
##	6	3.651081		3.365547		2.949490		2.960601			3.013074		2.762090
##		e2009		e2010		e2011		e2012			e2013		e2014
##	1	3.578677		2.736684		2.840603		2.692890			2.990929		2.798719
##	2	4.689046		5.264181		3.777260		6.711859			8.269840		10.178299
##	3	5.311070		5.764874		5.575126		5.322589			5.727331		5.652458
##	4	6.223329		6.146566		5.978840		6.019660			5.074942		5.043462
##	5	4.412473		5.466372		4.468978		4.539596			4.075065		4.033651
##	6	2.936868		3.067742		3.789550		3.503983			3.461137		4.780977

 

 

##e2015e2016 ## 1 2.950431 2.877825

## 2 10.117628 9.927321

## 3 5.884248 6.121374

## 4 5.262711 4.403621

## 5 3.975932 3.974016

## 6 5.827122 5.478273

Code book for Data frame Fert_prenatal

Description Data is from the World Bank on money spent on expenditure of countries and the percentage of woman receiving prenatal care in those coun- tries.

Format

This data frame contains the following columns:

Country.Name: Countries around the world

Country.Code: Three letter country code for countries around the world Region: Location of a country around the world as classified by the World Bank IncomeGroup: The income level of a country as classified by the World Bank f1960-f2017: Fertility rate of a country from 1960-2017

p1986-p2018: Percentage of woman receiving prenatal care in the country in 1986-2018

e200-2016: Expenditure amounts of the countries for medical care in 2000-2016 (% of GDP)

Source Fertility rate, total (births per woman). (n.d.). Retrieved July 8, 2019, from https://data.worldbank.org/indicator/SP.DYN.TFRT.IN Pregnant women receiving prenatal care (%). (n.d.). Retrieved July 9, 2019, from https:// data.worldbank.org/indicator/SH.STA.ANVC.ZS Current health expenditure (% of GDP). (n.d.). Retrieved July 9, 2019, from https://data.worldbank.org/ indicator/SH.XPD.CHEX.GD.ZS

References Data from World Bank, fertility rate, expenditure on health, and pregnant woman rate of prenatal care.

• The Australian Institute of Criminology gathered data on the number of deaths (per 100,000 people) due to firearms during the period 1983 to 1997 (”Deaths from firearms,” 2013). The data is in table #2.3.7. Create a time-series plot of the data and state any findings you can from the graph.

Table #2.3.7: Data of Year versus Number of Deaths due to Firearms

 

 

Firearm<- read.csv( “https://krkozak.github.io/MAT160/rate.csv”)head(Firearm)

 

##	year		rate
##	1	1983	4.31
##	2	1984	4.42
##	3	1985	4.52
##	4	1986	4.35
##	5	1987	4.39
##	6	1988	4.21

Code book for Data Frame Firearm

Description The data give the number of deaths caused by firearms in Australia from 1983 to 1997, expressed as a rate per 100,000 of population.

Format

This data frame contains the following columns:

Year: Years from 1983 to 1997

Rate: Rate of deaths caused by firearms in Australia per 100,000 population

Source Deaths from firearms. (2013, September 26). Retrieved from http:

//www.statsci.org/data/oz/firearms.html

References Australian Institute of Criminology, 1999.The data was con- tributed by Rex Boggs, Glenmore State High School, Rockhampton, Queens- land, Australia.

• The economic crisis of 2008 affected many countries, though some more than others. Some people in Australia have claimed that Australia wasn’t hurt that badly from the crisis. The bank assets (in billions of Australia dollars (AUD)) of the Reserve Bank of Australia (RBA) for the time period of September 1 1969 through March 1 2019 are contained in table #2.3.8 (Reserve Bank of Australia, 2019). Create a time-series plot of the assets of the RBA and interpret any findings.

## 1 Sep-6902.7NA## 2 Dec-69902.9NA## 3 Mar-701803.0NA## 4 Jun-702703.0NA
Table #2.3.8: Data of Date versus RBA Assets

Australian<- read.csv( “https://krkozak.github.io/MAT160/Australian_financial.csv”)head(Australian)

##Date Day Assets_RBA Assets_ADIs_Banks

 

 

##	5	Sep-70 360	3.0		NA
##	6	Dec-70 450	3.0		NA
##Assets_ADIs_Building Assets_ADIs_CU Assets_ADIs_Total
##	1	NA			NA	NA
##	2	NA			NA	NA
##	3	NA			NA	NA
##	4	NA			NA	NA
##	5	NA			NA	NA
##	6	NA			NA	NA
##Assets_RFCs_MM Assets_RFCs_Finance Assets_RFCs_Total
##	1	NA		NA		NA
##	2	NA		NA		NA
##	3	NA		NA		NA
##	4	NA		NA		NA
##	5	NA		NA		NA
##	6	NA		NA		NA
##Assets_Life.offices Assets_Life_funds Assets_Life_Total
##	1	NA			NA	NA
##	2	NA			NA	NA
##	3	NA			NA	NA
##	4	NA			NA	NA
##	5	NA			NA	NA
##	6	NA			NA	NA
##		Assets_Other_Public_trusts Assets_Other_Cash_trusts
##	1	NANA
##	2	NANA
##	3	NANA
##	4	NANA
##	5	NANA
##	6	NANA
##		Assets_Other_Common_funds Assets_Others_Friendly
##	1	NANA
##	2	NANA
##	3	NANA
##	4	NANA
##	5	NANA
##	6	NANA
##		Assets_Other_General_insurance Assets_Other_vehicles
##	1	NANA
##	2	NANA
##	3	NANA
##	4	NANA
##	5	NANA
##	6	NANA
##		Assets_Unconsolidated
##	1	NA

 

 

## 2NA

## 3NA

## 4NA

## 5NA

## 6NA

Code book for Data Frame Australian See Example #2.3.2

• The consumer price index (CPI) is a measure used by the U.S. government to describe the cost of living. Table #2.3.9 gives the cost of living for the

U.S. from the years 1913 through 2019, with the year 1982 being used as the year that all others are compared (Consumer Price Index Data from 1913 to 2019, 2019). Create a time-series plot of the Average Annual CPI and interpret.

Table #2.3.9: Data of Time versus CPI

CPI<- read.csv( “https://krkozak.github.io/MAT160/CPI_US.csv”)head(CPI)

 

##	Year		Jan	Feb	Mar	Apr	May	June	July	Aug	Sep	Oct
##	1	1913	9.8	9.8	9.8	9.8	9.7	9.8	9.9	9.9	10.0	10.0
##	2	1914	10.0	9.9	9.9	9.8	9.9	9.9	10.0	10.2	10.2	10.1
##	3	1915	10.1	10.0	9.9	10.0	10.1	10.1	10.1	10.1	10.1	10.2
##	4	1916	10.4	10.4	10.5	10.6	10.7	10.8	10.8	10.9	11.1	11.3
##	5	1917	11.7	12.0	12.0	12.6	12.8	13.0	12.8	13.0	13.3	13.5
##	6	1918	14.0	14.1	14.0	14.2	14.5	14.7	15.1	15.4	15.7	16.0
##Nov Dec Annual_avg PerDec_Dec Perc_Avg_Avg
##	1	10.1	10.0	9.9		–			–
##	2	10.2	10.1	10.0		1			1
##	3	10.3	10.3	10.1		2			1
##	4	11.5	11.6	10.9		12.6			7.9
##	5	13.5	13.7	12.8		18.1			17.4
##	6	16.3	16.5	15.1		20.4			18
Code book for Data frame CPI

Description This table of Consumer Price Index (CPI) data is based upon a 1982 base of 100.

Format

This data frame contains the following columns:

Year: Year from 1913 to 2019

Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec: CPI for a partic- ular month

Average_Avg: The average CPI for a particular year

 

 

PerDec_Dec: Percent change from December to December Per_Avg_Avg: Percent change from Annual Average to Annual Average

Source Consumer Price Index Data from 1913 to 2019. (2019, June 12). Re-

trieved July 10, 2019, from https://www.usinflationcalculator.com/inflation/ consumer-price-index-and-annual-percent-changes-from-1913-to-2008/

References US Inflation Calculator website, 2019.

• The mean and median incomes income in current dollars is given in Table #2.3.10. Create a time-series plot and interpret.

Table #2.3.10: Data of US Mean and Median Income

US_income<- read.csv( “https://krkozak.github.io/MAT160/US_income.csv”)head(US_income)

##year number med_income_current med_income_2017

## 1 2017 127586		61372	61372
## 2 2016 126224		59039	60309
## 3 2015 125819		56516	58476
## 4 2014 124587		53657	55613
## 5 2013 122952		51939	54744
## 6 2012 122459		51017	54569
##	mean_income_current mean_income_2017
## 1	86220	86220
## 2	83143	84931
## 3	79263	82012
## 4	75738	78500
## 5	72641	76565
## 6	71274	76237
Code book for Data Frame US_income

Description This table is of US mean and median incomes in both current dollars and in 2017 dollars.

Format

This data frame contains the following columns:

Year: Year from 1975 to 2017

number: Households as of March of the following year. (in thousands) med_income_current: median income of a US household in current dollars

med_income_2017: median income of a US household in 2017 CPI-U-RS ad- justed dollars

mean_income_current: mean income of a US household in current dollars

 

 

mean_income_2017: mean income of a US household in 2017 CPI-U-RS ad- justed dollars

Source US Census Bureau. (2018, March 06). Data. Retrieved July 21, 2019, from https://www.census.gov/programs-surveys/cps/data-detail.html

References U.S. Census Bureau, Current Population Survey, Annual Social and Economic Supplements.

 

Data Sources:

Capital and rental values of Auckland properties. (2013, September 26). Re- trieved from http://www.statsci.org/data/oz/rentcap.html

Consumer Price Index Data from 1913 to 2019. (2019, June 12). Retrieved

July 10, 2019, from https://www.usinflationcalculator.com/inflation/consumer- price-index-and-annual-percent-changes-from-1913-to-2008/

CPS News Releases. (n.d.). Retrieved July 8, 2019, from https://www.bls.gov/ cps/

Current health expenditure (% of GDP). (n.d.). Retrieved July 9, 2019, from https://data.worldbank.org/indicator/SH.XPD.CHEX.GD.ZS

Deaths from firearms. (2013, September 26). Retrieved from http://www. statsci.org/data/oz/firearms.html

Fertility rate, total (births per woman). (n.d.). Retrieved July 8, 2019, from https://data.worldbank.org/indicator/SP.DYN.TFRT.IN

Health Insurance Market Place Retrieved from website: http://aspe.hhs.gov/ health/reports/2013/marketplacepremiums/ib_premiumslandscape.pdf

John Matic provided the data from a company he worked with. The company’s name is fictitious, but the data is from an actual company.

Kozak K (2019). Survey results form surveys collected in statistics class at Coconino Community College.

Life expectancy at birth. (2013, October 14). Retrieved from http://data. worldbank.org/indicator/SP.DYN.LE00.IN

Population density (people per sq. km of land area). (n.d.). Retrieved July 9, 2019, from https://data.worldbank.org/indicator/EN.POP.DNST

Prediction of Height from Metacarpal Bone Length. (n.d.). Retrieved July 9, 2019, from http://www.statsci.org/data/general/stature.html

Pregnant women receiving prenatal care (%). (n.d.). Retrieved July 9, 2019, from https://data.worldbank.org/indicator/SH.STA.ANVC.ZS

Reserve Bank of Australia. (2019, May 13). Statistical Tables. Retrieved July 10, 2019, from https://www.rba.gov.au/statistics/tables/

 

 

Tuition and Fees, 1998-99 Through 2018-19. (2018, December 31). Retrieved from https://www.chronicle.com/interactives/tuition-and-fees

U.S. Census Bureau, Current Population Survey, Annual Social and Economic Supplements.

 

 

 

 

 

 

 

Chapter 3