8.3 Similar Triangles
Applications
When we work with similar triangles, we are harnessing the familiar power of proportions! Similar shapes are scaled versions of one another - so they are proportional.
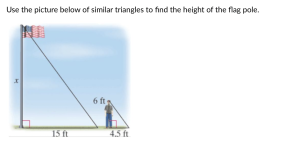
[latex]\frac{15'}{4.5'}=\frac{X}{6'}[/latex]
The parallel lines include two similar triangles, although they may be hard to see.
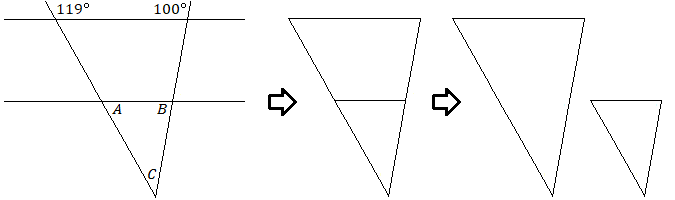
Two triangles are similar if the three angles of one triangle have the same measure as the three angles of the second triangle. The lengths of the sides of similar triangles will be in the same proportion. The triangles will have the same shape but the lengths will be scaled up or down.
We use similar triangles to find an unknown dimension on one triangle by setting up a proportion. The known side on one triangle divided by the similar known side on the other triangle make one side of the proportion. That is set equal to the unknown side divided by the similar known side.
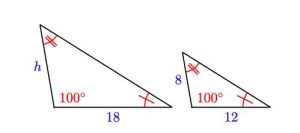 To find h in the diagram above, use the following proportion: [latex]\frac{18}{12} = \frac{h}{8}[/latex]
To find h in the diagram above, use the following proportion: [latex]\frac{18}{12} = \frac{h}{8}[/latex]
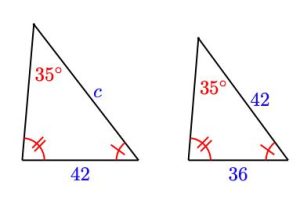 To find c in the diagram above, use the following proportion: [latex]\frac{42}{36} = \frac{c}{42}[/latex]
To find c in the diagram above, use the following proportion: [latex]\frac{42}{36} = \frac{c}{42}[/latex]
Examples: Finding Sides on Similar Triangles
Assume that each pair of triangles are similar. Use a proportion to find each unknown length.
A) 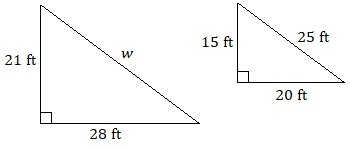
B) 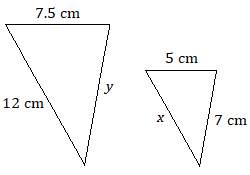
Assume that each pair of triangles are similar. Use a proportion to find each unknown length.
C) 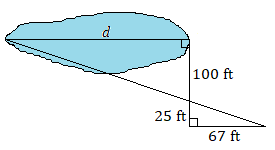
D) 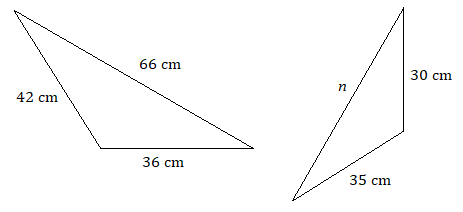
On the job, we may find similar triangles useful when dealing with a measurement that is difficult to take. We can use shadows, reflections, and angles sighted with a compass or surveying instruments to build similar triangles and solve for a measurement we are otherwise unable to take.
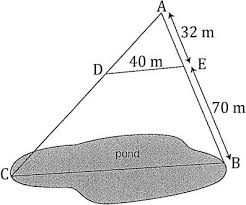
For example, you might need to get the distance across a body of water without crossing it, and can do so as follows:
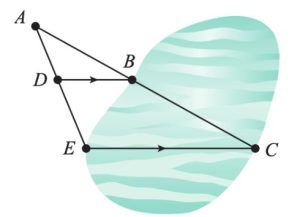
Start at Point A and sight your compass to Point C (a prominent object across the lake). Follow that heading and measure the distance you walk along that bearing to the lake shore at Point B. Turn away from the lake and walk to Point D. Record the bearing from Point D to Point B. Turn to walk toward the lake until you can face Point C at the same bearing you took from Point D to Point B. Lines DB and EC will be parallel and you've created similar triangles with a known distance from D to B. You've got enough known measurements figure out the width of the lake along either line!
Find BC [latex]\frac{AB}{AB+BC}=\frac{AD}{AE}[/latex]
or
Find EC [latex]\frac{EC}{DB}=\frac{AE}{AD}[/latex]
Examples: Applied Similar Triangles
A) Triangle A and Triangle B are similar. Triangle A has sides 2", 5" and 10". Triangle B has measurements 10", 25" and _____".
Problem Set 8.3
Each pair of triangles is similar. Use a proportion to find each unknown side or angle (x).
-
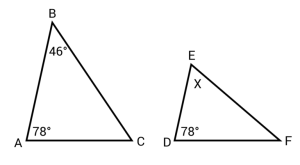
-
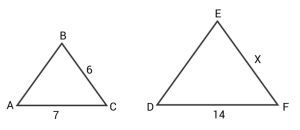
-
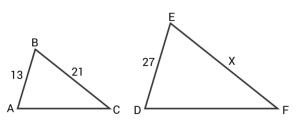
- Triangle A and Triangle B are similar. Triangle A has sides 3", 12" and 10". Triangle B has measurements 10", 40" and _____".
- You are 6' tall. You are standing with the sun at your back and your shadow measures 3'. You notice the utility pole next to you has a shadow that's 15 feet in length. How tall is that pole?
- Use the diagram here, and the lengths given to find line segment BC.
Figures that are proportional to one another. Similar triangles have the same angle measurements, but the sides are scaled up or down.