6.1 Evaluating Formulas
Morgan Chase and Marilyn Nielson
Applications
The most straightforward way to use a formula is to “evaluate an expression”. This means we plug in values for each of the variables in the formula.
The formula for basal area is as follows:
[latex]Basal Area (BA) = 0.005454 x DBH^2[/latex]
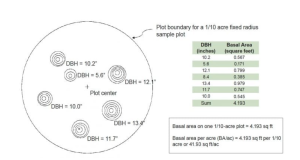
If DBH is 17 inches, what is the basal area of this tree?
A formula is an equation or set of calculations that takes a number (or numbers) as input, and produces an output. The output is often a number, but it could also be a decision such as yes or no.
Each unknown number in a formula is called a variable because its value can vary. A variable is usually represented with a letter of the alphabet. To evaluate a formula, we substitute a number (or numbers) into the formula and then perform the steps using the order of operations.
Many formulas will have just one input variable. Note: When a number is written directly next to a variable, it indicates multiplication. For example, [latex]0.24w[/latex] means [latex]0.24\cdot{w}[/latex].
Practice Exercises
The formula [latex]C=0.24w+1.26[/latex] gives the cost, in dollars, of mailing a large envelope weighing [latex]w[/latex] ounces through the USPS.[1]
- Find the cost of mailing a [latex]6[/latex]-ounce envelope.
- Find the cost of mailing a [latex]12[/latex]-ounce envelope.
Radio Cab charges the following rates for a taxi ride: a fixed fee of [latex]\textdollar3.80[/latex] to get in the taxi, plus a rate of [latex]\textdollar2.80[/latex] per mile.[2] The total cost, in dollars, of a ride [latex]m[/latex] miles long can be represented by the formula [latex]C=3.80+2.80m[/latex].
- Find the cost of a [latex]5[/latex]-mile ride.
- Find the cost of a [latex]7.5[/latex]-mile ride.
- Find the cost of getting in the taxi, then changing your mind and getting out without riding anywhere.
The number of members a state has in the U.S. House of Representatives can be approximated by the formula [latex]R=P\div{0.76}[/latex], where [latex]P[/latex] is the population in millions.[3] The 2020 populations of three states are as follows:[4]
| Oregon | [latex]4.2\text{ million}[/latex] |
| Washington | [latex]7.7\text{ million}[/latex] |
| California | [latex]39.6\text{ million}[/latex] |
Round all answers to the nearest whole number.
- How many U.S. Representatives does Oregon have?
- How many U.S. Representatives does Washington have?
- How many U.S. Representatives does California have?
The number of electoral votes a state has can be approximated by the formula [latex]E=P\div{0.76}+2[/latex], where [latex]P[/latex] is the population in millions.
- How many electoral votes does Oregon have?
- How many electoral votes does Washington have?
- How many electoral votes does California have?
Some formulas have more than one input variable. Just pay attention to which number goes in for each variable.
Practice Exercises
When a patient’s blood pressure is checked, they are usually told two numbers: the systolic blood pressure (SBP) and the diastolic blood pressure (DBP). The mean arterial pressure (MAP) can be estimated by the following formula: [latex]MAP=\frac{SBP+2\cdot{DBP}}{3}[/latex]. (The units are mm Hg.) Calculate the mean arterial pressure for each patient.
- SBP = [latex]120[/latex], DBP = [latex]75[/latex]
- SBP = [latex]140[/latex], DBP = [latex]90[/latex]
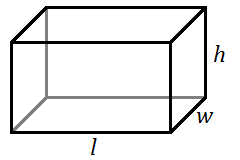UPS uses the following formula[5] to determine the “measurement” of a package with length [latex]l[/latex], width [latex]w[/latex], and height [latex]h[/latex]: [latex]m=l+2w+2h[/latex]. Determine the measurement of a package with the following dimensions.
- length [latex]18[/latex] inches, width [latex]12[/latex] inches, height [latex]14[/latex] inches
- length [latex]16[/latex] inches, width [latex]14[/latex] inches, height [latex]15[/latex] inches
Natural Resources & Water Science Formula Examples
[latex]dib = dbh-2(abt)[/latex]
Where dib = diameter inside bark; dbh = diameter at breast height; abt = average bark thickness
A) Evaluate the formula above when dbh = 22″ and abt = 1.5″
B) Evaluate the formula above when dbh = 17″ and abt = 0.75″
[latex]\%b = \frac{2(abt)}{dbh}\cdot 100[/latex]
Where %b = percent bark; abt = average bark thickness; dbh = diameter breast height
A) Evaluate the formula above when abt = 1.2″ and dbh = 24″
B) Evaluate the formula above when abt = 3″ and dbh = 41″
[latex]Q=VA[/latex]
Where Q = discharge (usually in cubic feet per second); V = velocity (usually in feet per second); A = channel area (usually in square feet)
A) Evaluate the formula above when V = 12 feet per second and A = 18 square feet
B) Evaluate the formula above when V = 26 feet per second and A = 75 square feet
C) Evaluate the formula above when V = 350 inches per hour and A = 800 square inches
[latex]RA = \frac{A}{P}[/latex]
RA = representative area; A = area; P = number of plots
A) Evaluate the formula above when A = 5 acres and P = 12 plots
B) Evaluate the formula above when A = 3 square miles and P = 100. Put your answer in acres per plot.
[latex]L=8.34QC[/latex]
L = loading (in pounds per day); Q = discharge (in million gallons per day); C = concentration (in mg per liter)
A) Evaluate the formula above when Q = 3 million gallons per day and C = 0.5 mg/liter
B) Evaluate the formula above when Q = 1.2 million gallons per day and C = 1 mg/liter
C) Evaluate the formula above when Q = 275 gallons per minute and C = 0.01 g/gallon
Problem Set 6.1
[latex]dib = dbh-2(abt)[/latex]
Where dib = diameter inside bark; dbh = diameter at breast height; abt = average bark thickness
1. Find dib when dbh = 16″ and abt = 2″
2. Find dib when dbh = 37″ and abt = 1.5″
3. Find dib when dbh = 40″ and abt = 3.2″
[latex]Q=VA[/latex]
Where Q = discharge (usually in cubic feet per second); V = velocity (usually in feet per second); A = channel area (usually in square feet)
4. Find Q when V = 30 ft/sec and A = 15 square feet
5. Find Q when V = 10 ft/sec and A = 2 square feet
6. Find Q when V = 3 ft/sec and A = 800 square inches
[latex]L=8.34QC[/latex]
L = loading (in pounds per day); Q = discharge (in million gallons per day); C = concentration (in mg per liter)
7. Find L when Q = 1.2 million gallons/day and C = 14 mg/L
8. Find L when Q = 800,000 gallons per day and C = 6 mg/L
- Source: https://pe.usps.com/text/dmm300/Notice123.htm#_c037 ↵
- Source: https://www.radiocab.net/services-radio-cab/ ↵
- The value 0.76 comes from dividing the total U.S. population in 2020, around 331 million people, by the 435 seats in the House of Representatives. ↵
- Source: https://www.census.gov/data/tables/2020/dec/2020-apportionment-data.html ↵
- Source: https://www.ups.com/us/en/help-center/packaging-and-supplies/prepare-overize.page ↵
The area (in square feet) of a tree stem at 4.5 feet above ground. We can calculate the basal area for each tree - but generally we want to know the area of each acre of land that is occupied by tree stems. This gives us a good handle on the stand density, potential value of the timber, and whether thinning treatments might be beneficial.
https://www.laforestry.com/single-post/ba-what-in-the-world-is-that-basal-area
Applications
What do technicians in our fields do? Well - much of the time we are sampling from a larger population to make inferences about that population. We might be sampling from a population of Ponderosa pine (Pinus ponderosa), a population of Bull Trout (Salvelinus confluentus), or a population of streams within a watershed.
Understanding the relationship between a population and samples we take from it (and the mathematical symbols we use when working with samples) will help you navigate this short section on statistics.
Objectives
WHen you
