7.2 Area
Morgan Chase and Marilyn Nielson
Applications
In water science, we find the area of watersheds, reservoirs, and lakes. This information is vital for water management, irrigation planning, and assessing potential flood risks. These calculations are generally completed in geographic information system (GIS) software. So you’ll jump into that soon in Introduction to GIS!
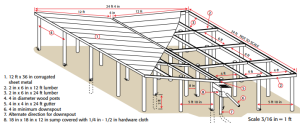
The calculations we complete by hand or in a spreadsheet will more often involve a building project. A guzzler is an inexpensive way to increase water in arid habitats and potentially support more game species. The amount of water a guzzler provides will depend on the area of its roof. The roof of a guzzler funnels rainwater and snowmelt into a water trough for wildlife.
If one inch of rain falls on the guzzler shown below, how much water (gallons) will fall into the trough?
We have seen that the perimeter of a polygon is the distance around the outside. Perimeter is a length, which is one-dimensional, and so it is measured in linear units (feet, centimeters, miles, etc.). The area of a polygon is the amount of two-dimensional space inside the polygon, and it is measured in square units: square feet, square centimeters, square miles, etc.
You can always think of area as the number of squares required to completely fill in the shape.
Area: Rectangles and Squares
Practice Exercises
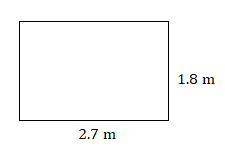
- Find the area of this rectangle.
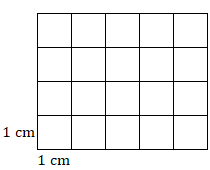
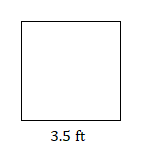
- Find the area of this square.
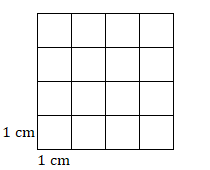
There are of course formulas for finding the areas of rectangles and squares; we don’t have to count little squares.
Area of a Rectangle
[latex]A=lw[/latex][1] or [latex]A=bh[/latex]
Area of a Square
[latex]A=s^2[/latex]
Practice Exercises
Find the area of each figure.
Examples
A) Find the area in square feet of a rectangle with sides 12 feet and 8 feet.
B) Find the area in square feet of a rug with each side 26 inches.
C) A storage shed is squeezed into the yard in a way that doesn’t allow you to measure its width. The shed is advertised as a 150 square foot shed – and you measure the length at 8 feet. What is this shed’s width in feet?
Area: Parallelograms
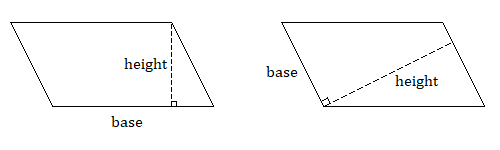
Another common polygon is the parallelogram, which looks like a tilted rectangle. As the name implies, the pairs of opposite sides are parallel and have the same length. Notice that, if we label one side as a base of the parallelogram, we have a perpendicular height which is not the length of the other sides.
The following set of diagrams shows that we can cut off part of a parallelogram and rearrange the pieces into a rectangle with the same base and height as the original parallelogram. A parallelogram with a base of [latex]7[/latex] units and a vertical height of [latex]6[/latex] units is transformed into a [latex]7[/latex] by [latex]6[/latex] rectangle, with an area of [latex]42[/latex] square units.
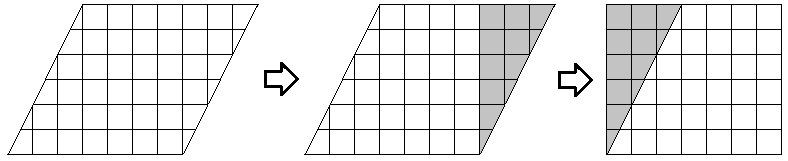
Therefore, the formula for the area of a parallelogram is identical to the formula for the area of a rectangle, provided that we are careful to use the base and the height, which must be perpendicular.
Area of a Parallelogram
[latex]A=bh[/latex]
Practice Exercises
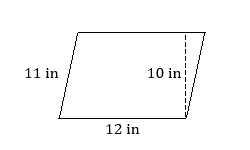
Find the area of each parallelogram.
Examples
A) A parallelogram is 10 inches high and 15 inches long. What is its area in square inches?
B) Find the height of a parallelogram with length of 15 cm and area of 375 square centimeters.
Area: Triangles
When we are finding the area of a triangle, we need to identify a base and a height that is perpendicular to that base. If the triangle is obtuse, you may have to imagine the height outside of the triangle and extend the base line to meet it.
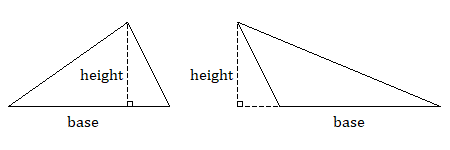
As shown below, any triangle can be doubled to form a parallelogram. Therefore, the area of a triangle is one half the area of a parallelogram with the same base and height.
Area of a Triangle
[latex]A=\frac{1}{2}bh[/latex] or [latex]A=bh\div2[/latex]
As with a parallelogram, remember that the height must be perpendicular to the base.
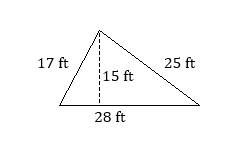
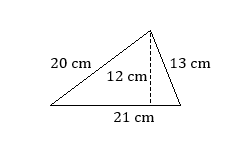
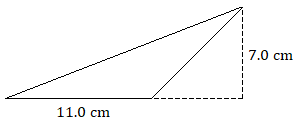
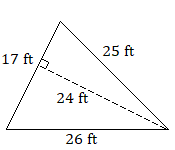
Practice Exercises
Find the area of each triangle.
Examples
A) How many square feet of fabric will you need for a triangular banner that is 3 feet tall and 1.5 feet wide at the base?
B) You aren’t quite tall enough to measure the height of a roof truss. Its base is 30 feet and its area is listed as 220 square feet. How tall is this truss?
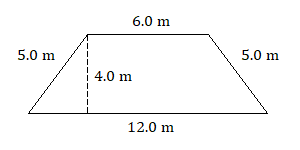
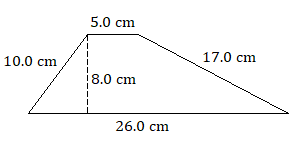
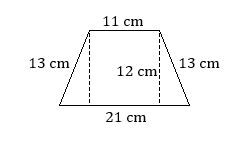
Area: Trapezoids
A somewhat less common quadrilateral is the trapezoid, which has exactly one pair of parallel sides, which we call the bases. The first example shown below is called an isosceles trapezoid because, like an isosceles triangle, its two nonparallel sides have equal lengths.
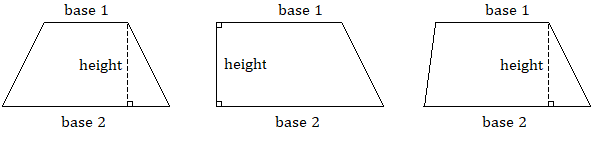
There are a number of ways to show where the area formula comes from, but the explanations are better in video because they can be animated.[2][3][4]
Area of a Trapezoid
[latex]A=\frac{1}{2}h(b_1+b_2)[/latex] or [latex]A=(b_1+b_2)h\div2[/latex]
Don’t be intimidated by the subscripts on [latex]b_1[/latex] and [latex]b_2[/latex]; it’s just a way to name two different measurements using the same letter for the variable. (Many people call the bases [latex]a[/latex] and [latex]b[/latex] instead; feel free to write it whichever way you prefer.) Whatever you call them, you just add the two bases, multiply by the height, and take half of that.
Practice Exercises
- The soaking tubs at Hot Lake Springs in La Grande, Oregon have benches formed by seven trapezoids. Each bench has an outer edge [latex]33[/latex] inches long, an inner edge [latex]23[/latex] inches long, and the edges are [latex]11[/latex] inches apart. How much seating area do the benches provide? (Ignore the gaps between the boards.)
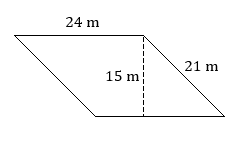
Find the area of each trapezoid.
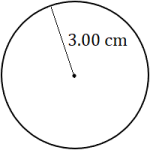
Area: Circles
The area of a circle is [latex]\pi[/latex] times the square of the radius: [latex]A=\pi{r^2}[/latex]. The units are still square units, even though a circle is round. (Think of the squares on a round waffle.) Because we can’t fit a whole number of squares—or an exact fraction of squares—inside the circle, the area of a circle will be an approximation.
If your calculator doesn’t have a [latex]\pi[/latex] key, use the approximation [latex]\pi\approx3.1416[/latex].
Area of a Circle
[latex]A=\pi{r^2}[/latex]
Practice Exercises
Find the area of each circle. Round each answer to the appropriate number of significant figures.
Examples
A) A watering tank has a diameter of 8 feet. How many square feet of wire mesh will be needed to create a cover for it?
B) A Ponderosa pine tree measures 32 inches in diameter. What is its basal area in square feet?
C) What is the radius of a one-quarter acre plot?
Problem Set 7.2
- Find the area in square meters of a rectangle with sides 4 meters and 6 meters.
- Find the area in square feet of a glass pane with each side 18 inches.
- Building codes specify that a room can be no smaller than 70 square feet. You’re reviewing building plans for cottages at your state park. The cottages are 18 feet wide and 25 feet long. If you want to use the back of the cottage for two equally-sized bedrooms (9 foot wide for each). What will the depth of each room need to be at a minimum?
- A triangular roof truss is 40 feet wide and 12 feet tall. What is its area?
- If the area of your triangle is 400 square meters, and the base is 200 feet, what is the height in feet?
- Your new, round, Japanese soaking tub will stay warm longer if you cover it. The diameter of the tub is 3 meters. How many square feet of insulating fabric will you need to cover the tub?
- A cedar tree measures 102 inches in circumference. If you were to cut this tree down and measure the area of the top of the stump (basal area), what would it be?
- A Ponderosa pine tree measures 40 inches in diameter. What is the basal area of this tree?
- How many acres does a circular plot with a radius of 50 feet encompass?
- What is the radius of a circular plot with an area of 1/10-acre?
- You might choose to use capital letters for the variables here because a lowercase letter "l" can easily be mistaken for a number "1". ↵
- https://youtu.be/yTnYRpcZA9c ↵
- https://youtu.be/WZtO3oERges ↵
- https://youtu.be/uLHc6Br2veg ↵
a man-made water collection system that collects rainwater and snowmelt, and stores it to provide drinking water for wildlife.
