7.3 Volume
Morgan Chase and Marilyn Nielson
Applications
A fun application is calculating the volume in a pile of woodchips. Engineered wood manufacturers and pulp mills carefully track their available inputs in order to efficiently produce paper, oriented strand board, medium-density fiberboard, and other products. In fact, mills fly drones over their yards to take measurements of the input piles and calculate available volume.
If you have a pile with a diameter of 15 feet and a height of 20 feet, about how many cubic yards of chips are present?
The surface area of a solid is the sum of the areas of all its faces; therefore, surface area is two-dimensional and measured in square units. The volume is the amount of space inside the solid. Volume is three-dimensional, measured in cubic units. You can imagine the volume as the number of cubes required to completely fill up the solid.
Volume: Rectangular Solids
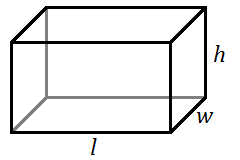
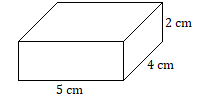
Volume of a Rectangular Solid
For a rectangular solid with length [latex]l[/latex], width [latex]w[/latex], and height [latex]h[/latex]:
[latex]V=lwh[/latex]
For a cube with side length [latex]s[/latex]:
[latex]V=s^3[/latex]
Examples
A) How many gallons will fill a tank 40″ x 24″ x 18″?
B) A cord of wood is a stack 4 feet tall, 8 feet long, and 4 feet wide. How many cubic feet are in a cord? How many cubic yards are in a cord?
C) A road is 12 feet wide and will be graveled for 2 miles. The gravel needs to be 5 inches deep. How many cubic yards of gravel should you order?
View answers.
Watch solutions video.
Practice Exercises
Find the volume of each solid.
Volume: Rectangular Prisms
A solid with two equal sized polygons as its bases and rectangular lateral faces is called a right-angle prism. Some examples are shown below. We will refer to them simply as prisms in this textbook. (We will not be working with oblique prisms, which have parallelograms for the lateral faces.)
If you know the area of one of the bases, multiplying it by the height gives you the volume of the prism. In the formula below, we are using a capital [latex]B[/latex] to represent the area of the base.
Volume of a Prism
For a prism with base area [latex]B[/latex] and height [latex]h[/latex]:
[latex]V=Bh[/latex]
If the prism is lying on its side, the “height” will look like a length. No matter how the prism is oriented, the height is the dimension that is perpendicular to the planes of the two parallel bases.
Examples
A) What volume of acrylic (cubic inches) will be needed to create a prism with triangular bases 0.75 inches wide and 1 inch tall – and an overall height of 2 inches?
View answers.
Watch solutions video.
Practice Exercises
Find the volume of each prism.
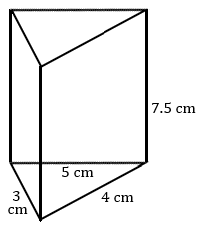
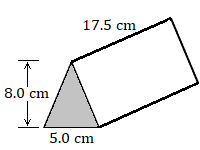
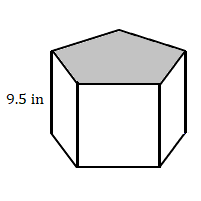
The area of the pentagon is 55 square inches.
Volume: Cylinders
A cylinder can be thought of as a prism with bases that are circles, rather than polygons. Just as with a prism, the volume is the area of the base multiplied by the height.
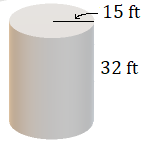
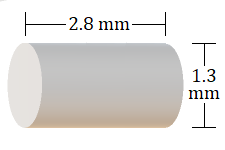
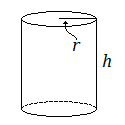Volume of a Cylinder
For a cylinder with radius [latex]r[/latex] (or diameter [latex]d[/latex]) and height [latex]h[/latex]:
[latex]V=\pi{r^2}h[/latex] or [latex]V=\pi{d^2}h\div4[/latex]
Examples
A) A bucket has a radius of 8 inches and a height of 24 inches. How many cubic inches of water can it hold? How many cubic feet? Gallons?
B) How many gallons will a 12 inch wide culvert that is 10 feet long hold?
View answers.
Watch solutions video.
Practice Exercises
Find the volume of each cylinder.
Volume: Spheres & Cones
As with surface area, we would need to use calculus to derive the formula for the volume of a sphere. Just believe it. 
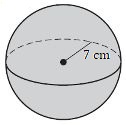
Volume of a Sphere
For a sphere with radius [latex]r[/latex] or diameter [latex]d[/latex]:
[latex]V=4\pi{r^3}\div3[/latex] or [latex]V=\pi{d^3}\div6[/latex]
Volume of a Cone
[latex]V=\frac{1}{3}\Pi\cdot r^2\cdot h[/latex]
Examples
A) The solid waster digesters at our water treatment facility are spheres with a radius of 20 feet. How many cubic feet of waste could they hold if full? How many gallons is this?
B) If you have a wood chip pile with a diameter of 15 feet and a height of 20 feet, about how many cubic yards of chips are present?
View answers.
Watch solutions video.
Practice Exercises
Find the volume of each sphere.
Volume: Composite Solids
Of course, not every three-dimensional object is a prism, cylinder, or sphere. A composite solid is made up of two or more simpler solids. As with two-dimensional composite figures, breaking the figure into recognizable solids is a good first step.
Examples
A) Let’s figure out the volume of grain we could store in a cylindrical silo with a cone roof (if we could fill it entirely). The cylinder is 12 feet wide at the base and 20 feet tall. The cone roof is 5 feet tall at its peak.
View answers.
Watch solutions video.
Practice Exercises
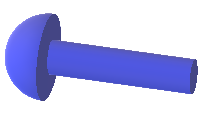
- A rivet is formed by topping a cylinder with a hemisphere. The width of the cylindrical part (the rivet pin) is [latex]1.6[/latex] cm and the length is [latex]7.0[/latex] cm. The width of the hemisphere-shaped top (the rivet head) is [latex]3.2[/latex] cm. Find the rivet’s volume.
A [latex]250[/latex]-gallon propane tank is roughly in the shape of a cylinder with a hemisphere on each end. The length of the cylindrical part is [latex]6.0[/latex] feet long, and the cross-sectional diameter of the tank is [latex]2.5[/latex] feet.
- Calculate the volume of the tank in cubic feet.
- Verify that the tank can hold [latex]250[/latex] gallons of liquid propane.
Problem Set 7.3
- How many gallons will fill a rectangular fish tank 18″ x 24″ x 48″?
- The Winchester bushel is the volume of a cylinder 18.5 in (470 mm) in diameter and 8 in (200 mm) high. How many gallons are in a Winchester bushel? How many cubic centimeters (cc) are in a Winchester bushel?
- A railroad car is 62 feet by 10.5 feet. How many cubic yards can it hold?
- You need to spread landscape bark within a playgound area that measures 30 meters by 50 meters. Bark needs to have a depth of 20 cm. How many cubic meters of landscape bark will you need?
- A log measures 32 inches diameter and 42 feet long. What is the volume of this log in cubic inches? What is the volume in cubic feet?
- A “5-gallon” bucket has a diameter of 254 mm and a height of 368 mm. What is the maximum volume it can hold in gallons?
- How many cubic feet of water can a 16″ diameter culvert hold if it is 20 feet long?
- The chip pile at a wood products facility measures 25 feet diameter at its base. If the pile is 17 feet tall, how many cubic yards does it contain?
- What volume of insulation will you need to completely fill your attic? In your house, the attic is formed by triangular trusses 12 feet tall with a base of 24 feet. The house is 32 feet wide.
- A valve wasn’t closed properly at a fill station. All night oil leaked onto the ground surface. Luckily, a clay hardpan layer in the soil kept this oil from reaching more than 3 feet deep, but it has spread out evenly to form a circular spill area with a radius of 20 feet. We need to excavate down to the hardpan to include all material within this spill zone. How many cubic yards of material do we need to excavate for this cleanup project?
