Applications

What does 112° 47′ 22″ mean? Could you draw something to represent this measurement? What tool would you need?

We can visualize an angle as the figure formed when two line segments share a common endpoint. We can also think about an angle as a measure of rotation. One full rotation or a full circle is [latex]360^\circ[/latex], so a half rotation or U-turn is [latex]180^\circ[/latex], and a quarter turn is [latex]90^\circ[/latex]. We often classify angles by their size relative to these [latex]90^\circ[/latex] and [latex]180^\circ[/latex] benchmarks.

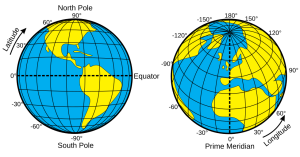
How are latitude and longitude angles?

Conveniently, we can locate any spot on the surface of the earth if we split the globe in half along the equator and measure the angle from the center of the earth to a point on its surface to get latitude – and then split the earth along the prime meridian and measure the angle east or west to get longitude.

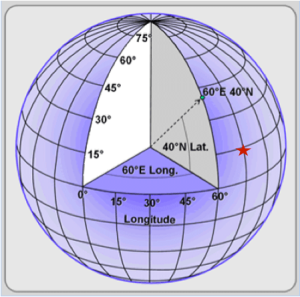
A precise way to measure angles is with degrees, minutes, and seconds. A degree is the angle formed by  [latex]\frac{1}{360}th[/latex] of a full circle. A minute is [latex]\frac{1}{60}th[/latex] of a degree. A second is [latex]\frac{1}{60}th[/latex] of a minute. So, there are 3,600 seconds in each degree. Reporting an angle to the seconds has a lot of precision!

When we report latitude and longitude using degrees, minutes, seconds we include the direction so that folks know whether we are north or south of the equator or east or west of the prime meridian. Spokane, Washington is located at 47° 37′ 48″ N and 117° 31′ 47″ W.

Why all the bases of 60? The Babylonians first explored this arena and their numbering system hinged on bases of 60 (rather than bases of 10 like ours does today).

Software sometimes requires we enter angles as decimal degrees rather than degrees, minutes and seconds. When this is needed, we convert from degrees, minutes, seconds to decimal degrees as follows:

1. Divide the minutes by 60
2. Divide the seconds by 3,600
3. Add these together and add them to the whole degrees.
4. Use positive or negative signs to indicate the Earth’s quadrant.

Here’s what it looks like with Spokane’s location:

47° 37′ 48″ N

• [latex]47+\frac{37}{60}+\frac{48}{3600}[/latex]
• North is indicated with a +
• +47.63º

117° 31′ 47″ W

• [latex]117+\frac{31}{60}+\frac{47}{3600}[/latex]
• West is indicated with a –
• -117.52972°

To go the other direction, from decimal degrees to degrees, minutes, seconds, follow these steps:

1. Pull the whole degrees off.
2. Multiply the remaining decimal by 60. The whole number is your minutes.
3. Take the remaining decimal and multiply that by 60. This is your seconds.
4. Add N or S and E or W.

Could you have a decimal in the minutes place? Why or why not? What about a decimal in the seconds place?

Here’s what the process looks like for the latitude and longitude in Spokane:

+47.63º

• 47º
• 0.63 x  60 = 37.8′  so  37′
• 0.8 x 60 = 48″
• 47° 37′ 48″ N

-117.52972°

• 117°
• 0.52972 x 60 = 31.7832′ so 31′
• 0.7832 x 60 = 46.992″ so 47″
• 117° 31′ 47″ W

We can add and subtract degrees, minutes, seconds on paper by working with bases of 60. It’s kind of fun! Here’s ow:

Line up the columns by degrees, then minutes, then seconds. Add from right to left, beginning with seconds. Then, check – are the seconds greater than 60? If so, subtract 60 from the seconds and add 1 to the minutes column. Now check the minutes. Are there more than 60 minutes? If so, subtract 60 from the minutes and add one to the degrees. Follow along in the examples to watch this in action.

When you subtract, the process will be similar to subtracting on paper, like you learned in third grade. Instead of “borrowing” 10’s though, we’ll take units of 60.

Check these examples to see the process in action.