8.2 Some Properties of Triangles
Applications

We see triangles frequently in nature. What naturally occurring triangles have you seen lately? A triangular shape allows many conifers to effectively shed snow and triangles provide excellent force distribution as seen in the design of trusses and bridges.
What Makes a Triangle?
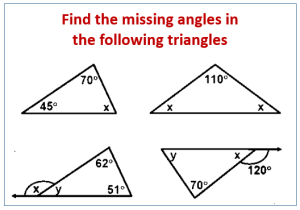
If you connect three line segments into a polygon – you’ve got a triangle! Three sides and three angles define this shape. The interior angles of all triangles add to 180°. We often use this property to find the measure of a missing angle.
(On a related tangent… Sometimes we use the term supplementary to describe two angles that add to 180 ° and the term complementary to describe two angles that add to 90 °.)
Examples: Finding the Missing Angle of a Triangle
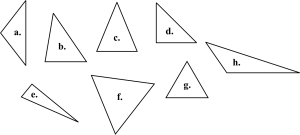
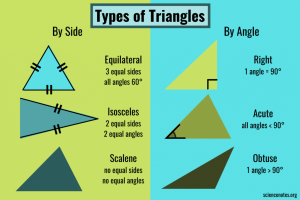
Classifying Triangles
We can classify triangles into three categories based on the lengths of their sides.
- Equilateral triangle: all three sides have the same length
- Isosceles triangle: exactly two sides have the same length
- Scalene triangle: all three sides have different lengths
We can also classify triangles into three categories based on the measures of their angles.
- Obtuse triangle: one of the angles is an obtuse angle
- Right triangle: one of the angles is a right angle
- Acute triangle: all three of the angles are acute
Examples: Describing Triangles
Relationships Among Sides and Angles
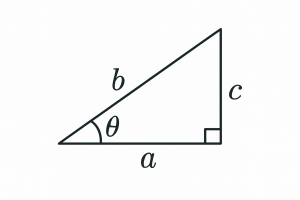
We use specific terms to refer to the sides and angles of a triangle and their relationship to one another. The side of a triangle directly across from an angle is called opposite with respect to that angle. Another way to see this is that this opposite side is not one of the lines that forms the angle. If a side is one of the lines that forms the angle, it is referred to as adjacent to that angle. In a right triangle, the side opposite of the 90 deg angle is called the hypotenuse. It is the longest side of the triangle because it is opposite the largest angle.

Examples: Find the Opposite, Adjacent and Hypotenuse
Problem Set 8.2
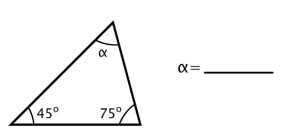
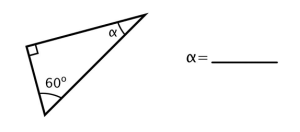
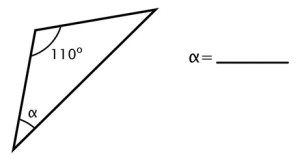
Use the terms right, acute, obtuse and equilateral, scalene, isosceles to describe these triangles. Then, find the missing angle.
1)
2)
3) 
Identify the indicated sides relative to angle Θ for the following triangle.
4) Which side is the hypotenuse?
5) Which side is opposite Θ?
6) Which side is adjacent to Θ?
Two angles than add to 180 degrees.
Two angles whose measures add to 90 degrees.
The side of a triangle that is directly across from an angle. The opposite side is not one of the lines that forms the angle.
The side of a triangle that forms part of the angle you are referring to. In a right triangle, the hypotenuse and the adjacent side form the angle.
The longest side of a right triangle. It is opposite the 90 degree angle.