8.6 Working with Slopes in Percent
Applications
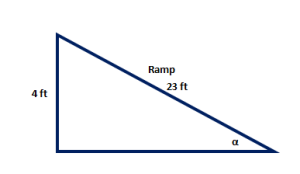
Have you ever seen a warning sign on a roadway announcing a steep section ahead?

Percents are used to describe the angle of a slope and in other applications where we use right triangles. What does the 14% on this sign mean? Can you spot the right triangle on the sign? If so, which angle in the triangle corresponds to 14%? If we were to measure that angle in degrees, what would it be?
Slope As a Percent
- A line that is increasing in height has a positive slope.
- A line that is decreasing in height has a negative slope.[2]
- The slope of a horizontal line is 0; it is not increasing or decreasing.
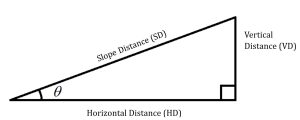
When we are working in the field on land that isn't flat the distance we walk is the slope distance. The distance we measure on a map is the horizontal distance. We can find the vertical distance by counting elevation contours on a topographic map.
Calculating Slope Angle in Percent
A slope may be expressed as a ratio, a decimal, or a percent. For example, consider this loading ramp with a vertical distance of 23.5 inches and a horizontal distance of 132 inches.
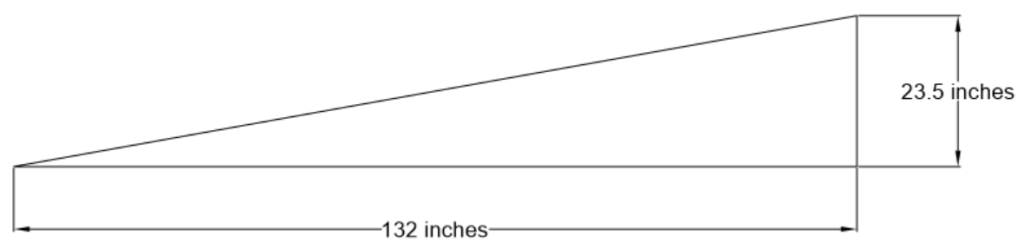
As a Ratio
We express slope as a ratio as VD:HD or [latex]\frac{VD}{HD}[/latex]
For the ramp illustrated above 23.5:132 or [latex]\frac{23.5}{132}[/latex]. We can reduce this ratio to 1:5.62.
As a Decimal
If we divide the vertical distance by the horizontal distance, we get slope as a decimal. In the above ramp [latex]\frac{23.5}{132} = 0.18[/latex].
As a Percent
Expressing slope as a percent means describing the vertical distance that is gained (or lost) when the horizontal distance is set to 100. We take slope as a decimal, and multiply it by 100 to express slope as a percent. In the above ramp...
[latex](\frac{23.5}{132} = 0.18)*100 \to 18[/latex]%.
...or 18 inches of vertical gain for every 100 inches of horizontal distance.
Examples: Finding Slope in Degrees, Decimals, or Percent
A) Find the slope as a ratio, decimal, percent and in degrees.
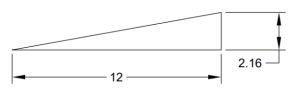
(This is the preferred maximum slope for open pit mines.)
Practice Exercises
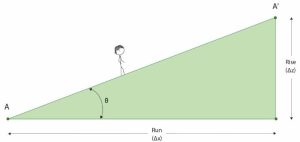
The steepness of a line may also be described by its angle of elevation above the horizontal (or its angle of depression below the horizontal).
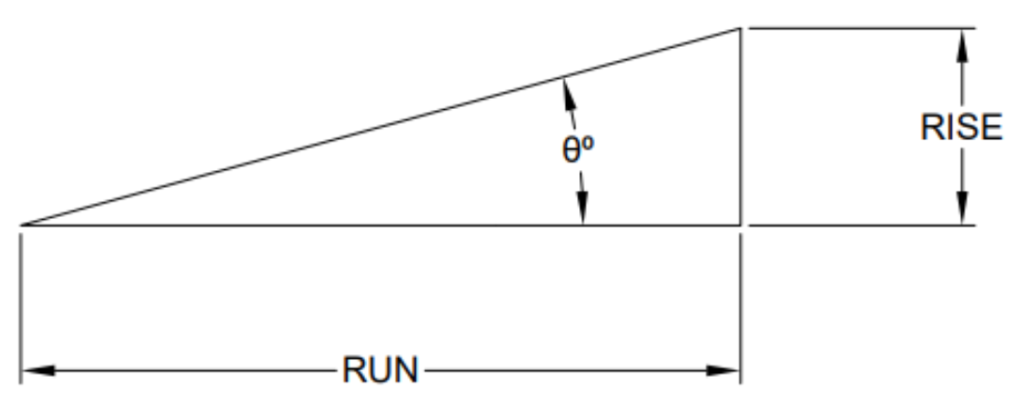
Notice that the vertical rise is the side opposite the angle, and the horizontal run is the side adjacent to the angle. Therefore, trigonometry tells us that [latex]\text{tangent}=\frac{\text{opposite}}{\text{adjacent}}=\frac{\text{rise}}{\text{run}}[/latex]. The tangent of the angle is equal to the slope.
Or, thinking about it in reverse, the inverse tangent of the slope is the angle.
[latex]\text{tan}^{-1}\left(\frac{\text{rise}}{\text{run}}\right)=\theta[/latex]
When we are looking at slope as a right triangle, the following terms will be synonymous:
Run = Horizontal Distance (HD) (also the distance if calculated from a map)
Rise = Vertical Distance (VD) (you can get this by counting contour lines on a topo map!)
Distance along the Hypotenuse = Slope Distance (SD)
Finding Vertical, Horizontal and Slope Distance
If we know the slope angle and one of the sides of the slope triangle, we can readily find the others. We can use this proportion showing the relationship between vertical distance, horizontal distance, and percent slope.
[latex]\frac{VD}{HD}=\frac{Slope Angle}{100}[/latex]
...or, we can use similar triangles. When we know the slope angle, we know what the vertical distance is when the horizontal distance is 100. For example, if my slope angle is 7%, I can make a triangle that represents the situation when the horizontal distance is 100 feet.
The Pythagorean Theorem gets us the slope distance (hypotenuse). Now, if I'm on a slope of 7% and I know one measurement, I can find the others.
For example, if I've walked the slope and measured a slope distance of 25 feet, I can find the horizontal distance as follows:
[latex]\frac{100}{100.24}=\frac{HD}{25}[/latex]
So, the horizontal distance is 24.94 feet for every 25 feet I walk on a slope of 7%.
Examples: Finding Slope
Relating Slope Angle in Percent to Slope Angle in Degrees
Let's use the triangle we drew for a 7% slope to illustrate how slope in percent is related to slope in degrees.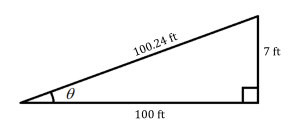
You've already got trigonometry skills, right? How would you find the angle (\Theta) above in degrees?
[latex]\Theta=\tan^{-1}(\frac{7}{100})[/latex]
To find the slope in degrees, given the slope in percent, use the following:
[latex]\Theta\:{\text{in degrees}}=\tan^{-1}(\frac{\text{slope angle in percent}}{100})[/latex]
Slope in percent is the vertical distance (opposite side) divided by the horizontal distance (adjacent side) - so it's the tangent of the slope angle in degrees!
To find the slope in percent, given the slope in degrees, use the following:
[latex]\Theta\:{\text{in percent}}=\tan(\theta\:{\text{in degrees}})*100[/latex]
You probably have an intuitive feeling for angles from 0° to 90°. As a percent, these would range from 0% to over 5,270% as the vertical distance (rise) becomes longer than the horizontal distance (run). (We actually can't take tan 90° because it is undefined. Because the tangent function is defined as sin θ/cos θ, when cos θ becomes zero, the tangent function becomes undefined.) A slope of 45° is equivalent to a 100% slope because the rise is equal to the run. Slopes over 45° will be greater than 100%.
Examples: Converting Slope Between Percent and Degrees
Examples: Applying Slope
A) SD = 124' Slope Angle = 5° Find HD and VD.
B) Slope Angle = 15° HD = 125' Find SD and VD.
C) HD = 120' VD = -12' Find SD and Slope Angle.
D) You're on a slope of 12° and measure along the ground a distance of 100 feet (SD). How far is this as a horizontal distance?
Check out Forest Measurements by Joan DeYoung. It has an excellent discussion of slope and its measurement and applications in the field of forestry.
Practice Exercises
For exercises 5 through 8, determine the angle of elevation for each slope. Round to the nearest hundredth of a degree.
For proper drainage, the ground around a building should slope downwards, away from the building.
9. The minimum downward grade of the ground is 1%. Assuming this grade, if a point on the ground is 50 feet horizontally from the base of the house, how much lower is the ground at that point?
10. The preferred minimum downward grade of the ground is 2%. Assuming this grade, if a point on the ground is 50 feet horizontally from the base of the house, how much lower is the ground at that point?
11. The maximum acceptable downward grade of the ground is 10%. Assuming this grade, if a point on the ground is 50 feet horizontally from the base of the house, how much lower is the ground at that point?
12. A motion sensor needs to be installed on the outside of a warehouse door 12 feet above the ground. The sensor should go off if anyone approaching the warehouse gets within 20 feet of the door. What angle from vertical should the sensor point away from the building to detect someone at the appropriate distance from the warehouse? Round your answer to the nearest degree.
13. A ramp is being constructed to the entrance to a public building that is 2.5 feet higher than the level courtyard in front of the entrance. Assuming that the ramp will be continuous with no switchbacks or level platforms,[3] what is the minimum horizontal distance required for the ramp so that it will comply with ADA regulations?
View Answers to Practice Exercises
Problem Set 8.6
Find the slope (Θ) as a ratio, decimal, percent and in degrees.
1) If the horizontal distance (run) is 50 feet and the vertical distance (rise) is 10 feet.
2) If the horizontal distance (run) is 20 feet and the vertical distance (rise) is 15 feet.
3) If the horizontal distance (run) is 100 meters and the vertical distance (rise) is 45 centimeters.
4) If the slope distance (hypotenuse) walked is 150 feet and the vertical distance (rise) is 30 feet.
5) Convert a slope of 17% to degrees.
6) Convert a slope of 0.2% to degrees.
7) Convert a slope of 3° to percent.
8) Convert a slope of 15° to percent.
9) A slope rises 40 feet for every horizontal mile. What is the slope angle in degrees? As a percent?
10) You're on a slope of 18° and measure along the ground a distance of 100 feet (SD). How far is this as a horizontal distance?
11) You're on a slope of 8% and measure along the ground a distance of 100 feet (SD). How far is this as a horizontal distance?
12) On a map, you place a proposed 1,000-foot fenceline. The fence runs directly up a slope of 20%. What will the actual length of the fenceline on the ground?
13) Two points on a map are 2.125 inches apart. The map scale is 1:10,000. The starting elevation is 700 feet and the ending elevation is 1,350 feet. What is the ground distance between the points? What is the slope in percent? What is the slope in degrees? What is the slope distance between the two points?
14) Two points on a map are 4 cm apart. The map scale is 1:50,000. The starting elevation is 1,200 feet and the ending elevation is 1,650 feet. What is the ground distance between the points in kilometers? What is the slope in percent? What is the slope in degrees? What is the slope distance between the two points in kilometers?
15) Your ramp can't exceed a slope of 20%. If the ramp needs to access a porch that is 3 feet above ground level, how long will the ramp need to be?
- Source: https://www.ada-compliance.com/ada-compliance/403-walking-surfaces ↵
- Source: https://www.ada-compliance.com/ada-compliance/405-ramps ↵
- If you were curious, this is the maximum rise allowed for this situation; a rise of more than 2.5 feet would require a switchback or a level platform. ↵