"

8.7 Triangles are the Answer! Solving Applied Problems

Bob Brown; Morgan Chase; and Marilyn Nielson

Applications

Objectives

When you’ve completed this chapter, you’ll be comfortable with the following:

  1. Diagramming applied problems to see where right triangles can provide a solution.
  2. Applying right-triangle geometry to solve applied problems.

Here’s an age-old forestry problem: How tall is this tree?

 

American elm in Wisconsin. A view up the trunk.
Do you need to climb it to get its height?
The Hendricks Creek survivor elm stands on lands managed by the Wisconsin Board of Commissioners of Public Lands in northern Wisconsin. USDA Forest Service photo by Linda Haugen.

What do you need to know to find the height of this tree? How could you collect that data? What tools would you need? What about measuring the height of the tree if you are standing on a slope? We’ll apply right triangles to this situation and many others!

 

Instruments for Measuring Angles

Outside of a surveying environment, we’ll generally use a clinometer or relaskop to measure  vertical angles (up and down) and a compass to measure horizontal angles (back and forth). A clinometer will have two scales – one in percent and another in degrees or topographic. We’ll use the percent or topographic scale when measuring slopes and heights because the calculations can be done in your head.

This clinometer shows a percent scale and a topographic scale (1:66).

 

The relaskop was invented during the 1940s and shared with the world in a paper published in 1948. To learn more about its invention watch this 8-minute video clip.

 

This sighting compass can accurately find bearings in the field.

Slopes

Soon enough, you’ll learn how to measure the slope angle using a clinometer or relaskop in the field!

Slopes on maps

What if you’re presented with a topographic map and asked to find the slope? The distance you measure on the map represents the horizontal distance of the slope triangle (after you have converted it from the map distance to a ground distance). If you were to walk that same path on the ground, you’d be walking the slope distance.

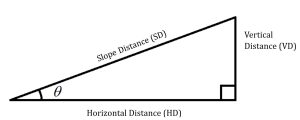A triangle showing the slope distance (hypotenuse), vertical distance (rise), and horizontal distance (run)You’ll find the slope angle of a map segment using [latex]Slope Angle in Percent = \frac{VD}{HD} * 100[/latex], where the the vertical distance (VD) is the number of contour lines crossed by that segment multiplied by the contour interval – and the horizontal distance is the ground distance along the segment.

Examples: Slope on a Topographic Map

A) Point A is at 1200′ and Point B is at 1600′. The distance between them on a 1:24000 scale map is 1.25 inches. What is the slope between these points in percent?

B) Your 1:24000 – scale map has contour lines at 40′ intervals. If you count 8 contour lines between the landing and your harvest area and the distance is 2.75 inches, what is the average slope between these areas? In percent? In degrees?

View answers.

Watch solutions video.

Slopes for Ladders and Ramps

We’ll see several situations where calculating the slope angle is needed given two of the sides of the slope triangle. In these cases, you’ll likely have a slope angle that you need to stay below or above for safety or accessibility. For example, a ladder is set up for optimal safety if its vertical distance is four times the horizontal distance it lies from the base of the object being climbed (400% slope or about 76°).

Ladder Angle: What is the '1 in 4' Rule?

To meet accessibility requirements under the Americans with Disabilities Acts (ADA), ramps need to have a slope ratio of 1:12 (8.3%) or less and are limited to a maximum horizontal distance of 30 feet.

Examples: Ladders and Ramps

A) My ladder is 50′ tall. Can I safely access a 35′ tall roof with it?

B) How long does my ramp need to be to meet ADA criteria while reaching a porch that’s 3′ high?

View answers.

Watch solutions video.

Slopes for Trails

On a trail, the distance you walk is the slope distance (SD), and it’s the hypotenuse of the slope triangle. The horizontal distance (HD) is the distance measured on a map and the vertical distance (VD) is the difference between your starting and finishing elevations.



The Forest Service has developed guidelines for ADA accessible trails that include the following parameters:


    

  • 1:20 (5 percent) for any distance
    • 

  • 1:12 (8.33 percent) for up to 200 feet (61 meters)
    • 

  • 1:10 (10 percent) for up to 30 feet (9 meters)
    • 

  • 1:8 (12.5 percent) for up to 10 feet (3 meters)
    • 

  • 1:7 (14 percent) into and out of drain dips for up to 5 feet (1.5 meters) where the cross slope does not exceed 1:10
    • 

  • Cross slopes should not exceed 1:20 (5 percent)
    • 





 


Illustration of a person with a day pack hiking uphill on a trail. Text and arrows indicate that cross slope is perpendicular to the trail, and running slope is along the trail's length.


 


Trails built with a grade less than half the side slope (slope of the hillside the trail traverses) are more resistant to erosion. In general, trails with an average slope greater than 40% are considered extremely challenging.


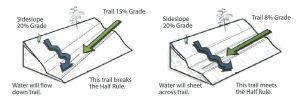Given these parameters, we can design trails over a variety of terrain!






Examples: Trails and Slope






A) You want your trail to maintain an average slope of 10% while it climbs from a base elevation of 1,200 feet to a peak at 3,400 feet. How long will the trail need to be to maintain this average slope?


B) What is the average slope of a trail that gains 800 feet over a walked distance of 2 miles?


View answers.


Watch solutions video.






Heights


Let’s leave the world of slope for a moment to examine how we can use our distance from a tall object (like a tree) and the angles to the top and the bottom of the object to find its height.


Measurements in Degrees


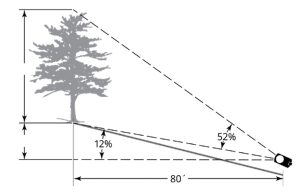
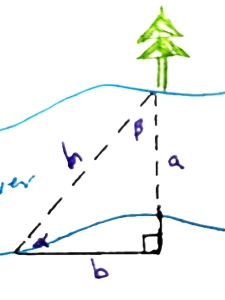
Check out the sweet triangle we can make with a tree! Which parameters can we measure easily in the field?


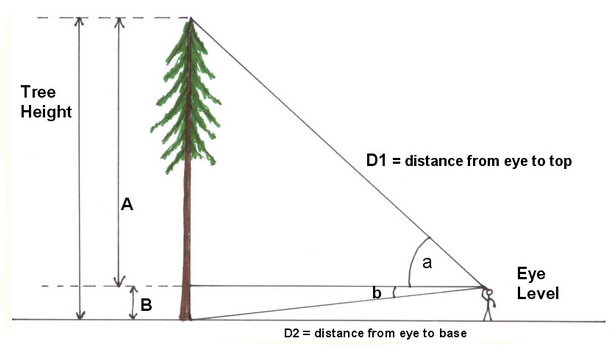
Diagram showing the elements involved measuring tree height on flat ground.


On flat ground, if you’ve got the angle to the top of an object, the angle to the bottom of an object, and you know your distance from the object – you can build a couple of straightforward triangles.


 


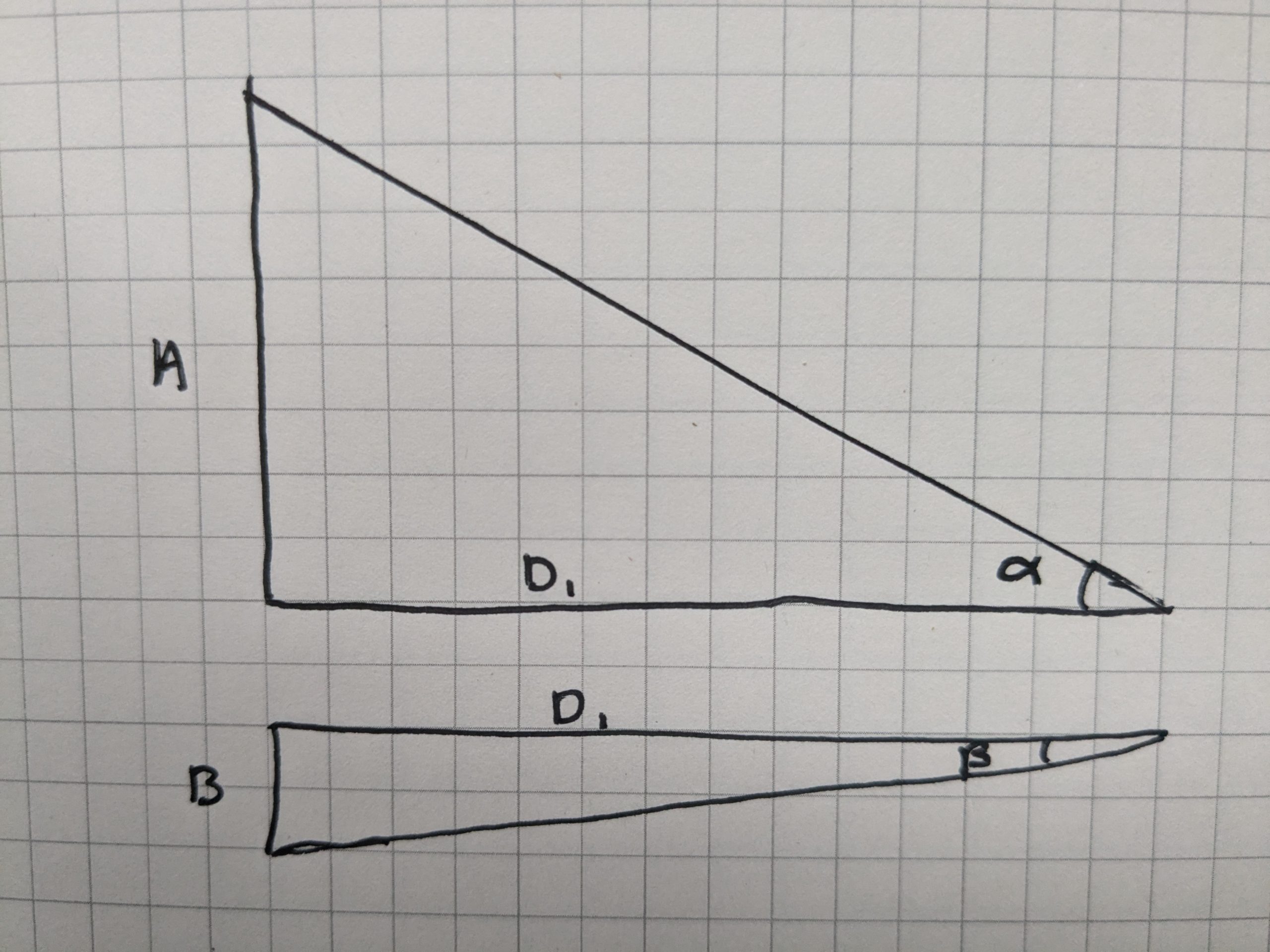
Two triangles created when measuring tree height on flat ground.


The tangent of α will be height A divided by length D1 (the horizontal distance HD). So, we can find height A by multiplying the tangent α by the distance from the tree, and we can find height B by multiplying the tangent β by the distance from the tree (HD). So, the total height of the tree (A+B) is equal to:




[latex]D\small 1 \cdot \tan\α+D\small 1 \cdot \tan\\β = Height[/latex]


Simplified


[latex]D\small 1 (\tan\α+\tan\β) = Height[/latex]




 


 


Measurements in Percent


Measurements in percent are straightforward. Stand at a convenient distance, sight the top of the object and read the % scale (%T). Sight the bottom of the object and read the % scale (%B). Subtract the bottom reading from the top reading and multiply by your horizontal distance from the object.


[latex]Height= (%T-%B)*HD[/latex]


 


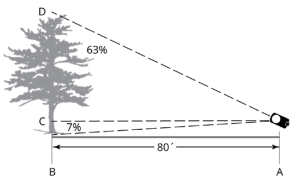
Using the percent scale to sight to the top and bottom of a tree. How tall is this one?






Examples: Heights of Objects






A) How tall is this one???




View answer.


Watch solutions video.






Heights on a Slope


When we measure trees in the field, we’ll usually be standing on a slope (at least in this part of the world!). The distance that we measure by pulling a tape or pacing chains will be a slope distance (SD). We can get the slope angle with a clinometer. We can also get the angle to the top of a tree and the angle to the bottom of  a tree with a clinometer.


Measurements in Degrees


If we are working in degrees, how can we put these measurements together to arrive at the tree’s height?






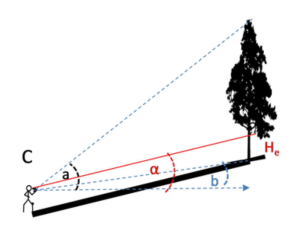
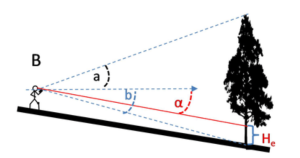
Our first step is to get our horizontal distance from the tree. We can derive this from the slope distance (that we measured by pacing or pulling a tape/chain) and the slope angle (that we measured using a clinometer or similar tool).




[latex]\text{Horizontal Distance} = \text{Slope Distance}\cdot \text{Cos}(\text{slope angle})[/latex]




Then, we can calculate the total height of the tree by using the angles we measured to its top and bottom.




[latex]\text{Tree Height}= \text{Horizontal Distance}\cdot (\text{Tan angle to top - Tan angle to bottom})[/latex]




We can put these together into one equation.




[latex]\text{Tree Height}= \text{\text{Slope Distance}\cdot \text{Cos}(\text{slope angle})}\cdot (\text{Tan angle to top - Tan angle to bottom})[/latex]




Measurements in Percent


When measuring in the height of an object using the percent scale, find the horizontal distance from the object.




HD = SD * \cos(\tan^{-1} \frac{slope}{100})




Use this in the calculation for height.




([latex]Height= (%T-%B)*HD[/latex]).




The formulas can also be combined into one calculation.




[latex]Height= (%T-%B)*SD * \cos(\tan^{-1} \frac{slope}{100})[/latex]




Forest Measurements by Joan DeYoung has a great discussion and explanation of the arithmetic for working with percent slope!






Examples: Heights on Slopes






A) Find the height of this tree.




View answer.


Watch solutions video.






 


Gaps


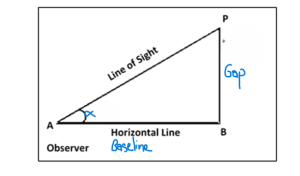
You’re on one side of a river (or a canyon, or a swampy muskeg, or a busy highway) and need to know the distance to the other side. Right triangles can help and it’s like surveying magic!


Any gap (like a river) can be dealt with by finding an object on the opposite side that you can sight 90 degrees from parallel to the gap.


You’ll need to know one of the legs of the triangle and one of the angles. Which ones can you readily measure?


Use a tape to measure the distance you walk from the object you sighted on the other side to the point you’ll sight back to the object (side b). Use a compass to measure angle α. Viola! You have an angle and a side of a right triangle. Use these to find side a.




[latex]Gap (a) = baseline (b)* \tan\alpha[/latex]




(In this particular diagram, you’d need to subtract the distance you stood from the river’s edge from a to get the width of the river.)


In general, we call side b the baseline and angle α is our “angle to point“.






Examples: Measuring Across Gaps






A) I’m measuring across a gap. I set up a baseline of  50′ and measure α an “angle to point” back to the object I sighted on as 21°. What is the distance across the gap?


B)  The gap in this sketch is a canyon. Point P is a giant pine on the other side. Your baseline is 100 feet and your angle to point (α) is 34°. What is the distance across the canyon?




View answers.


Watch solutions video.






Gaps on a Slope


If you’re working on a slope and measuring across a gap, you’ll need to correct for the slope to find the true baseline before running your calculations. To find the accurate baseline use [latex]HD = SD * \cos(\tan^{-1} \frac{slope}{100})[/latex] if you measured slope in percent and [latex]\text{Horizontal Distance} = \text{Slope Distance}\cdot \text{Cos}(\text{slope angle})[/latex] if you measured slope in degrees.


 






Examples: Measuring Across Gaps on a Slope






      A) You’re on a mountainside next to a waterfall and you want to know how wide the river is at the falls. There’s a big pine on the other side of the waterfall. You stand across from the pine and then turn 90º and walk 200 feet down the slope. You sight back to the pine at an angle of 5º from your baseline. Then, you remember: The baseline you walked down the slope won’t be a true horizontal distance because the mountainside is so steep. If you want your measurement of the waterfall to be accurate, you need to take the distance you walked (200 ft) and correct it from a slope distance to a horizontal distance. You use your clinometer and measure the slope angle as 4º. Now – use the true horizontal distance for the baseline and calculate the width of the waterfall.




      View answer.


      Watch solutions video.




Plots on a Slope


Similarly, when you are putting in plots, you’ll use the corrected horizontal distance if you are measuring up or down the slope. The distance you measure on the ground along the plot’s radius will be the slope distance (SD) and you’ll need to find the horizontal distance (HD) to calculate the plot area.


 


To set up uniform plots, we’ll use the same horizontal distance for the radius of each.






Examples:  Plots on a Slope






A) Your plot radius needs to be 30 feet, but you’re on a slope of 5%. What should the length of the radius be up and down the slope?


B) You are putting in square quadrats on a steep slope of  22%. How long should the side oriented downslope be?


View answer.


Watch solutions video.






 


 






Problem Set 8.4








1)  Point A is at 1500′ and Point B is at 1950′. The distance between them on a 1:24000 scale map is 3.25 inches. What is the slope between these points in percent? What is the slope in degrees?


2) Your 1:24000 – scale map has contour lines at 20′ intervals. If you count 4 contour lines between the landing and your harvest area and the distance is 1.125 inches. What is the average slope between these areas? In percent? In degrees?


3) My very accurate pedometer says I walked 1 mile straight up Mt. Spokane. I started at 4,800 feet elevation and ended at 5,887 feet. What is the average slope for this hike?


4) My ladder is 28′ tall. If I stay within the safe bounds, how far away can I set its base away from a wall I am painting?


5) How long does my ladder need to be to safely access a 16-foot roof? Include an extra three feet for your ladder to extend above the roof height.


6) Our porch is 18 inches tall and we need to build a ramp so Grandma can come stay with us. How long will the ramp need to be to meet ADA guidelines?


7) What is the average slope (in percent) of a trail that gains 800 feet in 3 miles?


8) My trail needs to maintain an average slope of  20% and climb from the parking area at 500 feet elevation to a lookout at 1200 feet elevation. How long will the trail be (slope distance)?


9) What is the average slope of a trail that gains 50 meters over 1 kilometer of walked distance (slope distance)?


10) Find the heights of the trees measured on level ground.






Angle to top of tree
Angle to base of tree
Distance from base




42%
-5%
50 feet




28%
-2%
100 feet




61%
-10%
75 feet




50°
-2°
66 feet




38°
-5°
200 feet




71°
-4°
100 feet








11) You’re on a slope of 6° and standing 66 feet downhill from a large Ponderosa pine. You sight 18° to the top of the tree and 2° to the bottom. What is the height of the tree?


12) You’re on a slope of 9° and standing 100 feet uphill from a large western larch. You sight 5° to the top of the tree and -12° to the bottom. What is the height of the tree?


13) Find the heights of the trees measured while sighting up or down a slope.






Angle to top
Angle to base
Slope
Distance from tree up or downslope (slope distance)




50%
3%
12%
100 feet




-2%
-40%
20%
100 feet




62%
5%
18%
50 feet




12%
-15%
22%
150 feet




80%
10%
25%
66 feet




30°
2°
10°
100 feet




-10°
-32°
45°
50 feet




67°
2°
20%
100 feet




25°
-12°
12%
100 feet








14) I’m measuring across a gap. I set up a baseline of  200′ and measure α an “angle to point” back to the object I sighted on as 18°. What is the distance across the gap?


15) You’re on the edge of the Spokane River Canyon near Riverfront Park. You sight  from the edge of the canyon on the Centennial Trail across to a townhouse in Peaceful Valley. Then, you turn 90º and walk 300 feet parallel to the canyon. The walk has no appreciable slope. You turn and sight back to that townhouse. The angle from your baseline back to the townhouse is 44º. How far is the gap across the canyon to the townhouse?


16) Find the distances across these gaps.






Baseline (slope distance)
Angle to point
Slope along baseline




500 feet
24°
0%




250 feet
42°
0%




100 feet
19°
15%




500 feet
12°
20°






17) Your plot radius needs to be 60 feet, but you’re on a slope of 20%. What should the length of the radius be up and down the slope?


18) You are putting in square quadrats on a steep slope of  30%. How long should the side oriented downslope be?


19) The downward grade of the ground from my house out toward the shed is 2%. If the shed is 100 feet horizontally from the base of the house, how much lower is the ground at that point?


20) SD = 122 ft’ Slope Angle = 5° Find HD and VD.


21)  Slope Angle = 12° HD = 100 ft  Find SD and VD.


22)  HD = 120 ft VD = -8 ft   Find SD and Slope Angle.


23) You measure a distance of 197.3 feet on a slope of -27° 15’13”. Find the horizontal and vertical distances in feet to the nearest tenth of a foot.


24) A plot radius of 27.4 feet is laid out on a map. The slope is 16°. Find the length of the radius on the ground.


25) Two points on a map are 5.4 inches apart. The scale is 1:24000.  The starting elevation is 1,200 feet and the ending elevation is 1,450 feet. (a) Calculate the distance between the two points on the map in feet to the nearest foot. (b) Find the angle of the slope. (c) Calculate the distance if measured on the ground.








definition





					
		
					

						

							

								
License

								
Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License
8.7 Triangles are the Answer! Solving Applied Problems Copyright © by Bob Brown; Morgan Chase; and Marilyn Nielson is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.
							

														

								
Share This Book