13 Perimeter and Circumference
Learning Objectives
- Find perimeter and circumference
- Determine the perimeter and circumference formulas for common figures
Find Perimeter and Circumference
The perimeter of a shape is the distance around the outside of the shape.
When the shape is a circle, we call this distance the circumference.
Examples: Write the formula for the perimeter or circumference of the common shapes below each.
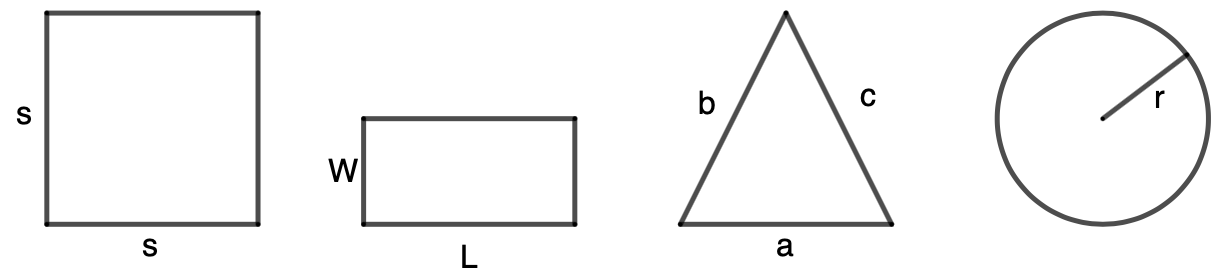
Solutions:
Square: P = 4s. Rectangle: P= 2W + 2L. Triangle: P = a + b + c. Circle: P = [latex]2\pir[/latex]
Even though you can write "formulas" for some basic geometric shapes- you should not try to memorize these formulas- rather you should try to understand that to compute the perimeter of a shape, means add up all of the lengths of the shape.
Exercises
- The length of a square field is 187 yards. Create a diagram and find the perimeter.
Solution: 
![]()
2. If a rectangular field has a perimeter of 400 ft and a width of 73 ft, find the length of the field. Use a diagram.
Solution:  .
. ![]()
3. Suppose that a rectangular field has a total perimeter of 196 ft. If the length of the field is 5 more than twice the width, what are the dimensions of the field?
Solution: 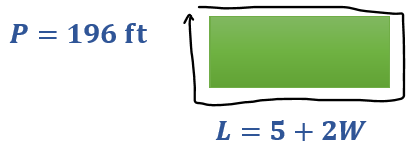
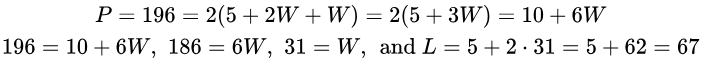
4. What is the circumference of a circular garden if the distance across the middle is 20 ft. Use 3.14 for pi.
Solution: ![]()
When finding the perimeter of irregular figures, you can deconstruct the figures into shapes that you understand how to find the perimeter of, such as those above. If you divide up a shape though, be sure to only count the sides that are on the outside.
Exercises: Find the perimeter of the following shapes.
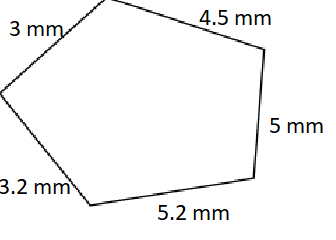
Solution: ![]()
2.
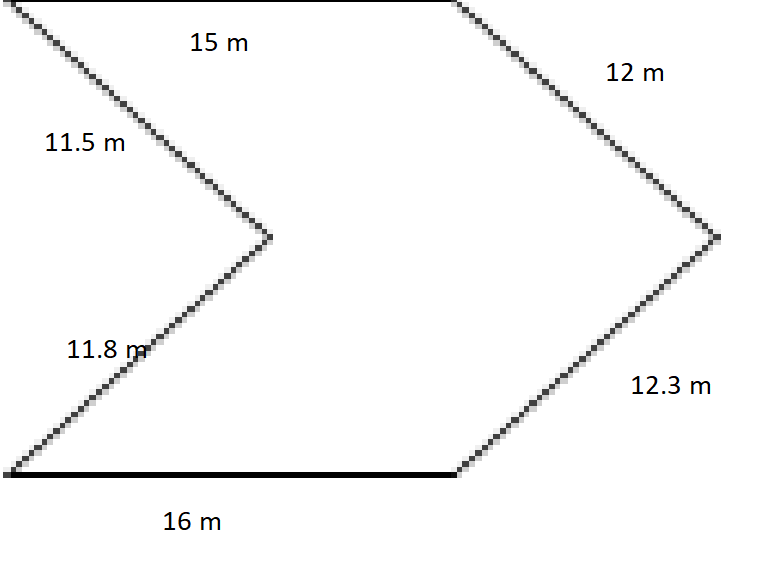
Solution:![]()
3.
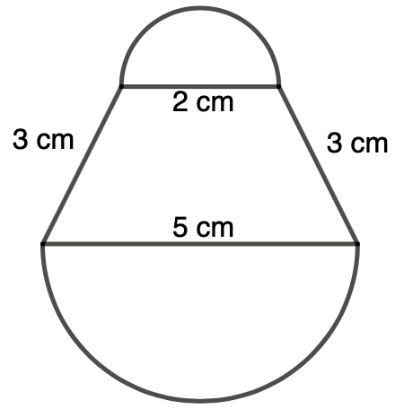
Solution: This figure consists of two semicircles of different sizes plus two 3 cm connections on the outside. So, we need to find half the circumference of each circle (the circumference of the circular portion of the semicircles) and add 6 cm to those values.
Smaller circle has a diameter of 2 cm, so C = 1/2 •2 • 3.14 = 3.14 cm. The larger circle has a diameter of 5 cm, so C = 1/2 •5 • 3.14 = 7.85 cm. Thus, the perimeter of the entire figure is 3.14 + 7.85 = 16.99 cm.
4.
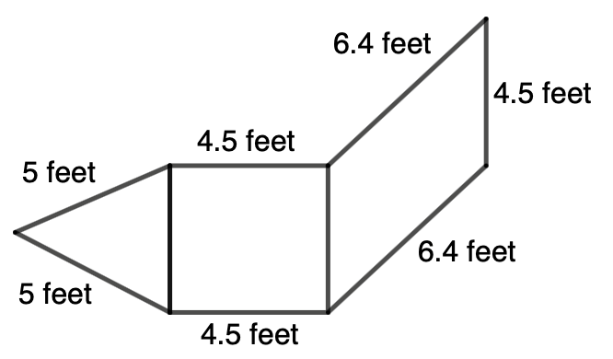
Solution: ![]()
Attributions
- Content and images, except where otherwise noted, adapted from "MATH 1420: Geometry Concepts for Teachers" by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 International License.

