14 Area of Planar Figures
Learning Objectives
- Determine the area formulas for basic planar figures
- Find area of polygons and circles
- Find the area of irregular figures made up of polygons or circles.
Finding Area
The Area of a shape is the measurement of the space occupied by the shape.
Examples: Write the formula for the area of the shapes below.
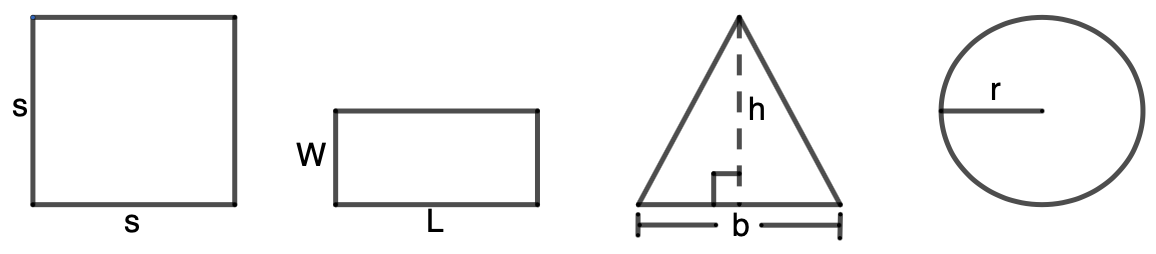
Square: [latex]A = s^2[/latex].
Rectangle: [latex]A = L W[/latex]
Triangle: [latex]A = \frac{1}{2} b h[/latex]
Circle: [latex]A = \pi r ^2[/latex]
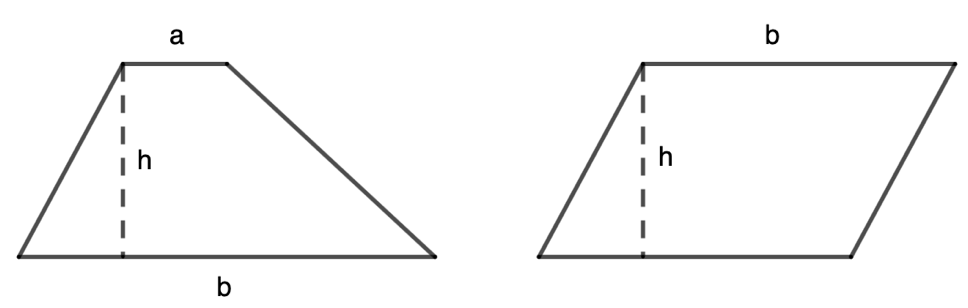
Parallelogram with unequal bases: [latex]A = \frac{1}{2} h (a + b)[/latex]
Parallelogram with equal bases: [latex]A = b h[/latex]
*Notice that if a = b in the above parallelograms, then (a +b) = 2a. Replacing this in the equation for unequal bases then matches the equal base equations.
Note: Area is always measured in square units.
We can use the above formulas to find area of some basic shapes, as in the examples below.
Examples: Find the area of the basic figures below.
- Find the area of the trapezoid below.
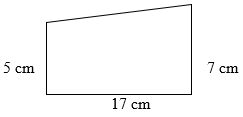
Solution: Using the area formula for a trapezoid.... 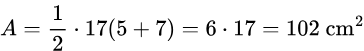
2. Find the area of a circular plot of land with diameter 240 meters.
Solution: 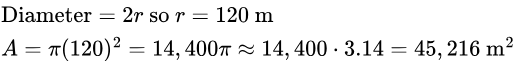
To find the area of more irregular figures, it is often necessary to break up the shape into sub-shapes and find the area of each shape in the deconstruction. This is done in the examples below.
Example: Find the area of the irregular shape.
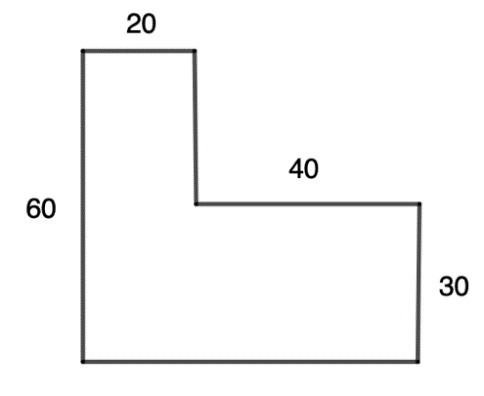
Solution: We can see that if we drop the right side of the upper portion straight down we get two rectangles as shown.
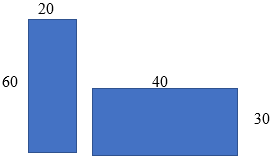
So, we have
for the left rectangle and
for the right rectangle. Thus, we have
square units. Note that area is shown in square units.
This same strategy can be done for shapes involving circles as well!
Example: Find the area of the partial circle if the angle in the center is a right angle and the radius is 5 units.
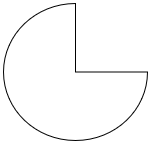
Solution:

What basic shapes make up the "arrow" shape below?
Examples: Find the area of the figure. The height of the triangular portion is 2 units.
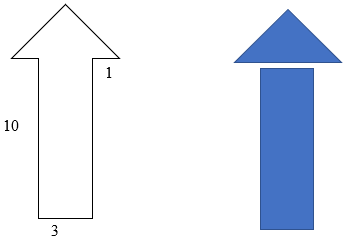
Solution:
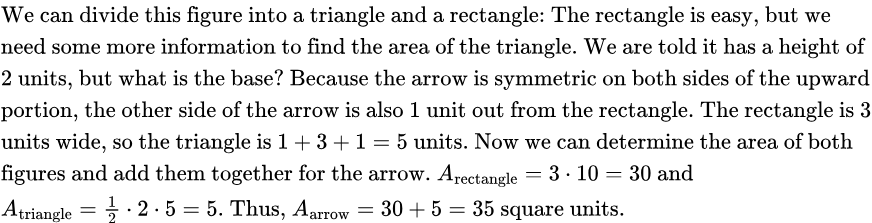
If your shape is on a grid (that is, horizontal and vertical lines making up unit squares), then you can compute the area by counting how many full squares the shape covers. You can also use the grid to better break up or decompose the shape into simpler shapes.
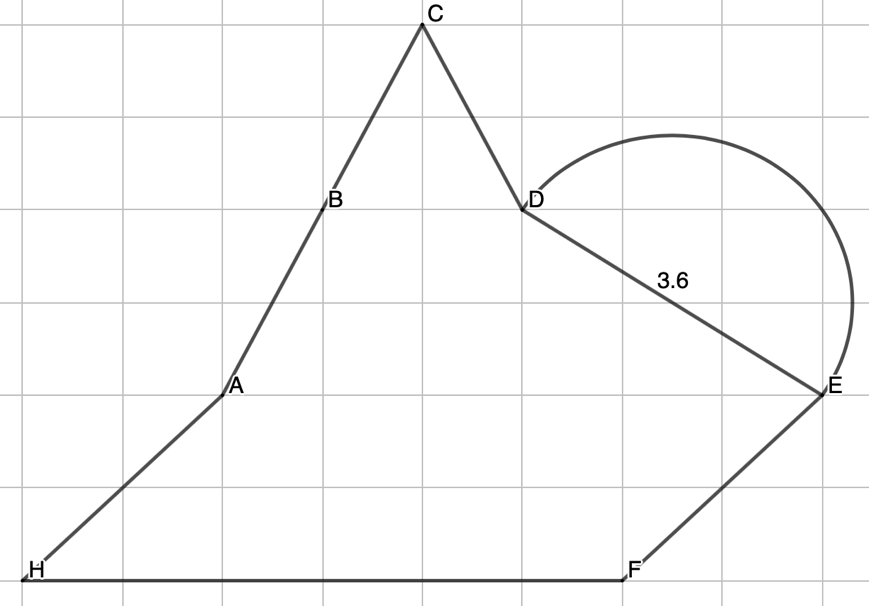
Example: Assume the grid lines are one unit apart. Find the area.

Attributions
- Content and images, except where otherwise noted, adapted from "MATH 1420: Geometry Concepts for Teachers" by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 International License.

