1 Translations and Rotations
Learning Objectives
- Understand and use translations
- Understand and use rotations
A one-to-one correspondence between a plane and a copy of the plane is a transformation. Transformations can be thought of as a function from a plane to itself- and as such, transformations have properties of functions.
We are going to look at several types of transformations in this chapter. The two that we look at in this lesson are translations and rotations.
Translations
A translation, or slide, is a motion of a plane that moves every point of the plane a specified distance in a specified direction along a straight line, resulting in the following:
- A figure and its image are congruent.
- The image of a line is a line parallel to it.
A translation is a function from the plane to the plane such that every point (x, y) gets mapped to the point (x+a, x+b), where a and b are real numbers. This can be written symbolically as
[latex](x, y) \rightarrow (x + a, y + b)[/latex]
where "→" denotes "moves to."
Any rigid motion (e.g., transformation) that preserves length or distance is an isometry. A translation is a type of isometry.
Example
Below is an example of a translation of a rectangle ABCD in the plane to a new positions A'B'C'D' on the plae but with the length and shapre of each part of the retangle maintained. The slide is represented by the arros. A slide arrow, [latex]\rightarrow[/latex], for A to A' indications you would move point A to A' and slide each of the other points in the same direction for the same distance.
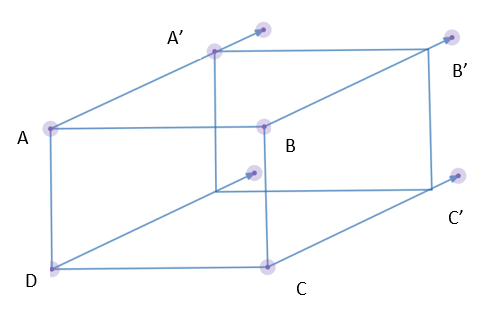
There are two methods to indicate how to move your translation in an xy-plane.
- By specifying the amounts (a, b) to shift each (x,y).
- By specifying the direction and amount to shift each point.
Practice Exercises
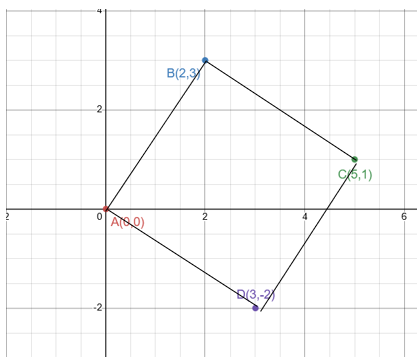
- Write and plot the coordinates of the image of the vertices of a quadrilateral ABCD under the translations in parts a and b.
![]()
b.
Solution: a. [latex](x, y) \rightarrow (x -2, y +4)[/latex]. b. [latex]A(0,0) \rightarrow A'(1, -2)[/latex]
2. For the quadrilateral below, find its image under a translation from points A to B.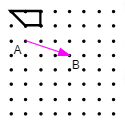
Rotations
A rotation is a transformation of the plane determined by rotating the plane about a fixed point, the turn center or center of rotation, by a specific amount in a specific direction (a certain number of degrees either clockwise, negative degrees, or counterclockwise, positive degrees). The following shows three different rotations of the triangle, ![]()
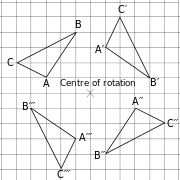
Practice Exercise
3. The image of [latex]\bar[/latex] under a rotation is given in the following figure. Find the original line [latex]null[/latex][latex]\bar{AB}[/latex]
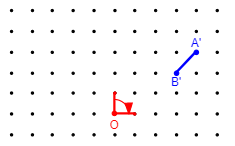
A rotation of 360o about a point moves any point and hence any figure onto itself. Such a transformation is an identity transformation. Any point may be the center of such a rotation.
A rotation of 180o about a point is a half-turn. The direction of the rotation does not affect the results in either the identity transformation or the half-turn.
Practice Exercises
4. For the points (3, 0) and (-2, 2) find the coordinates of the image point under a half-turn about the origin. On your graph, plot the original points in one color and the images in a different color.
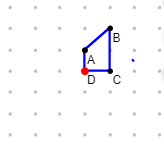
5. Find the image of the quadrilateral to the right in a 270 degree clockwise rotations about D. Hint: Start with one point and rotate it 270 degrees, then rotate a different point until you have rotated all four of the vertices of the quadrilateral.
Attributions
- Content and images adapted from "MATH 1420: Geometry Concepts for Teachers" by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 International License.

