2 Reflections, Glide Reflections, and Dilations
Learning Objectives
- Understand and use reflections
- Understand and use dilations
Reflection
Another type of isometry is a reflection. The most common example of a reflection often encountered in our daily lives is our image in a mirror.
Definition.
A reflection in a line [latex]\ell[/latex] is a function of a plane that matches up each point A of the plane with a point A' in such a way that [latex]\ell[/latex] is the perpendicular bisector of AA', for A not on [latex]\ell[/latex]. If A is on [latex]\ell[/latex], then A = A'. This definition is illustrated below"
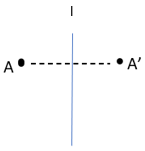
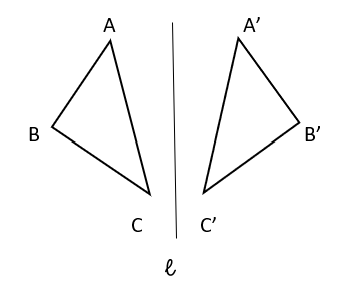
We can obtain reflections about a line in various ways. Folding the paper along the reflecting line(in blue) and drawing the image gives the mirror image, or image, of the figure.
Tracing paper can be used. Trace the original figure, the reflecting line, and a point on the reflecting line, which we use as a reference point, first picture. Flip the tracing paper over to perform the reflection, and align the reflecting line and the reference point, second picture.
Reflections in a Coordinate System
For some reflecting lines, the x-axis, y-axis, and y=x line, it is quite easy to find the coordinates of the image, given the coordinates of the point.
Example- Reflection over the line y = x
The image of A(3, 5) is A'(5, 3).
The image of B(-4,0) is B'(0, -4).
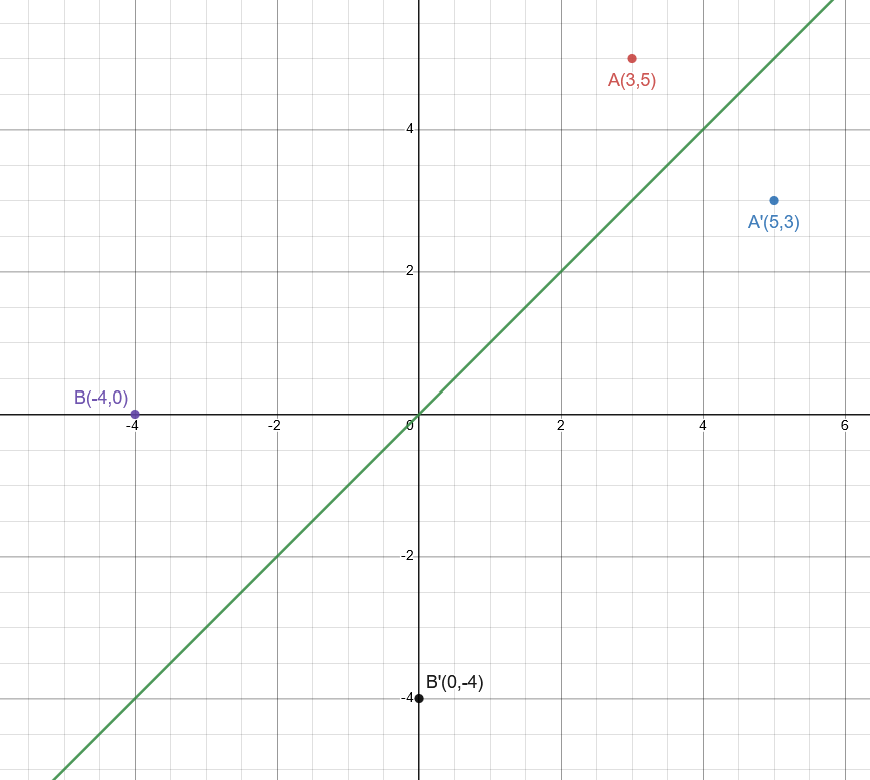
In general: Under the reflection over the line y = x, a coordinate point (s, t) goes to the point (t, s).
Practice Exercises

Solution: The image is the same as the preimage.
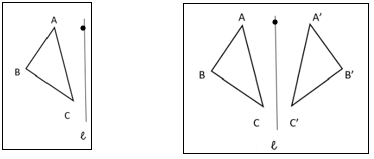
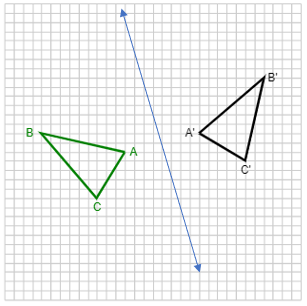
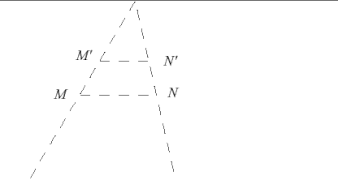
2. Given [latex]\triangle ABC[/latex] and its reflection image [latex]\triangle A'B'C'[/latex] find the line of reflection. Draw the line of reflection on the graph.
Solution: Using a tape measure or ruler, show that the distance from A perpendicular to the line is the same as the distance from A’ perpendicular to the line. Do the same with B and B’, C and C’.
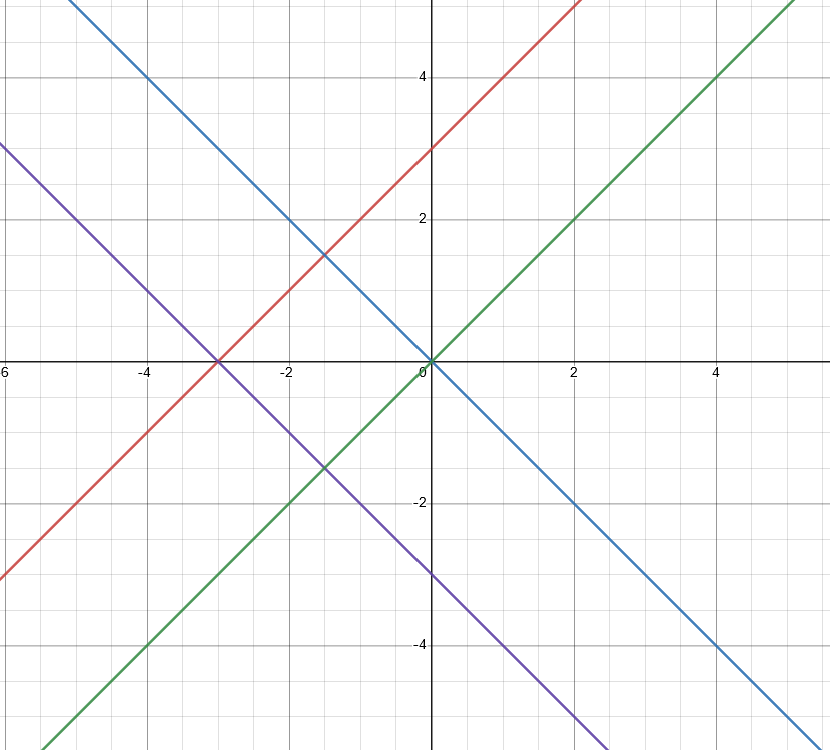
3. Find the equation of the images of the following lines when the reflection line is the x-axis.
a. y = x+3
- Solution: Red line
b. y= -x
- Solution: Blue line
Reflection of equation a is y= -x -3, (purple line)
Reflection of equations b is y = x (green line)
Glide Reflection
A glide reflection, another basic isometry, is a transformation consisting of a translation (green arrow), followed by a reflection in a line (blue arrow) parallel to the slide arrow (orange arrow).
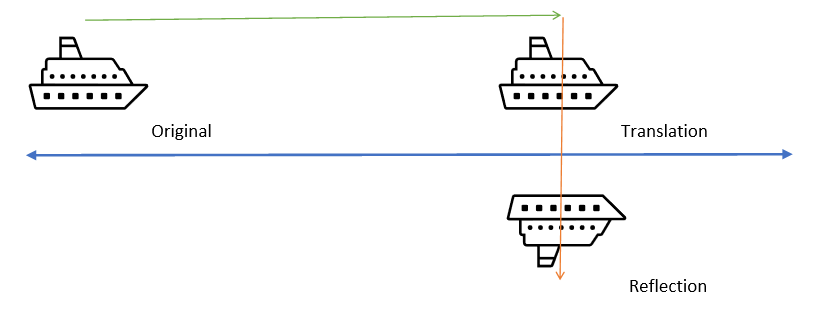
Thus the boat is moved forward and flipped over.
Dilation
A dilation is a transformation that resizes the object, smaller to a reduction or larger to an enlargement. The scale factor represents the amount of the resizing.
Below are two examples of images of a dilation. Sometimes a point outside the object (e.g., O in the dilation on the left below) is used to assist in the alignment. The diagram on the right uses the xy-coordinate plane to correctly line up the enlargement (red triangle to blue triangle) or reduction (blue triangle to red triangle). Can you find the scale factor for both of these dilations?
O
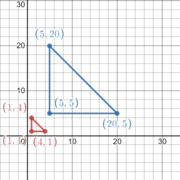
The enlargement has a scale factor of 5, and the reduction has a scale factor of 1/5.
Examples
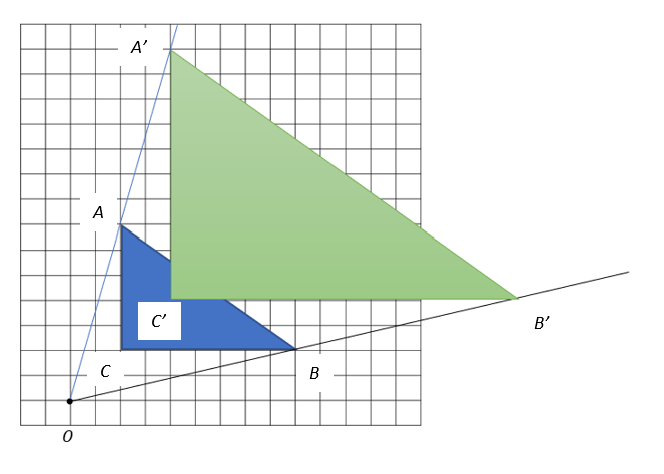
4. In the following drawing, find the image of triangle ABC under the dilation with center O and scale factor 2.

Attributions
- Content and images, unless where otherwise noted, adapted from "MATH 1420: Geometry Concepts for Teachers" by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 Internantial License.
- Other images:
- "Dilatation_avion.gif" image by Robert FERREOL, Wikimedia Commons, Public domain, https://commons.wikimedia.org/wiki/File:Dilatation_avion.gif.

