7 Euclidean Geometry
Learning Objectives
- Understand the axioms and postulates of Euclid
- Use these to prove additional theorems about geometric figures
Axioms and Postulates
Certain terms need to be defined so we can understand how they were used by Euclid of Alexandria, a Greek mathematician who lived around 300 BCE. He established the ideas and rules we now use in elementary and high school geometry. His book The Elements, is actually composed of 13 books and discusses geometry, number theory, sequences and much more.
An axiom is a self-evident or universally recognized truth.
A postulate is an assertion of a truth or something that is assumed as true.
A theorem is an idea or statement that has been proven true.
The Axioms and Postulates of Euclid are given here in the version presented by Sir Thomas Heath (1861-1940) in The Elements of Euclid. (1908) instead of Euclid’s original.
Euclid’s Axioms
- Things which are equal to the same thing are also equal to one another.
- If equals be added to equals, the wholes are equal.
- If equals be subtracted from equals, the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
Euclid’s Postulates
- A straight line can be drawn between any two points
- A straight line can be extended indefinitely in a straight line.
- A circle can be drawn with any center and any radius.
- All right angles are equal to one another (i.e., congruent).
- If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the straight lines, if produced indefinitely, will meet on the side on which the angles are less than two right angles. In other words, parallel lines exist.
The postulates are illustrated geometrically below.
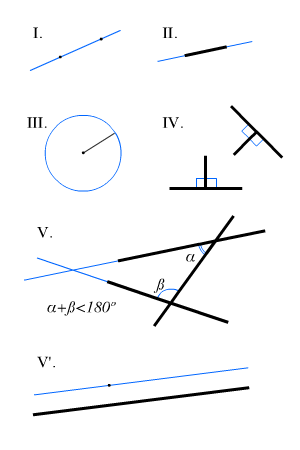
An alternative version of the Fifth Postulate was presented by John Playfair in 1795. This version is more easily understood and is often referred to as the Parallel Postulate.
The Parallel Postulate
Through a given point P not on a line L, there is one and only one line in the plane of P and L which does not meet L.
The Parallel Postulate is illustrated in V’ in the diagram above, with the black line being line L, the black point being P and the blue line is the one and only one line which does not meet line L.
This fifth postulate cannot be proven as a theorem though many have tried. So, Euclid said these postulates are assumed to be true, and did not attempt to prove them. But he used these axioms and postulates to prove Propositions (Theorems). Once a Theorem has been proven using these ten assumptions, it can then be used to prove any successive theorem.
In The Elements, Euclid proved 465 such theorems. He also used constructions using only a straightedge and compass.
Use the axioms and postulates to prove the following:
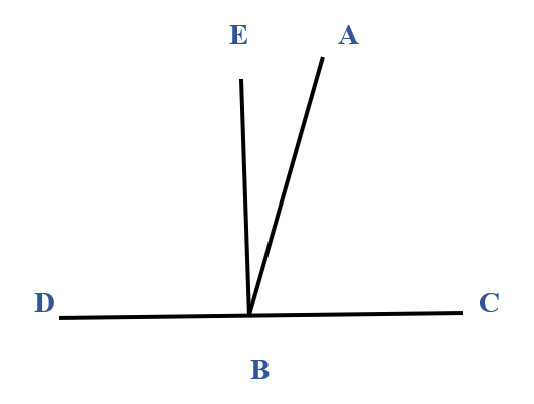
If a straight line stands on a straight line, then it makes either two right angles or angles whose sum equals two right angles.
Let any straight line AB standing on the straight line CD make the angles CBA and ABD as illustrated below.
We will show that either the angles CBA and ABD are two right angles or their sum equals two right angles (180
).
Proof:
Now, if the angle CBA equals the angle ABD, then they are two right angles (by definition).
But, if not, draw BE from the point B at right angles to CD. Therefore, the angles CBE and EBD are two right angles (by construction and definition).
Since the angle CBE equals the sum of the two angles CBA and ABE, add the angle EBD to each, therefore the sum of the angles CBE and EBD equals the sum of the three angles CBA, ABE, and EBD (by Axiom 2).
Again, since the angle DBA equals the sum of the two angles DBE and EBA, add the angle ABC to each, therefore the sum of the angles DBA and ABC equals the sum of the three angles DBE, EBA, and ABC (by Axiom 2).
But the sum of the angles CBE and EBD was also proved equal to the sum of the same three angles, and things which equal the same thing also equal one another (Axiom 1), therefore the sum of the angles CBE and EBD also equals the sum of the angles DBA and ABC. But the angles CBE and EBD are two right angles, therefore the sum of the angles DBA and ABC also equals two right angles (180
).
Therefore if a straight line stands on a straight line, then it makes either two right angles or angles whose sum equals two right angles.
Content created in 2022 by the Math 1410/1420 OER Team. This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
- https://commons.wikimedia.org/wiki/File:Euclid%27s_postulates.png
