9 Pythagorean Theorem and Congruent and Similar Triangles
Learning Objectives
- Understand the Pythagorean Theorem
- Use the Pythagorean Theorem
- Discover Congruent and Similar Triangles
- Use the Concepts of Congruency and Similarity of Triangles
Pythagorean Theorem (revisited)
The Pythagorean Theorem: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other legs. In other words, using the diagram below, we have the following relationship: [latex]c^2 = a^2 + b^2[/latex].

You can use the Pythagorean theorem to find missing side lengths in triangles or other shapes that are made up of right triangles. The following example problems use the Pythagorean Theorem.
Examples
1. A baseball diamond is square. Each side of the square is 90 feet long. How far is it from home plate to second base?
(a)Draw a diagram of this scenario, complete with labels:
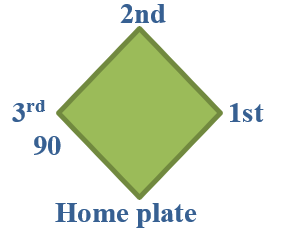
(b)Use the Pythagorean Theorem to find the distance from home plate to second base, both in exact form and rounded to the nearest tenth:
Since this is a square, at first base, we have a right angle and the distance from home plate to second base is the hypotenuse of a right triangle. Now each side is 90 feet and they are both the a and the b in the Pythagorean Theorem.
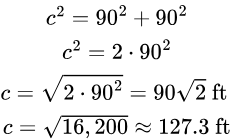
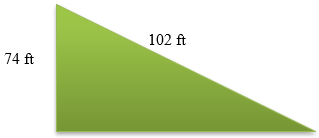
2. Use the Pythagorean Theorem to find the unknown side of a triangular park which has the following shape. Round to the nearest foot.
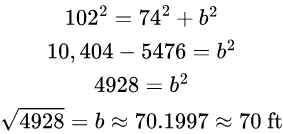
Congruent and Similar Triangles
In general, the word congruent means “coinciding exactly when superimposed”. This means that two shapes are congruent when, if you put one exactly on top of the other, all parts align. The formal definition for congruent triangles is given below.
Definition: Two triangles are congruent if each pair of corresponding angles have the same measure and each pair of corresponding sides are the same length. The following cases indicates how to determine if two triangles are congruent.
Criteria for Determining Congruent Triangles:
The following three situations are ways you can determine if two triangles are congruent.
Angle-Side-Angle (ASA): Two triangles are congruent if two of the angles are equal and the lengths of the corresponding sides between the angles are equal.

Angle-Angle-Side (AAS): Two triangles are congruent if two angles and a side (not the side between the two angles) are congruent.
Side-Side-Side (SSS): Two triangles are congruent if the lengths of the corresponding sides are equal.
When drawing congruent shapes, we need to indicate the corresponding congruent parts. This is done by using curves on angles or dashes on sides.
For angles, the single, double, or triple curves on the angles show which angles are congruent as shown in this diagram.
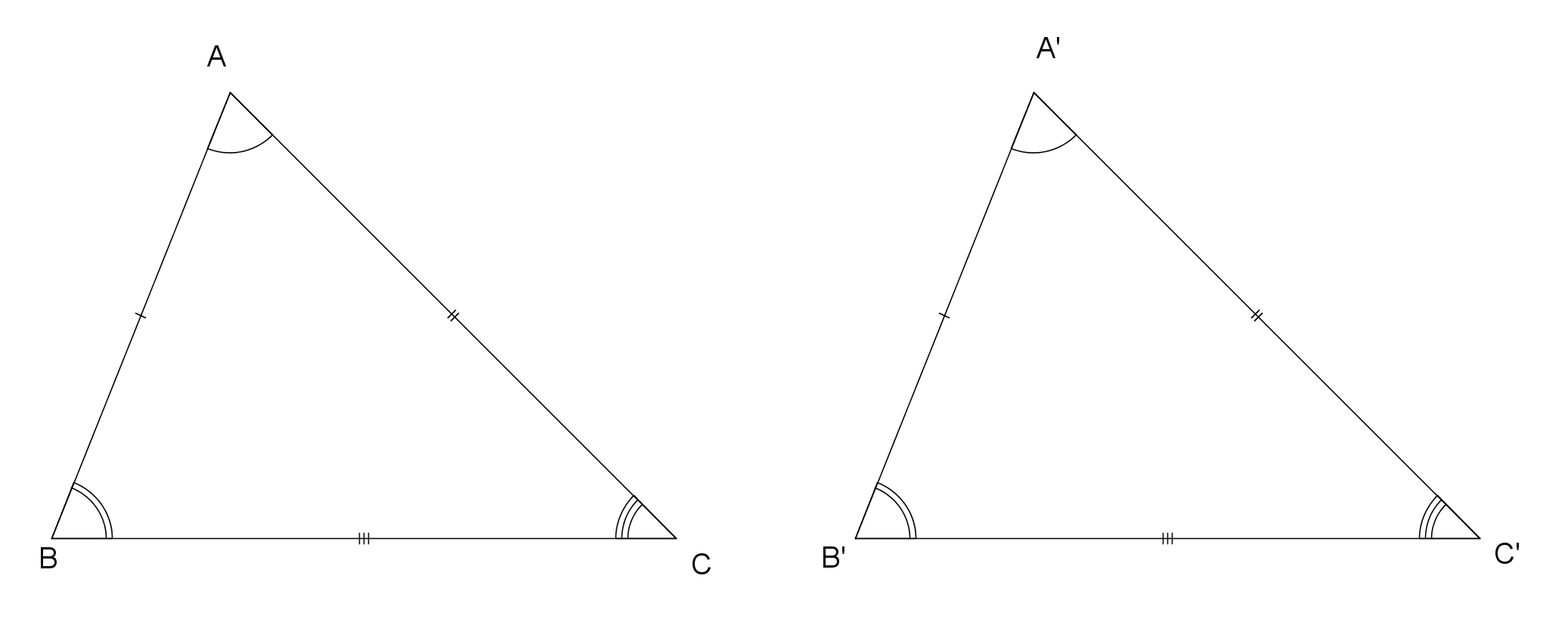
For sides, single, double, and triple dashes on each side of the trapezoid indicate which sides are congruent.
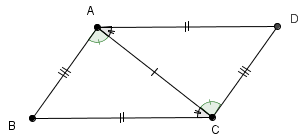
Examples- Congruent triangles in the world.




Similar Triangles
In contrast to congruent triangles- in which all corresponding parts (angles and sides) are equal, similar shapes are shapes that look the same but may be scaled versions of each other. The formal definition for similar triangles is given below.
Definition: If two triangles are similar, then their corresponding angle measures are equal, and their corresponding side lengths are in the same proportion.
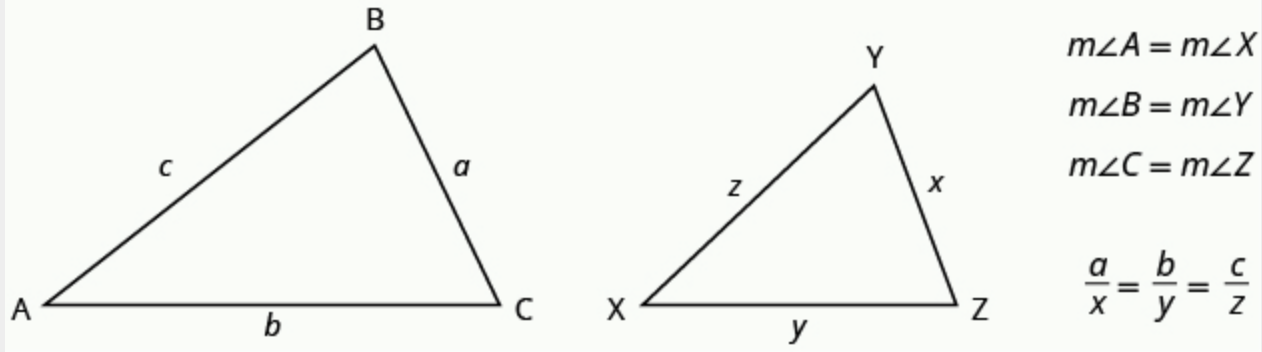
Note: the relationship [latex]\frac{a}{x} = \frac{b}{y} = \frac{c}{z}[/latex] is used to help determine side unknown side-lengths of similar triangles (see the Examples below).
Criteria for Determining Similar Triangles:
Angle-Angle (AA): Two triangles are similar if two of the corresponding angles are equal.

Side-Side-Side (SSS): Two triangles are similar if the lengths of all three sides of each triangle are proportional.

For the triangles above triangles, each side of the second triangle is three times the length of the corresponding side of the first triangle (in other words, each side of the first triangle is 1/3 the size of the corresponding side of the triangle on the right). Three (or 1/3) is called the scale factor.
Side-Angle-Side (SAS): Two triangles are similar if two corresponding sides are proportional and the angles between the two sides are equal.

The angles between the labeled sides are the same, and the sides of the second triangle are 3/2 the size of the corresponding sides of the first triangle.
Examples
Examples: The triangles below are similar. Find the length of the unknown angles and sides of each. Round angles to the nearest degree and sides to the nearest tenth.
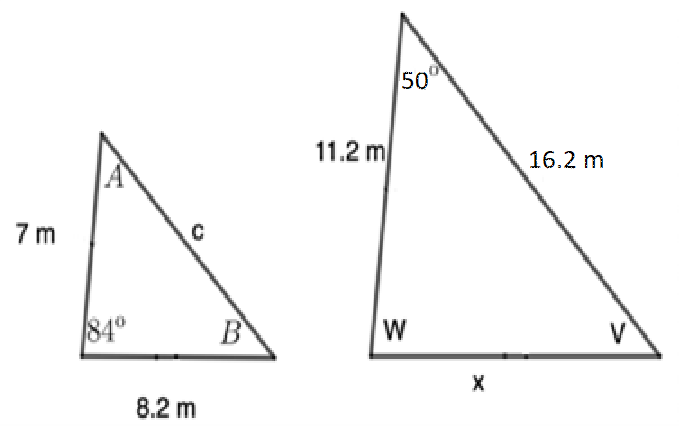
Solution:
Since the triangles are similar, we know that all corresponding angles are equal. This means [latex]\angle A = 50^o[/latex] and [latex]\angle W = 84^o[/latex]. Next, since the angles in a triangle add up to [latex]180^o[/latex], we can compute the measure of the third angle in each triangle. In particular, we need to have [latex]50^o + 84^o + \angle V = 180[/latex]. Solving for [latex]\angle V[/latex] gives us [latex]\angle V = 46^o[/latex].
To compute the side lengths, we need to determine the scale factor between the two triangles. Since corresponding sides of 7m and 11.2 m are given, we see that [latex]\frac{7}{11.2}[/latex] is the relationship between each corresponding side lengths. Thus we have:
[latex]\frac{7}{11.2} = \frac{8.2}{x} = \frac{c}{16.2}.[/latex]
Solving for [latex]x[/latex] and [latex]c[/latex] gives us,
[latex]x \approx 13.2[/latex] and
[latex]c \approx 10.125[/latex].
2.
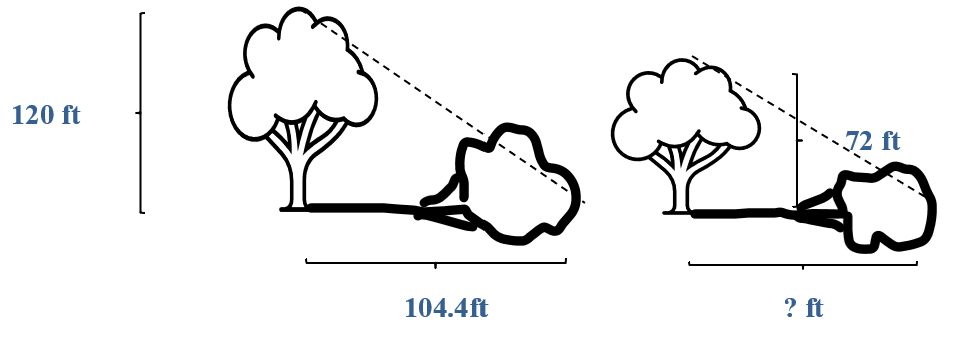
Similar triangles provide a way to find the height of tall objects, such as statues, flagpoles, or trees. At any moment during the day, the sun's rays cast the same angle between the ground and an object (such as a tree). This means that the "triangles" formed from a tree (or flagpole, etc), the shadow that is cast, and the point from the top of the shadow to the top of the object form similar triangles.
A 120-foot tall tree casts a 104.4-foot shadow. How tall is a tree that casts a 72-foot shadow?
Solution: Since the triangles are similar (as explained above) we can use the proportions between corresponding side lengths to find the missing values.
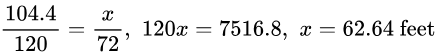
3.
A 6-foot tall man casts a shadow of 10 feet. How tall is a tree which has a 90 ft shadow measured at the same time?
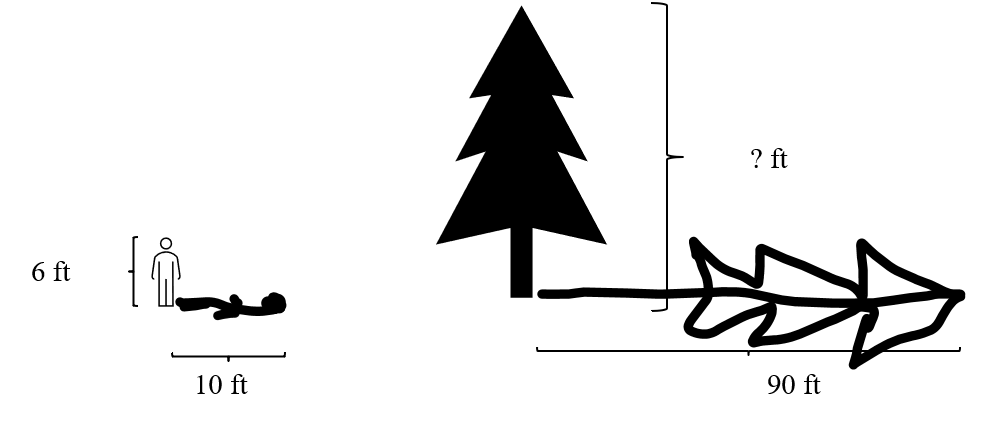
Solution: Similar to the Example 2 above, we set up and solve an equation using the proportions in the triangles.
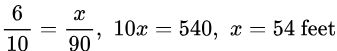
Attributions
- Content and images, except where otherwise noted, adapted from "MATH 1420: Geometry Concepts for Teachers" by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 International License.
- Some diagrams were obtained from Wikimedia Commons:
- ASA Triangle Congruence, Somebody762, CC BY-SA 3.0
- SAS Triangle Congruence, Somebody762, CC BY-SA 3.0
- Geodesic-wooden-dome, El Paso, La Palma, Originalausgabe, Public Domain
- A periodic tiling by regular hexagons and equilateral triangles, Baelde, CC BY-SA 3.0
- Star of David, Zscout370, Public Domain
- Beer garden patio umbrella, Black Horse, Nuthurst, West Sussex, England, Ethan Doyle White, CC BY-SA 4.0
- Triángulos congruentes, Vinícius Weite Thomé, CC BY-SA 4.0
- Lados opostos congruentes, Werneck Dorneles da Silva, CC BY-SA 4.0
Media Attributions
- Pyth Thm
- Screenshot 2025-02-27 at 9.18.55 AM
- Screenshot 2025-02-27 at 9.19.03 AM
- Screenshot 2025-02-27 at 9.19.11 AM


