18 Complements and Single Trial Conditional Probability
Learning Objectives
- Find probabilities using the law of complements
- Find single trial conditional probabilities
Complements
Let S denote the sample space of a probability experiment and let E denote an event. The complement of event E, denoted EC, is all outcomes in the sample space S that are not outcomes in the event E.
Examples: Complement
Let the event E be rolling a number less than 3 on a 6-sided die.
- What is the sample space?
- Solution:
- The sample space is all possible outcomes when you roll the 6-sided die.
- Solution:
- What outcomes are E and EC?
- Solution: E = {1, 2} and EC= {3, 4, 5, 6}
- Since E is rolling a number less than three- that includes the numbers 1 and 2. The complement of E must be rolling a number 3 or larger! These numbers and 3, 4, 5, and 6.
- Find P(E) and P(EC).
- Solution: P(E) = 2/6=1/3 and P(EC) = 4/6=2/3
- We can count the number of outcomes in E (there are 2) and the total number of outcomes in the sample space (there are 6). Similar for E complement.
Complement Rule for Probabilities
For an event E and the complement EC, the probability of EC is:
P(EC) = 1 – P(E).
We can represent and visualize the Complement Rule using the following Venn diagram:
Example: Complementary Probabilities
According to the American Kennel Club, 72% of American households own a dog. What is the probability that a randomly selected household does not own a dog?
Solution:
Conditional Probability
Suppose F and E and two different events. Then the notation P(F|E) is read “the probability of F given E.”
This probability is the probability that the event F occurs given that event E has already occurred.
Example: Conditional Probability
The table below describes the smoking habits of a group of asthma sufferers.
|
Gender |
Nonsmoker (N) |
Occasional Smoker (O) |
Regular Smoker (R) |
Heavy Smoker (H) |
Total |
|
Men (M) |
390 |
35 |
82 |
38 |
545 |
|
Women (W) |
400 |
36 |
108 |
35 |
579 |
|
Total |
790 |
71 |
190 |
73 |
1124 |
If one of the 1124 people is randomly selected, find the probability that the person is a nonsmoker given the person is a woman.
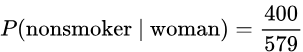
If one of the 1124 people is randomly selected, find the probability that the person is a woman given the person is a nonsmoker.
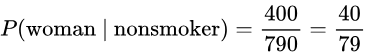
Attributions
- Content and structure adapted from RSCC Math 1410/1420 OER Team, 2022, CC BY 4.0.
