19 Addition Rule
Learning Objectives
- Determine whether events are mutually exclusive or not mutually exclusive
- Find probabilities using the Addition Rule
Mutually Exclusive vs Not Exclusive Events
Two events are mutually exclusive if they have no outcomes in common (or they cannot occur at the same time). Another name for mutually exclusive events is disjoint events.
Examples: Mutually Exclusive Events
For the following examples, determine whether the two events are mutually exclusive for a single trial.
- From a standard 52-card deck, drawing a red heart and a black spade.
- Solution: mutually exclusive. There are no cards that are BOTH hearts and spades.
2. From a standard 52-card deck, drawing a red heart and a queen.
- Solution: not mutually exclusive. There are cards that are hearts and queen- in particular, the queen of hearts!
Venn Diagrams
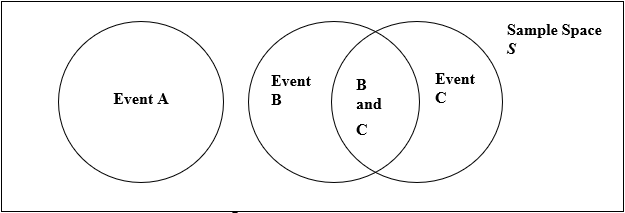
We often draw pictures of events using Venn diagrams. These pictures represent events as circles enclosed in a rectangle. The rectangle represents the Sample Space S, and each circle represents an event.
With Venn diagrams, you can determine if two events are mutually exclusive if they do not overlap. For example, in the image below, Events A and B are mutually exclusive, while Events B and C are not mutually exclusive.
Examples: Practice with Mutually Exclusive Events
- List all the outcomes for rolling a 6-sided die.
Solution: 1, 2, 3, 4, 5, 6
2. What would be the sample space for rolling a 6-sided die?
Solution: S = {1, 2, 3, 4, 5, 6}. The Sample space is the set of all possible outcomes.
3. Determine whether the events are mutually exclusive or not mutually exclusive.
- Event A – rolling an even number on 6-sided die
- Event B – rolling an odd number on 6-sided die
- Solution: mutually exclusive. There is no number that is BOTH even and ODD.
- Event A – rolling a number less than 3 on 6-sided die
- Event B – rolling an odd number on 6-sided die
- Solution: not mutually exclusive. There are odd numbers less than three, in particular, 1 is an odd number less than three.
Addition Rule
The addition rule, states, that for events E and F, the probability of E or F happening can be computed by adding the probabilities of E happening and F happening and then subtracting the probability of both E and F happening. In formula,
.
Note that if E and F are mutually exclusive, then P(E and F) = 0.
Examples of using the Addition Rule
Example 1.
Suppose that we have a bag of 10 marbles consisting of 4 red marbles, 3 blue marbles, and 3 yellow marbles.
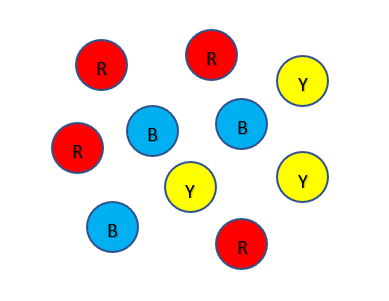
- What is the sample space for drawing a marble out the bag and recording the color?
- Solution: S = {red, blue, yellow}
- Are the events “drawing out a red marble” and “drawing out a blue marble” mutually exclusive? Why or why not?
- Solution: mutually exclusive because the marbles are solid colors. A marble can either be red OR blue but NOT both.
- If one marble is randomly selected from the bag, what is the probability of getting a red and blue marble?
- Solution: There are NO marbles that are both red and blue, so the probability of getting a red and blue marble is zero. This means
- If one marble is randomly selected from the bag, what is the probability of getting a red or blue marble?
- Solution: We can use the addition rule! The probability of getting a red marble is 4/10, the probability of getting a blue marble is 3/10, and the probability of getting a Blue and Red marble is 0. This mean:
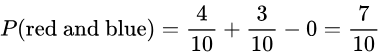
Example 2.
Use a 52-card deck to answer the questions below.
Source for picture (https://commons.wikimedia.org/wiki/File:Atlasnye_playing_cards_deck.svg)
- Are the events “drawing a queen card” and “drawing a heart card” mutually exclusive? Why or why not?
- Solution: not mutually exclusive because the queen of hearts is both
- If you pick a card at random from a well shuffled deck, what is the probability that you get a queen card and a heart?
- Solution: Since there is one card in the deck of 52 that is both a queen and heart, the probability is 1/52.
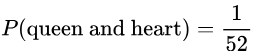
- If you pick a card at random from a well shuffled deck, what is the probability that you get a queen card or a heart?
- Solution: The probability of drawing a queen card is 4/25 (since there are four queens in the deck). The probability of drawing a hearts is 13/52 (since there are 13 hearts in the deck). Using the addition rule, we can compute the probability of getting a queen OR a heart:
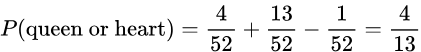
Example 3.
The table below describes the smoking habits of a group of asthma sufferers.
|
Gender |
Nonsmoker (N) |
Occasional Smoker (O) |
Regular Smoker (R) |
Heavy Smoker (H) |
Total |
|
Men (M) |
390 |
35 |
82 |
38 |
Enter total men |
|
Women (W) |
400 |
36 |
108 |
35 |
Enter total women |
|
Total |
Enter total nonsmokers |
Enter total occasional smokers |
Enter total regular smokers |
Enter total heavy smokers |
Enter total people |
- If one of the 1124 people is randomly selected, find the probability that the person is a nonsmoker and a woman.
- Solution: We see from the table of data that there are 40 0 women who are nonsmokers. This means:
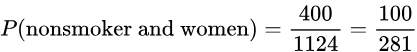
- If one of the 1124 people is randomly selected, find the probability that the person is a nonsmoker or a woman.
- Solution: Since there are 790 total nonsmokers and 579 total women, we can compute the probability of a nonsmoker OR women using the addition rule:
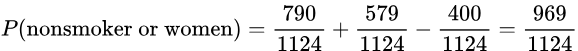
- If one of the 1124 people is randomly selected, find the probability that the person is an occasional smoker and a regular smoker.
- Solution: There is no one who is an occasional smoker and regular smoker- the type of smokers are all mutually exclusive, this means:
- If one of the 1124 people is randomly selected, find the probability that the person is an occasional smoker or a regular smoker.
- Solution: Using the addition rule, we can compute:
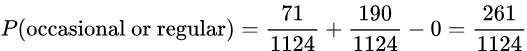
- If one of the 1124 people is randomly selected, find the probability that the person is a nonsmoker or a woman or a regular smoker. Would this probability be unusual?
- Solution: Again, using the addition rule:
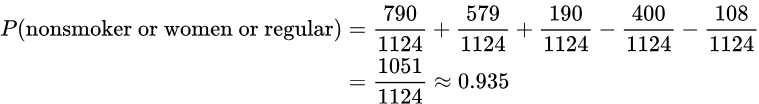
Attributions
- Content and structure adapted from RSCC Math 1410/1420 OER Team, 2022, CC BY 4.0.
- Image credits:
- Standard Deck Image: Дмитрий Фомин (Dmitry Fomin), CC0, via Wikimedia Commons
