"

5 Angles

Learning Objectives

  • Understand How to Draw and Name Angles
  • Understand Complimentary and Supplementary Angles
  • Describe Vertical and Interior Angles
  • Find the Sum of the Measures of the Interior Angles of a Convex Polygon with n Sides
  • Describe Angle Bisectors

Angles

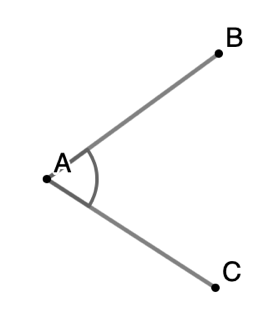
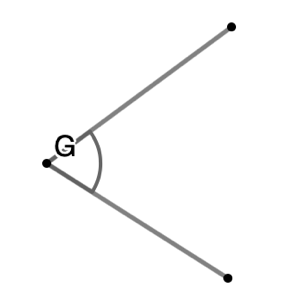
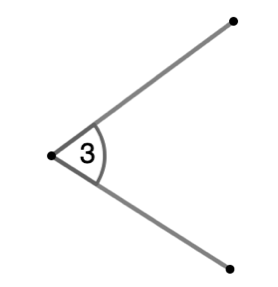
An angle is formed by two rays that have the same starting point, the vertex. Angles can be named in several ways:

  1. Using the vertex and a name (letter) from each arm.
  2. Using the vertex only.
  3. Using a number.

The symbol [latex]\angle[/latex] represents an angle, for example an angle named “A” is written as [latex]\angle A[/latex].

Examples

Below are pictures of angle followed by their conventional naming.

Angle BAC Angle BAC or angle CAB

Angle G Angle G

Angle 3 Angle 3

Special Angles

There are four types of special angles based on their measurements: right, acute, obtuse, and straight.

right angle: measures exactly 90 degrees.

acute angle: measures less than 90 degrees.

obtuse angle: measures more than 90 and less than 180 degrees.

straight angle: measures exactly 180 degrees.

Complementary and Supplementary Angles

Complementary angles are angle whose measures add up to 90 degrees.

They may be adjacent to each other or not. The total measure is what makes them complimentary.

Supplementary angles are angles whose measures add up to 180 degrees.

They may be adjacent to each other or not. The total measure is what makes them supplementary.

 

Examples

  1. Find the supplementary angles in this figure and name them correctly.

Two lines with one bisector.

Solution:

a and d, b and c, e and h, f and g, a and b, d and c, e and f, h and g

2.  Which of the following angles are complementary?

 

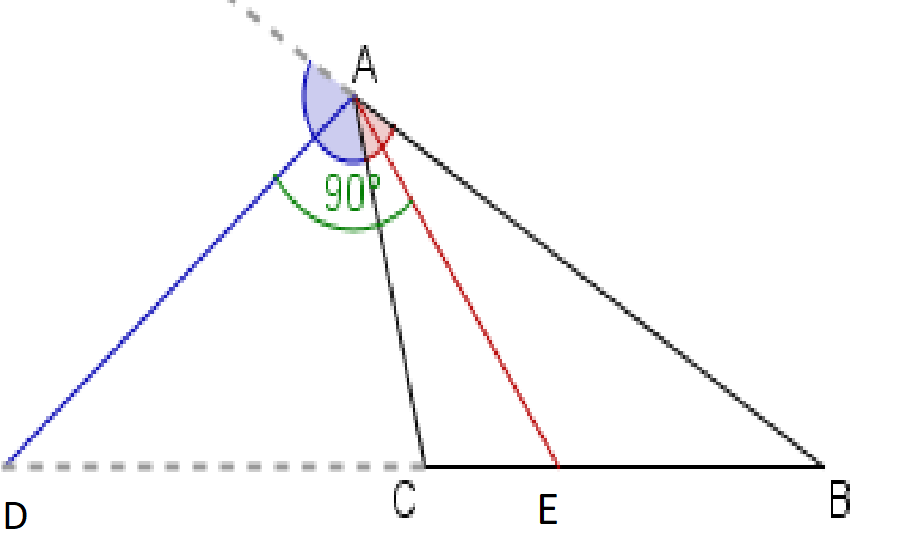
Triangle ABC with bisectors AE and AD.

Solution: Angle DAC + angle CAE = 90

 

Vertical and Interior Angles

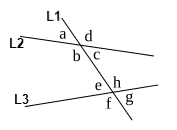
Vertical Angles are created when two lines intersect each other. In the figure, angles a and c, b and d, e and g, along with f and h make up the vertical angle pairs.

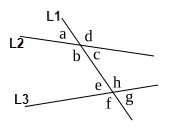
Two lines with a bisector

 

Interior Angles are formed one of two ways:

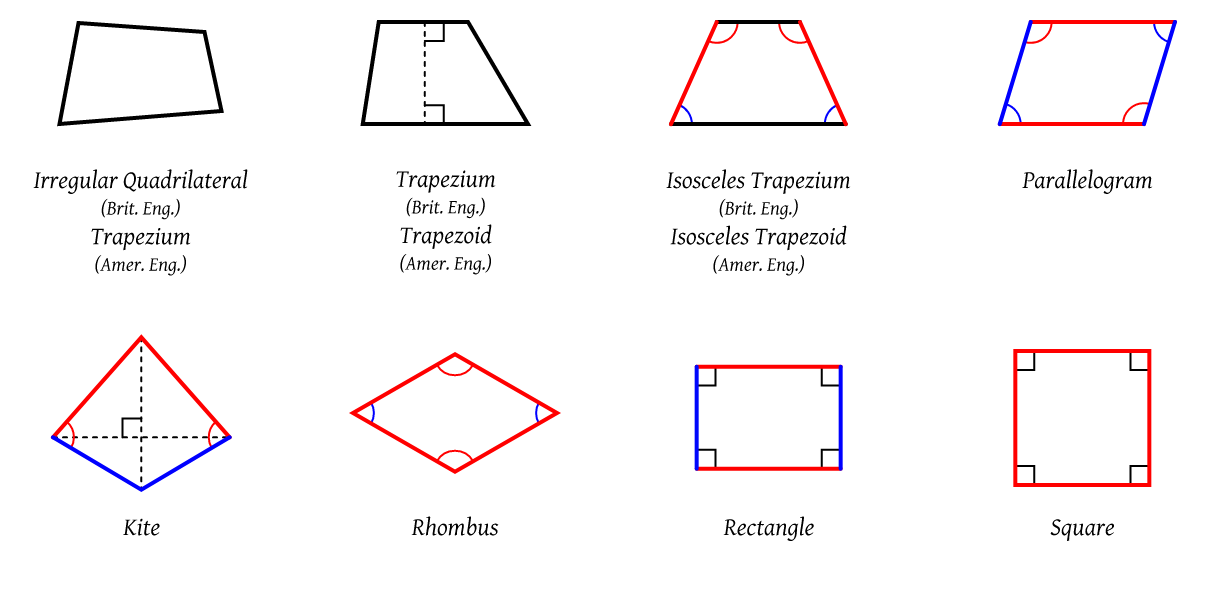
  1. The angles that lie inside a polygon as shown in these quadrilaterals.Examples of how interior angles are formed
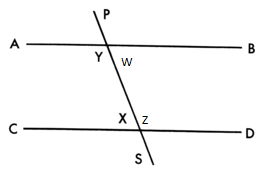
  2. The angles formed when a line, called a transversal, cuts through two parallel lines. The interior angles are the ones that lie in the area enclosed between the parallel lines. So, because lines AB̅ and CD̅ are given as parallel, the interior angles in this figure are W, X, Y and Z.

Two parallel lines and a bisector

 

Sum of the Measures of the Interior Angles of a Convex Polygon with n Sides

The sum of the measures of the interior angles of an n-sided polygon is given by the formula:

(n-2) x 180o

Thus, you only need to know the number of sides of the polygon to determine the total measure of the interior angles.

 

Examples

  1. Find the total interior angle measure of a 5-sided polygon.

Solution:(5-2) x 180 degrees = 3 x 180 degrees = 5402.      Find the total interior angle measure of a 23-sided polygon.

       Solution: (23-2) x 180 = 21 x 180 = 3780

 

Angle Bisectors

An angle bisector is a ray that divides an angle into two equal parts. In this figure, ∠AOB is bisected by ray OP.

Angle AOB with bisector OP

Examples

Name the angle bisector and the angles formed by the bisection.

Triangle ACB with angle bisector CD

Solution: Line CD and angle ACD with angle DCB

 

Attributions

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Mathematics for Elementary Education II Copyright © by Natalie Hobson is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book