11 Congruence, Similarity, and Symmetry
Learning Objectives
- Understand Congruent and Similar Figures
- Recognize Symmetric Figures
- Use valid notation for Congruency, Similarity and Symmetry
- Use Constructions to Show Congruency, Similarity and Symmetry.
Similarity
Similar objects have the same shape but not necessarily the same size. In other words, similar objects are scaled versions of one another.
One example of a similarity are squares. All squares have the same shape but sizes differ. Circles also are all similar. However, most geometric objects can have different shapes, all other quadrilaterals, triangles, and non-regular polygons are only similar if their shape is the same.
The symbol to show that two objects are similar is [latex]\sim[/latex]. In notations, the two squares below are similar can be written as
[latex]ABCD \sim EFGH.[/latex]
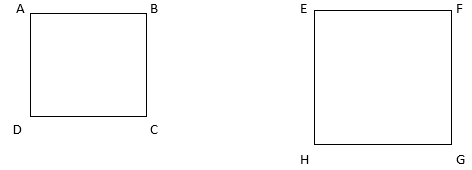
Note that the letters go in order around the figure, and they are in the same order, top left is the first letter, top right is the second, bottom right is the third and bottom left is the last letter in each name. This is the standard way to indicate labeling of figures.
Congruency
Congruent objects have the same shape and size. In other words, if you superimpose one object onto the other, the objects are congruent if all parts overlap exactly.
We use the symbol [latex]\cong[/latex] to notate when two objects are congruent. So, to describe congruence of the shapes below, we would write:
[latex]ABCD \cong EFGH[/latex].
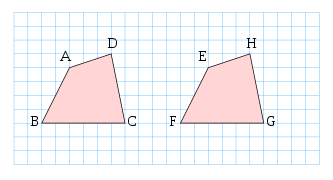
All congruent figures are also similar but not all similar figures are congruent (for example, the two squares above are similar but not congruent).
Symmetry
Symmetry in objects occurs if an operation or transformation maps the figure onto itself.
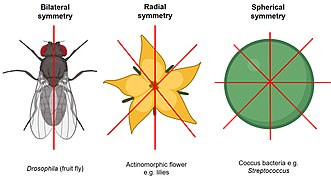
A circle rotated about its center has symmetry since no matter how much you rotate it, it will still show the same circle. But there is symmetry in many geometric figures. Three of the shapes in the left picture exhibit reflectional symmetry shown as dashed lines. Some types of natural symmetries are shown to the right. The two main types of symmetry are line (reflections) or turn (rotation) symmetry.
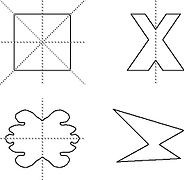
Line Symmetry
All the above symmetric figures have line symmetry since you can fold the page along any of the dashed or red lines and the images are mirrors of themselves. The square has multiple line symmetries as does the blob on the far left, the flower and the bacteria.
Turn Symmetry
Turn symmetry is where a figure can be rotated between 0 and 360 degrees to produce an identical image of itself. For example, in the image above, the square can be rotated 90, 180, or 270 degrees. The flower can be rotated either 30, 120, 210 or 300 degrees. And finally, the bacteria can be rotated any number of degrees!
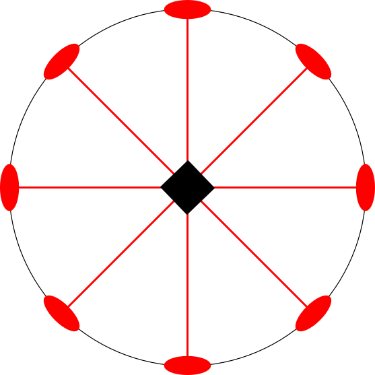
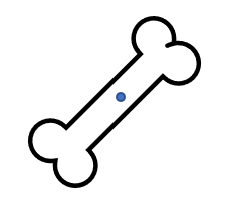
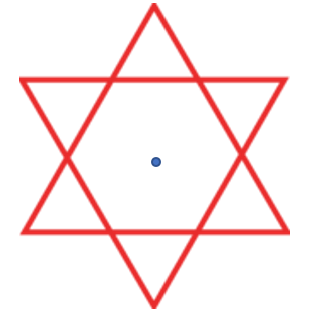
Point Symmetry
Any figure that has 180 degree turn symmetry also has point symmetry, where a point in the middle of the figure acts as the turn center of the figure. The circle is the perfect point symmetry example since you can rotate the circle about its center any number of degrees. But many figures have point symmetry as shown here. Using the marked center, you can rotate each of these around the point. Below are some examples.
Attributions
- Content and images, except where otherwise noted, adapted from "MATH 1420: Geometry Concepts for Teachers" by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 International License.
- Some pictures obtained from Wiki Commons
- Symmetry, Loggie, Public Domain.
- PG D'4, Bor75, CC BY-SA 3.0
- Congruence 4-gon, すじにくシチュー, CC0 1.0 Universal Public Domain Dedication.
- Construct Congruent Triangles, Joe Shanahan, Public Domain.
- Congruent Segments, Joe Shanahan, Public Domain.

