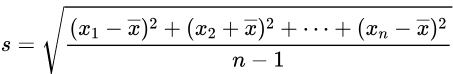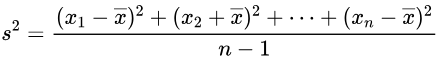25 Measures of Variance
Learning Objectives
This section deals with measuring the “variance” or spread of a set of data. When have you heard the word variance or spread before? Consider spreading jam or butter on toast…. you apply the jam and then move and spread the jam around on the toast…. similar in statistics “spread” (or variance) describes how the data is spread out or how the data varies. We measure the variance of a data set by calculating the range, standard deviation, or variance.
Find Range, Standard Deviation, and Variance by Hand
Measures of variance measures the spread of the data. Meaning is the data all very close to the center (or average) or are the a lot of very big values, very small values, or somewhere in between. Measures of spread deal with only quantitative (or numerical) data.
Range
To calculate the range of a set of data, we make the following computation:
Range = largest data value – smallest data value
Examples. Find the range of the following data set.
Note: we first need to sort the data from smallest to largest in order to find the largest and smallest data values.
Standard Deviation
The formula for sample standard deviation is given below.
In this formula [latex]x_1, x_2, ...., x_n[/latex] is your list of data values. n is the size of your data set (or the number of data values). [latex]\bar{x}[/latex] is the average or mean. See below for a detailed example of this computation.
Examples: Find the standard deviation for the sample data set.
Data set:
| 63 | 88 | 77 |
Solution:
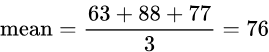
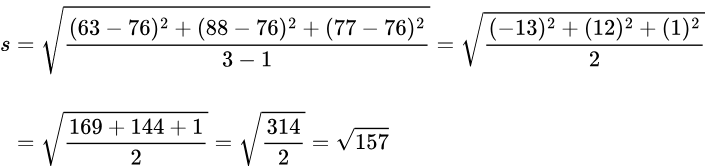
Variance
The formula for sample variance is given below.
The easy way to obtain the variance is to square the standard deviation. In other words, the standard deviation is the square root of the variance.
Examples: Compute the variance of the sample data below.
Data Set:
Solution: Since we already computed the standard deviation- we can square this value to compute the variance.
Attributions
- Content and structure adapted from RSCC Math 1410/1420 OER Team, 2022, CC BY 4.0.
