20 Multiplication Rule
Learning Objectives
- Determine whether events are independent or dependent
- Find probabilities using the Multiplication Rule
- Find probabilities using both the Multiplication Rule and Addition Rule.
Independent Events and Dependent Events
Two events A and B are independent if the knowledge that one occurred does not affect the chance the other occurs. If two events are NOT independent, then we say that they are dependent.
Examples: Independent vs Dependent Events
- Suppose you draw a card from a standard 52-card deck of cards and then roll a die. Are the events “draw a king” and “roll an odd number” independent or dependent? Explain.
Solution: independent
2. You randomly pick one donut from a box with 6 glazed, 3 jelly-filled, and 3 cream-filled donuts, and you eat the donut. Then you randomly pick a second donut from the box, and eat it. Are the events “picking a jelly-filled donut” and “picking a glazed donut” independent or dependent in this situation? Explain.
Solution: dependent
3. You randomly pick one donut from a box with 6 glazed, 3 jelly-filled, and 3 cream-filled donuts, and you put it back. Then you randomly pick a second donut from the box, and you put it back. Are the events “picking a jelly-filled donut” and “picking a glazed donut” independent or dependent in this situation? Explain.
Solution: independent
Replacement versus Without Replacement
When taking multiple samples (i.e., drawing a card multiple times)- we must consider wether we replace the object pulled before drawing a new object. If we take a sample and then replace- then each trial is independent. If we do not replace, then one trial depends on what we selected in the previous trial. This is summarized below:
Sampling with replacement: Selections are independent events.
Example 3 above demonstrates a with replacement situation- we put the doughnut back after selecting.
Sampling without replacement: Selections are dependent events.
Example 2 demonstrates a without replacement situation- we ate the chosen doughnut before selecting another.
Multiplication Rule
If we want to compute the probability of something happening that requires outcomes in a series of steps (see examples below), then the multiplication rule states that the probability of a certain sequence of outcomes happening is equal to the product of the probability of the outcome at each step. There is a slight consideration for calculating this probability for independent or dependent events- but this usually becomes clear in the context. This is summarized as a formula below.
Multiplication Rule:
If A and B are independent events then P(A then B) = P(A)* P(B).
If A and B are dependent events then P(A then B) = P(A)* P(B|A). That is, the probability that A happens times the probability that B happens (given A happened in the first step).
The multiplication rule becomes more clear though examples.
Multiplication Rule Example: Drawing Marbles.
Let’s Suppose that we have a bag of 20 marbles consisting of 8 red marbles, 5 blue marbles, and 7 yellow marbles. This is illustrated in the image below:
- What is the sample space for drawing two marbles out the bag and recording the color?
Solution: 
where B = blue, R= red, Y= yellow.
2. If 2 of the 20 marbles are randomly selected with replacement (meaning, one marble is drawn, the color is recorded, then put back in the bag), what is the probability of getting two red marbles?
Solution: P(both red with replacement) = 8/20 *8/20 = (8/20)^2 = 0.16. Notice that since the marble was replaced, the probability of drawing a red marble on the second draw is also 8/20- the same probability as drawing the red marble on the first draw.
3. If 2 of the 20 marbles are randomly selected without replacement, what is the probability of getting two red marbles?
Solution: P(both red without replacement) = 8/20 *7/19 = 0.14736842105. Notice that since the marble was not replaced, the probability of drawing a red marble on the second draw becomes 7/19- there are now only 19 total marbles, only 7 of them are red (the one drawn first- which is assumed to be red, is not replaced)
4. If 2 of the 20 marbles are randomly selected without replacement, what is the probability of getting a red and then a blue marble?
Solution: P(red then blue without replacement) = 8/20 *5/19 = 0.105. Notice that since the (red) marble was not replaced, the probability of drawing a blue marble on the second draw becomes 5/19- there are now only 19 total marbles, 5 of which are still blue.
5. If 2 of the 20 marbles are randomly selected without replacement, what is the probability of getting a red and a blue marble, in any order?
Solution: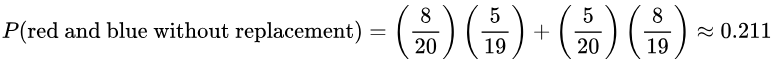 
6. If 2 of the 20 marbles are randomly selected with replacement, what is the probability of getting a red and then a blue marble?
Solution: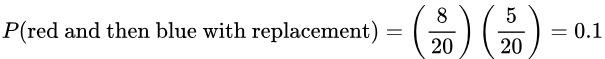 
7. If 2 of the 20 marbles are randomly selected with replacement, what is the probability of getting a red and a blue marble, in any order?
We conclude this chapter with two more example situations.
Multiplication Rule Example: Light Bulbs
A bin contains 60 light bulbs, of which 10 are defective. Consider the following scenarios.
- If 4 light bulbs are randomly selected from the bin with replacement, find the probability that all the bulbs selected are good ones.
Solution: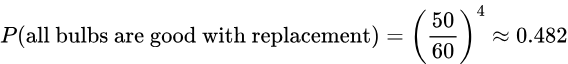 
2. If 4 light bulbs are randomly selected from the bin without replacement, find the probability that all the bulbs selected are good ones.
Solution: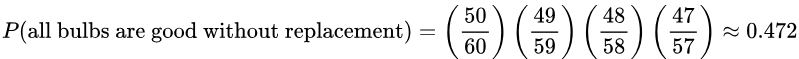 
3. If 4 light bulbs are randomly selected from the bin without replacement, find the probability that the first bulb was good, the second bulb was defective, the third bulb was defective, and the fourth bulb was good. Let’s appreciate this sequence of events as GDDG.
Solution: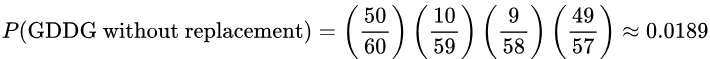 
4. If 4 light bulbs are randomly selected from the bin with replacement, find the probability that the first bulb was good, the second bulb was defective, the third bulb was defective, and the fourth bulb was good.
Solution: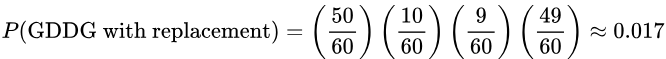 
5. If 2 light bulbs are randomly selected from the bin with replacement, find the probability that exactly one of the bulbs is good.
Solution: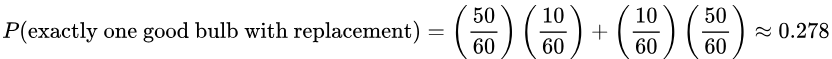
6. If 2 light bulbs are randomly selected from the bin without replacement, find the probability that exactly one of the bulbs is good.
Solution: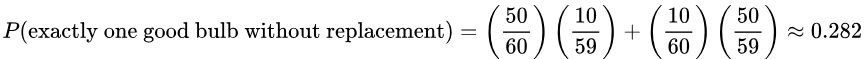 
Notice how this solution also uses the addition rule!
Multiplication Rule Example: Selecting people
The table below describes the smoking habits of a group of asthma sufferers.
|
Gender |
Nonsmoker (N) |
Occasional Smoker (O) |
Regular Smoker (R) |
Heavy Smoker (H) |
Total |
|
Men (M) |
390 |
35 |
82 |
38 |
545 |
|
Women (W) |
400 |
36 |
108 |
35 |
579 |
|
Total |
790 |
71 |
190 |
73 |
1124 |
- If two people are randomly selected without replacement from the 1124 subjects, find the probability that they are both heavy smokers.
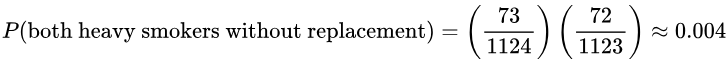
- If two people are randomly selected with replacement, find the probability that they are both women.
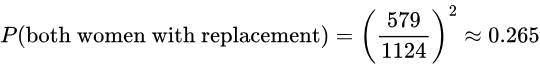
- If four people are randomly selected with replacement, find the probability that they are all women.
- If two people are randomly selected with replacement, find the probability that the first person is a man and the second person is a woman. Would this probability be unusual?
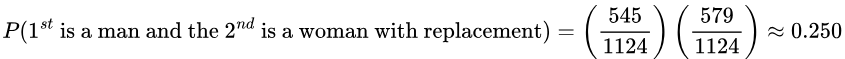
- If two people are randomly selected without replacement, find the probability that the first person is a nonsmoker and the second person is an occasional smoker. Would this probability be unusual?
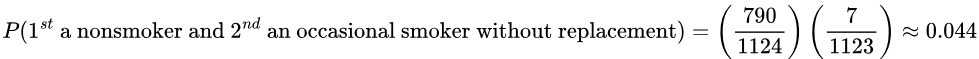
Attributions
- Content and images adapted from “MATH 1420: Geometry Concepts for Teachers” by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 International License.
- Independent and mutually exclusive materials based on the content in Openstax ‘Introductory Statistics’
