4 Preliminary Geometric Objects: Points, Lines, and Planes
Learning Objectives
- Define and name points, lines, rays, planes, and angles
- Determine if points are collinear or coplanar
- Identify intersections of lines with lines, lines with planes, and planes with planes
Define and Name Points, Lines, Rays, Planes, and Angles
Points
A point is a location. A point is zero-dimensional which means that it has no length, depth, or width. We represent points with a dot and name them using letters.
Lines
A line is a collection of an infinite number of points extending in both directions. A line is one-dimensional which means it has infinite length, but no thickness or depth. Lines are named using upper case letters with a line over the top or with a single lower case letter.
Examples: Name the following lines.

Solution: [latex]\bar{DE}[/latex]

Solution: p
Rays
A ray is a collection of an infinite number of points extending in one direction from a point, the endpoint. Rays are named using upper case letters with an arrow over the top in the direction of the ray. The first letter in the name of a ray is always the endpoint.
Example: Name the following ray.
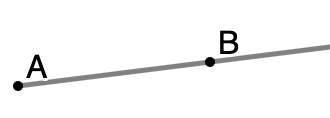
Solution: ![]()
Planes
A plane is a two-dimensional surface that extends infinitely far. A plane has length and width, but not depth. You can think of a plane as an infinite piece of paper. Planes are named by either a single letter or by three letters that do not all lie on the same line. (Points that lie on the same line are called "colinear".)
Examples: Name the following planes.
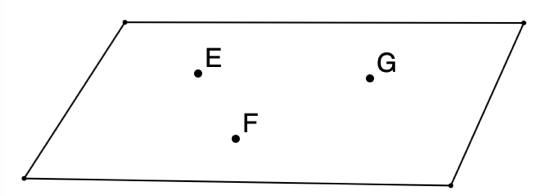
Solution: EFG
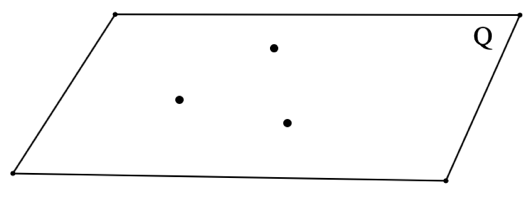
Solution: Q
Angles
An angle is formed of two rays that have the same starting point, the vertex. Angles can be named in several ways:
- Using the vertex letter and a letter name from each arm
- Using the vertex letter only
- Using a number
More details about angles will be discussed in the next section.
Examples: Name the following angles.
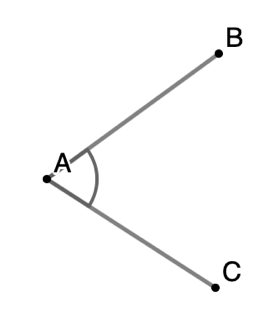
Solution: [latex]\angle CAB[/latex]
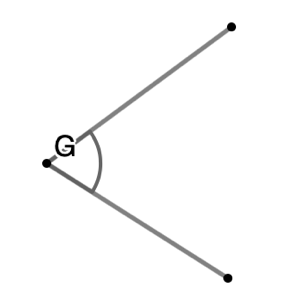
Solution: [latex]\angle G[/latex]
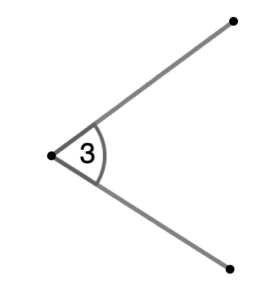
Solution: [latex]\angle 3[/latex]
Measuring Angles
Angles are typically measured using an degrees or radians. It was the ancient Babylonians that devised the method for measuring angles by dividing a circle into 360 equal parts, called degrees. Radians are also used to measure circles, one radian around a circle is the length of one radius around a circle. This means that an entire circle measures [latex]2 \pi[/latex] radians. More discussion on [latex]\pi[/latex] will take place in our section on circles. For now, we will stick to using degrees to measure angles.
The tool to measure angles in degrees is called a protractor. Degrees can be broken down even further. There are 60 minutes in one degree and 60 seconds in one minutes. To use a protractor one ray of the angle sits on the end of the protractor (at 0 degrees) and the other ray will then extend to the degree measurement of that angle. See the demonstration below.
Types of Angles
There are four types of angles based on their angle measurements. These are right angles, acute angles, obtuse angles and straight angles.
Right angles measures exactly 90°.
Acute angles measure less than 90°
Obtuse angles measure greater than 90°.
Straight angles measures 180° and consists of two rays that are going in exactly opposite directions from a common vertex.
Determine If Points are Collinear and Coplanar
Collinear Points
When two or more points lie on a straight line, then the points are collinear. When points lie in the same plane, they are said to be coplanar.
Examples: State which points are collinear and which are coplanar.
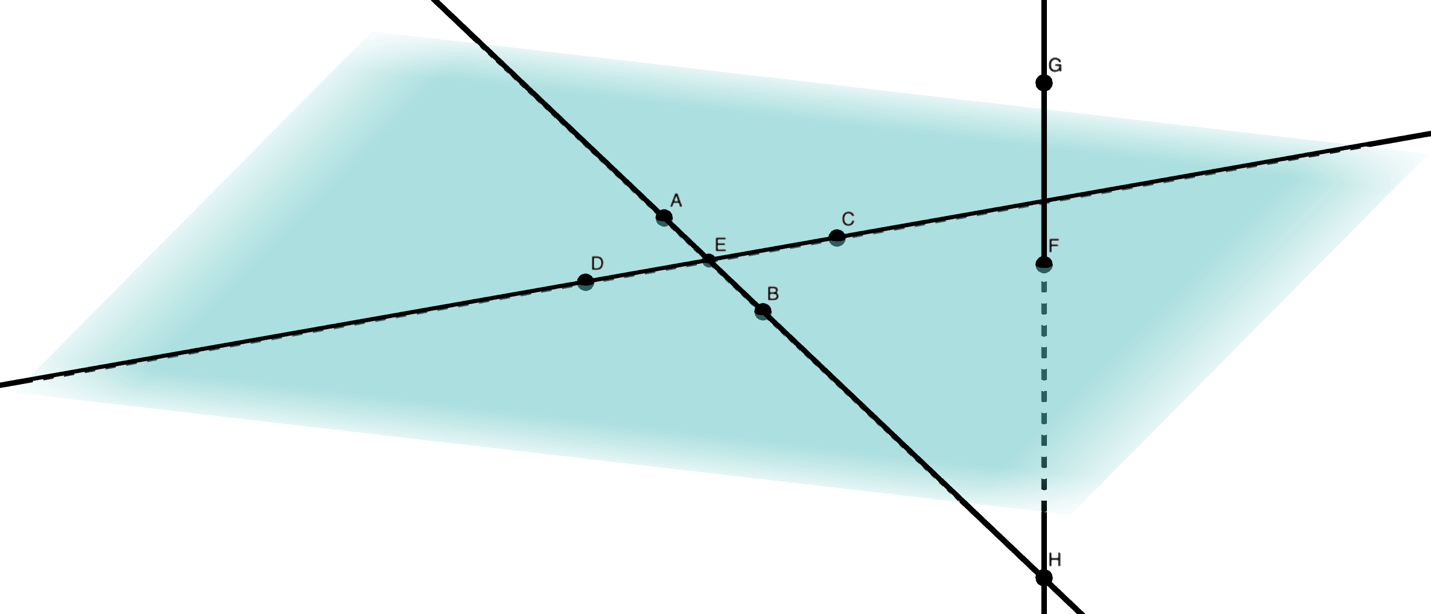
Solution: Collinear points A, E, B; points D, E, C; points G, F, H. Coplanar: points A, B, C, D, E, H; points A, E, B, H, F, and G. Notes: any TWO lines form a plane. Think about why that is.
Identify Intersections
Intersection of a Line with a Line
The intersection of two lines is a point.
Intersection of a Line with a Plane
The intersection of a line that does not lie on a plane and the plane is a point.
Intersection of a Plane with a Plane
The intersection of two unique planes (or two flat surfaces) is a line.
Examples: Find the intersections
Examples: Find the intersections.
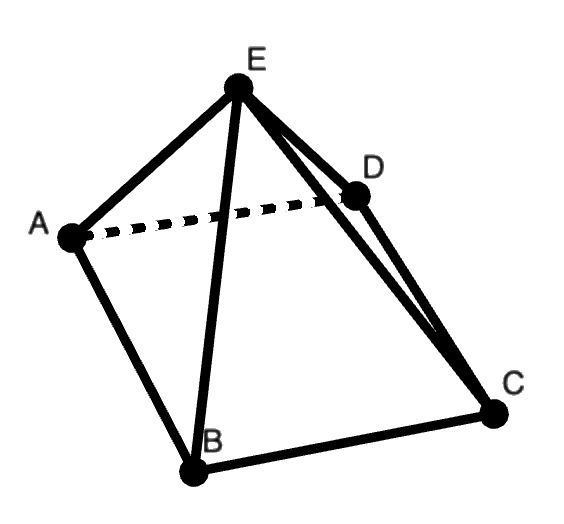
- Find the intersection of side AEB and side EBC.
Solution: This is line EB.
2. Find the intersection of [latex]\overline{AD}[/latex] and [latex]\overline{CD}[/latex].
Solution: This is point D.
3. Find the intersection of side AED and [latex]\overline{EB}[/latex]
Solution: This is point E.
Parallel and Perpendicular Lines
Parallel lines are lines that never meet in a plane. The notation to indicate that two named lines are parallel is [latex]m || n.[/latex]
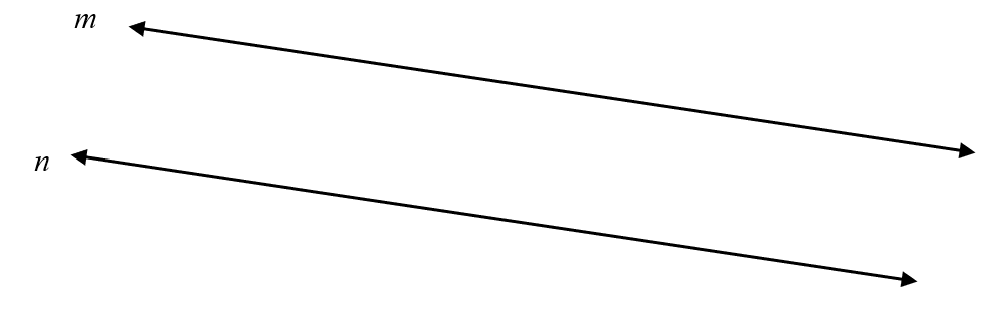
Perpendicular lines are lines that meet at a right angle. The notation to indicate that two lines are perpendicular is [latex]m \perp n.[/latex]
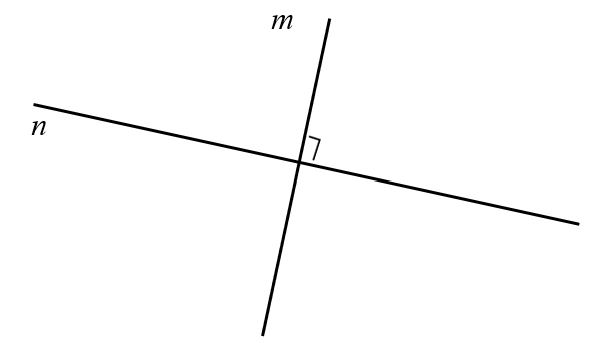
Example: Identify the parallel and perpendicular lines in the figure below.
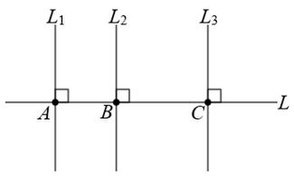
Lines L1, L2, and L3 are all parallel to each other. Each of these lines are perpendicular to line L. This is also a theorem. Two lines that are perpendicular to the same line are parallel.
Attributions
- Content and images, except where otherwise noted, adapted from "MATH 1420: Geometry Concepts for Teachers" by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 Internantial License.
- Other images:
- "Protractor measure small va.gif" by Lfahlberg, Wikimedia Commons, CC BY-SA 3.0, https://commons.wikimedia.org/wiki/File:Protractor_measure_small_va.gif.


