10 Quadrilaterals
Learning Objectives
- Understand quadrilaterals
- Recognize the difference between quadrilaterals
Quadrilaterals
A quadrilateral is a four-sided figure made up of straight lines. Quadrilaterals are a special type of polygon. A polygon is a shape made of straight line segments (for example, triangles are also polygons).
Below is an image of some common types of quadrilaterals.
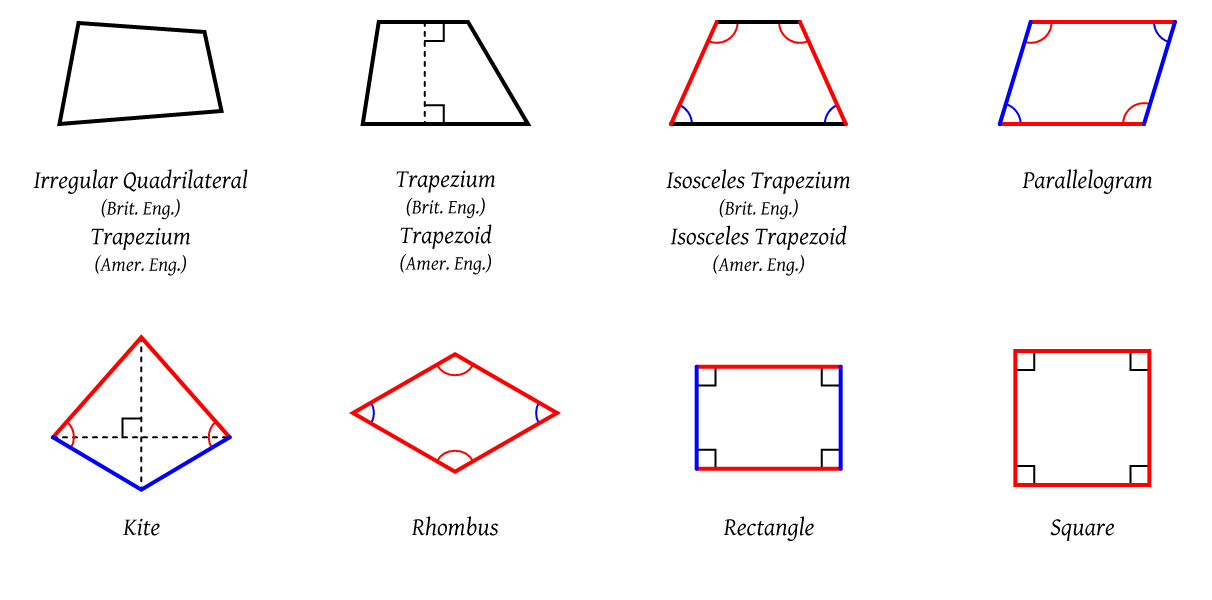
Below is an explanation of some special types of quadrilaterals.
- A trapezoid is a quadrilateral that has exactly one pair of parallel sides.
- An Isosceles trapezoid is a trapezoid that has congruent base angles (see pictures- red and blue curves) which make non-parallel sides of equal length (see red sides).
- A kite is a quadrilateral that has two sets of adjacent sides that are the same length.
- A parallelogram has two sets of parallel sides. In the diagram, above the two red sides are equal and parallel, and the two blue sides are equal and parallel.
- A rhombus is a quadrilateral that has all four sides of equal length.
- A rectangle is a quadrilateral that has four right angles.
- A square is a quadrilateral that has four equal sides and four right angles.
From the definitions of some special quadrilaterals above, we have the following relationships: The rhombus, the rectangle and square are all parallelograms as they also have opposite sides that are equal and parallel. A square is also a rhombus as it has four equal sides. And the square is also a rectangle as it has four right angles.
Properties of Quadrilaterals:
The special quadrilaterals above have some properties that follow from their definitions. These properties are:
- A trapezoid has consecutive angles between parallel sides that are supplementary.
- In an isosceles trapezoid, each pair of base angles are congruent, and pairs of opposite sides are congruent. If a trapezoid has congruent base angles, it is isosceles.
- A parallelogram is a trapezoid that has opposite sides that are parallel. Opposite angles are also congruent, and each pair of consecutive angels are supplementary. The diagonals of a parallelogram bisect each other.
- A rectangle has all of the previous properties, plus all the angles are right angles. Diagonals of a rectangle also bisect each other.
- A kite has diagonals that are perpendicular and one of the diagonals bisects the other and one pair of nonconsecutive angles.
- A rhombus has all the properties of the parallelogram and the kite. The diagonals of a rhombus are congruent to and bisect each other. Each diagonal bisects opposite angles.
- A square has all of the properties of the parallelogram, the rectangle and the rhombus.
Quadrilaterals and their Symmetries
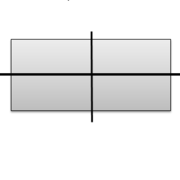
A rectangle can have symmetry if lines are drawn which bisect (cut in half) the parallel sides of the rectangle.
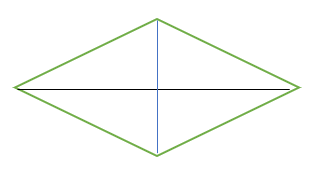
A rhombus can have symmetry if you connect opposite angles, that is use the diagonals. The kite is similar.
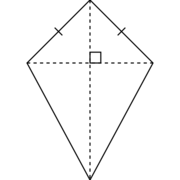
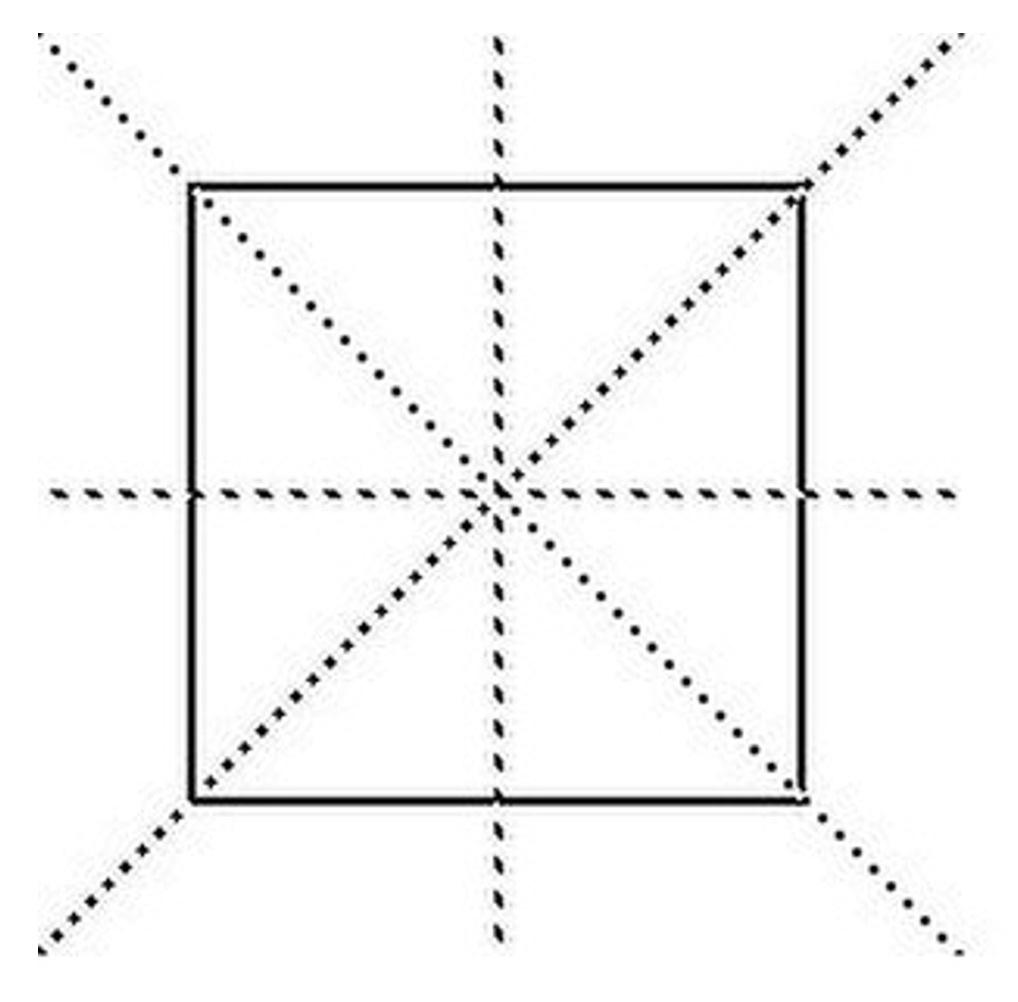
Since a square is both a rectangle and a rhombus, its symmetries are both.
Attributions
- Content and structure adapted from RSCC Math 1410/1420 OER Team, 2022, CC BY 4.0.
- Some of the diagrams used are from Wiki Commons,
- https://commons.wikimedia.org/wiki/File:Quadrilaterals.svg
- https://upload.wikimedia.org/wikipedia/commons/thumb/8/87/Twee_simmetrielyne.png/640px-Twee_simmetrielyne.png
- https://commons.wikimedia.org/wiki/File:Wongvarit_kite.png
