6 Simple Curves and Surfaces
Learning Objectives
- Understand simple curves
- Recognize simple closed surfaces
- Recognize and identify polygons
- Recognize and identify regular polygons
- Recognize simple closed surfaces
- Recognize and identify polyhedra and regular polyhedra
Simple Curves
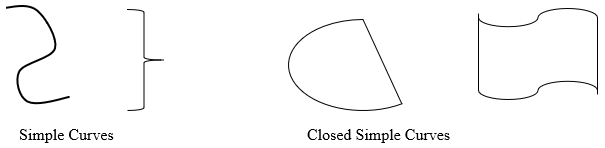
A simple curve is a curve that does not cross itself. A closed simple curve has the same start and stopping point.
Examples of simple curves:
Polygons are closed curves whose sides are all made up of lines.
Examples of Polygons:
Note: All polygons are simple, closed curves, but they also have all sides lines (not curves).
Examples
Determine if the following are simple curves, closed simple curves, or polygons:
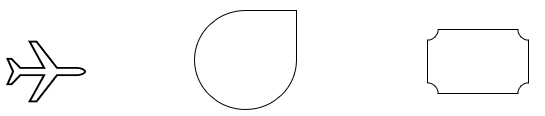
Solution: All of the above shapes are closed simple curves and not polygons
Solution: In order, these objects are a polygon, simple curve (not closed), polygon.
Regular polygons are polygons in which the interior angles all have the same measure and all side lengths are equal. This means they are equilateral (equal side lengths) and equiangular (equal angles).
Examples
Examples of regular polygons include equilateral triangle (three sides of the same length) and squares.
Below are images of a regular pentagon and a regular hexagon.
.
These are not the only regular figures, however, but the most common you will see in your classroom.
Simple Closed Surfaces
A simple closed surface has exactly one interior, has no holes, and is hollow. It has an interior, a surface, and an exterior. For example, a can of soup, a cereal box, an inflatable inner tube, or a beach ball are all simple, closed surfaces.
The set of all points on a simple closed surface along with all its interior points is called a soli.
A polyhedron (plural is polyhedra) is a simple closed surface with all the faces made up of polygonal regions. The cereal box is a polyhedron, but the soup can is not. A face is any of the polygonal regions making up the polyhedron. The points where two faces come together are called edges. The points where two or more edges come together are called vertices (or vertex if singular point).
Surfaces that are not polyhedra include spheres, cones, cylinders, and any solid with a curved surface.
Examples
Below are some images of polyhedra. Other examples of polyhedrons include prisms, pyramids, boxes, etc.
A regular polyhedron is one whose faces are identical regular polygonal regions such that the number of edges that meet at each vertex is the same for all the vertices of the polyhedron. There are five regular polyhedral as shown below.
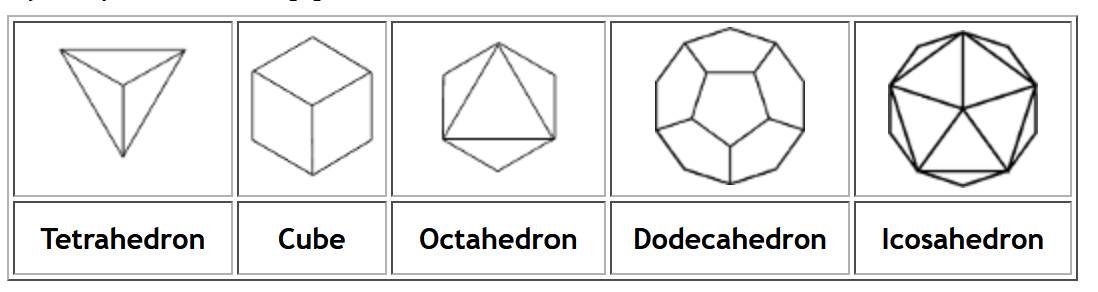
Examples
These D&D dice are regular polyhedra.
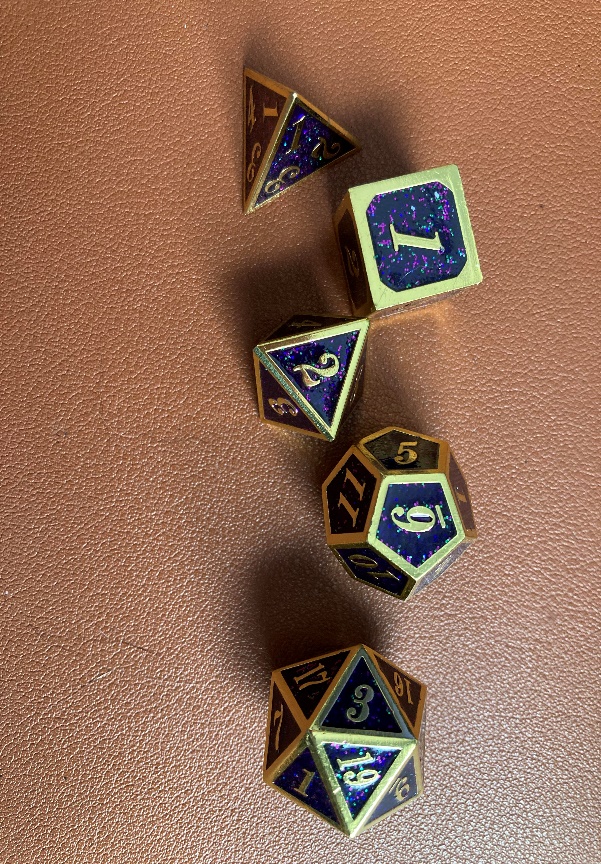
Examples: Decide if the following solids are polyhedra or not.
a.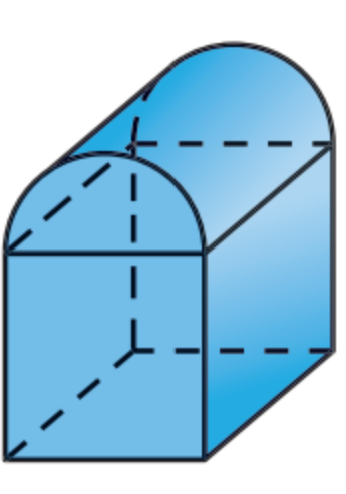 
. b. 
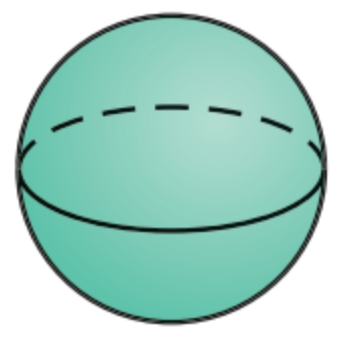c.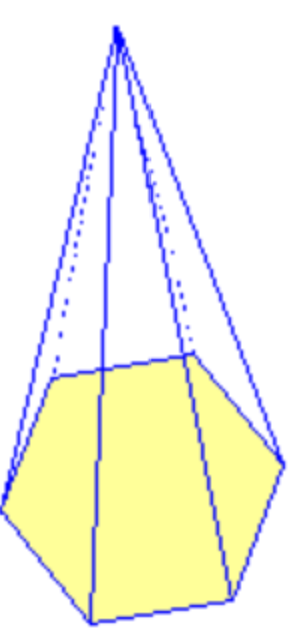 
Solution:
a) No: curves on surface- not all polygon sides.
b) No, curves for entire surface.
c) Yes, all sides are polygons.
d.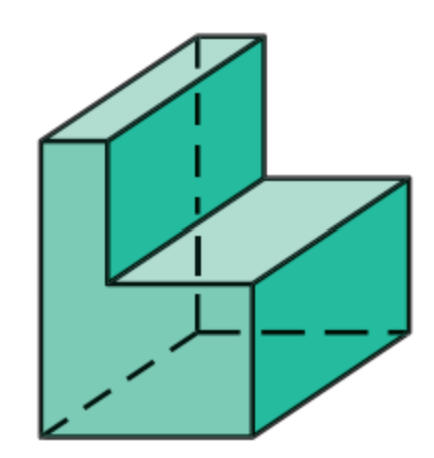 
. e. 
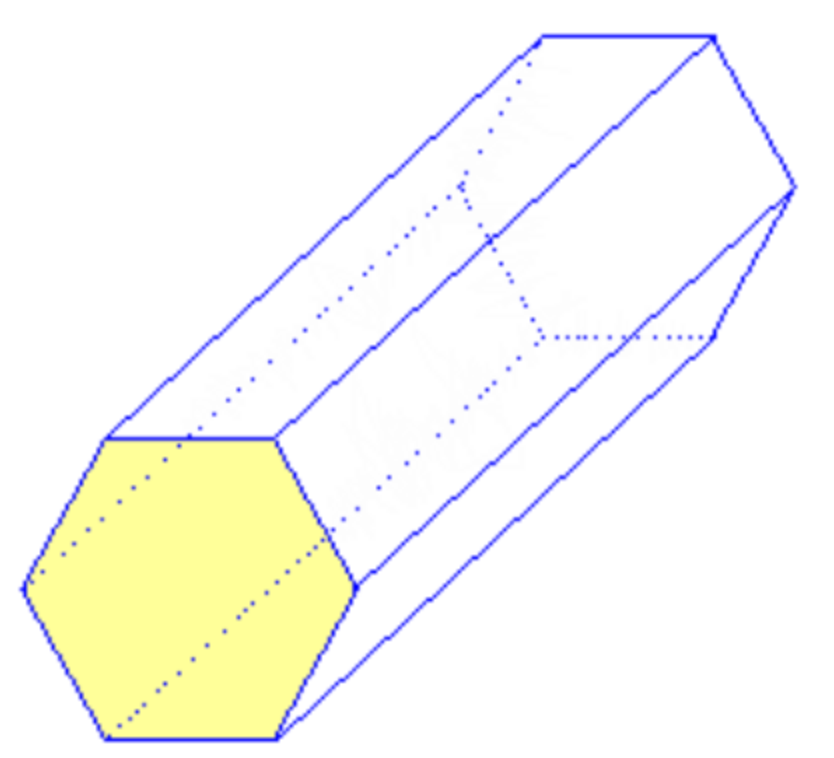. f.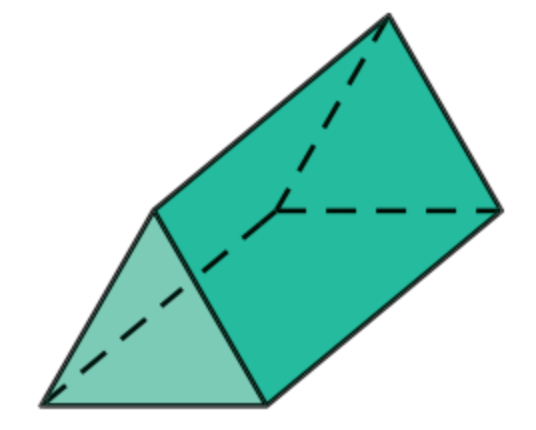
Solutions:
d, e, f: Yes, all of sides of all figures are polygons.
Attributions
- Content and images, except where otherwise noted, adapted from “MATH 1420: Geometry Concepts for Teachers” by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 International License.
- Some images used from Wiki Commons,
- Pentagon, image by Marko Cavara, Wikimedia Commons, CC BY-SA 4.0.
- Old South African Stop Sign, image by RedaCECThis, Wikimedia Commons, Public Domain.
- Some Regular Polyhedrons, image by A2569875, Wikimedia Commons, CC BY-SA 4.0.
