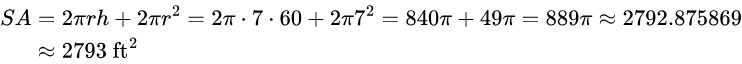15 Surface Area
Learning Objectives
Objectives:
- Determine the formulas for the surface area of common solid figures
- Find the surface area of solid figures
Find the Surface Area of Solids
The surface area of a solid is area that all the surfaces of the solid occupy.
Examples: Determine the formulas for the surface area of the following common figures.
Solution:
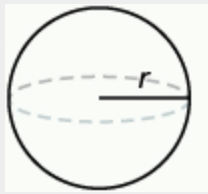
Sphere: [latex]SA = 4 \pi r^2[/latex]
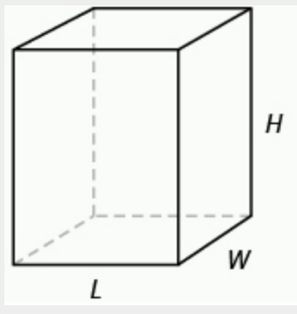
Rectangular Prism: SA = 2 ( LW + WH + LH)
Solution:
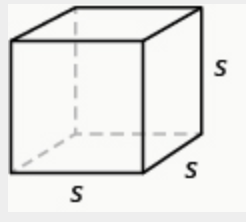
Cube: [latex]SA = 6s^2[/latex]
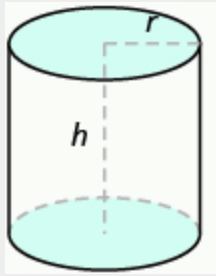
Cylinder: [latex]SA = 2 \pi r^2 + 2 \pi r h[/latex]
**Similar to area formulas- you should not necessarily just memorize the SA formulas of basic shares. You should understand that SA is made by adding up the areas of each side of the solid shape.
The following examples demonstrate some real-world surface area applications.
Examples: Find the indicated surface area.
A cylindrical jam jar has a radius of 2.5 inches and a height of 5 inches. What is the surface area of the jar? Round to two decimal places at the end.
Solution:
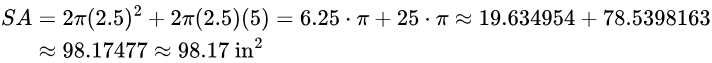
2.
The Earth is not perfectly spherical, but we will assume it is for this problem. The diameter of Earth is approximately 12,756 kilometers. What is the surface area of Earth in kilometers squared and miles squared? Hint: There are 0.621 miles in one kilometer.
Solution:
Now the radius is half of the diameter, so the radius of the earth is approximately 6378 kilometers. This leads to the following computation.
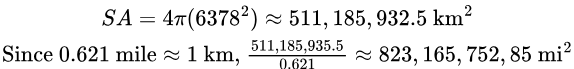
3.
There are two toy boxes in the nursery. One box is 3 feet long, 2 feet tall, and 1.5 feet wide. The other box is 2.5 feet long, 4 feet wide, and 1 foot tall. Which box has a larger surface area?
Solution:
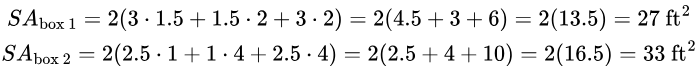
So the second box has a larger surface area.
The surface area of a pyramid is the sum of the lateral surface area and the area of the base. A right regular pyramid is a pyramid such that the surface sections connecting the tip to each vertex of the base are congruent and the base is a regular polygon.
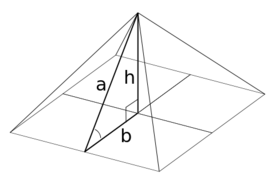

Use the above information is used to help compute the solution in the following example.
Examples
Find the surface area of the right regular pyramid above if b = 5 and a = 6. Note that b in the figure is only half the length of the base.
Solution:
Since b = 5, the length of each aside is 2 • 5 = 10 and P = 4 • 10 = 40. B is the area of the base which is [latex]10^2 = 100[/latex].
SA = [latex]\frac{1}{2} (10) \cdot 6 + 100 = 30 + 100 = 130[/latex]
- To find the surface area of irregular figures, we can divide the given figure into shapes that we can find the surface area of and add those values together to get the entire surface area. Be sure to recognize two sides of individual solids that the together as are not part of the surface area.
Similar to computing areas- we sometimes need to break up an object into parts and compute surface area of each part. This is done in the following Example.
Examples
Some formulas for shapes with curved sides (such as cones or shperes) are okay to be memorized or looked up. To determine these formulas it is required to use methods of calculus or more detailed numerical analysis.
Examples
Find the surface area of the right circular cone shown, using the formula
Use the radius 12 cm and the slant height, L, of 18 cm.
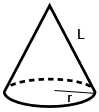
Solution:![]()
Attributions
- Content and images, except where otherwise noted, adapted from "MATH 1420: Geometry Concepts for Teachers" by the RSCC Math 1410/1420 OER Team under Creative Commons Attributions 4.0 International License.
- Some portions of this content adapted from Lumen Learning, Developmental Math Emporium, Module 8: Geometry. Data derived from NASA, The Cosmic Distance Scale: Earth Information. Public Domain.
- “Mathematical Pyramid.” Wikimedia Commons, uploaded by user Valepert, 21 September 2006, https://commons.wikimedia.org/wiki/File:Mathematical_Pyramid.svg. Released into the public domain by the copyright holder.