4 Conversion Factors for Changing Recipe Yields
Instructions for Changing Recipe Yields
While proportions can be very helpful for adjusting a recipe, there is a shortcut that makes the process go faster, and that is using a conversion factor. A conversion factor is a ratio that is converted to a decimal number and then used to change the amount of each ingredient in proportion. Here is how you find the conversion factor:
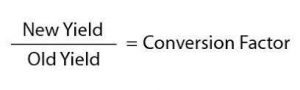
If you have a recipe that yields four dozen, or 48, cookies, and you want to make five dozen, or 60, cookies, you would find the conversion factor like this: Your conversion factor is 1.25, so you would simply take every ingredient amount and multiply it by 1.25 for your new recipe.
If you have fractions in your recipe, you can convert the decimal number to a fraction so you can use a calculator to adjust the recipe. Here is a link that will convert a decimal to a fraction: Decimal to Fraction You may use it for assignments and quizzes in this course. In the above case, the conversion factor of 1.25 converts to .
It’s also helpful to memorize how some common fractions are expressed as decimals:
| 1/8 | 0.125 |
| 1/4 | 0.25 |
| 1/3 | 033* |
| 3/8 | 0.375 |
| 1/2 | 0.5 |
| 5/8 | 0.625 |
| 2/3 | 0.67* |
| 3/4 | 0.75 |
| 7/8 | 0.875 |
*Not exact. Rounded to nearest hundredth.
Let’s try this with a recipe for salad dressing:
3 tablespoons olive oil
teaspoon garlic powder
1 tablespoon red wine vinegar
1 teaspoon Dijon mustard
teaspoon salt
teaspoon black pepper
1 teaspoon honey
1 teaspoon dried basil
This recipe yields cup. But let’s say you want to make more for a much bigger salad. Instead of
cup, you would like to make
cups. To find the conversion factor, you would divide the new yield by the old yield:
Your conversion factor is 4.5, although if you want to use a fraction calculator to make the adjustments, you will find it easier to use .
Now we will multiply each ingredient amount by 4.5, or :
3 tablespoons olive oil tablespoons olive oil
teaspoon garlic powder
teaspoons garlic powder
1 tablespoon red wine vinegar tablespoons red wine vinegar
1 teaspoon Dijon mustard teaspoons Dijon mustard
teaspoon salt
teaspoons salt
teaspoon black pepper
teaspoons black pepper
1 teaspoon honey teaspoons honey
1 teaspoon dried basil teaspoons dried basil
Assignment
Purpose
To practice changing recipe yields using the conversion factor.
Outcomes
By completing this assignment, you will be able to…
- Calculate the conversion factor to adjust a recipe yield.
- Use the conversion factor to adjust the ingredients in a recipe.
Instructions
To complete this assignment…
- Look at the recipes you are given.
- Calculate the conversion factors based on the changes in yield you are given.
- Change the amounts to use for each ingredient in the recipe.
Tips for Success
To help in the completion of this assignment, make sure to:
- Look carefully at the change in yield so you can calculate the correct conversion factor.
- Understand that if an ingredient amount is given as a fraction, the new ingredient amount should also be given as a fraction.
Changing Recipe Yields Assignment
This recipe for cookies yields 24. Adjust the recipe so that that it will yield 12.
1 cup butter, softened
cup white sugar
1 cups packed brown sugar
2 eggs
1 teaspoon vanilla extract
2 cups all-purpose flour
1 teaspoon baking powder
1 teaspoon salt
1 teaspoons ground cinnamon
3 cups quick cooking oats
This recipe for chicken wing sauce yields enough for 50 chicken wings. Adjust the recipe so it will yield enough for 125 chicken wings.
cup honey
4 tablespoons soy sauce
4 large garlic cloves crushed
1 tablespoon fresh ginger finely diced
teaspoon chili powder
teaspoon cinnamon
teaspoon cloves
cup water
1 teaspoon corn starch
This recipe for sauted green beans yields 5 cups. Adjust the recipe so it will yield cups.
2 tablespoons olive oil
teaspoon red pepper flakes
teaspoon dried cilantro
1 pounds green beans, trimmed
2 cloves garlic, minced
teaspoon salt
2 tablespoons water

