Multiplying fractions
In the following, “A/B” represents the fraction “A over B.” For example, “2/3” refers to the fraction “2 over 3” or “two-thirds.” In the fraction, A/B, “A” is called the numerator and “B” is called the denominator.
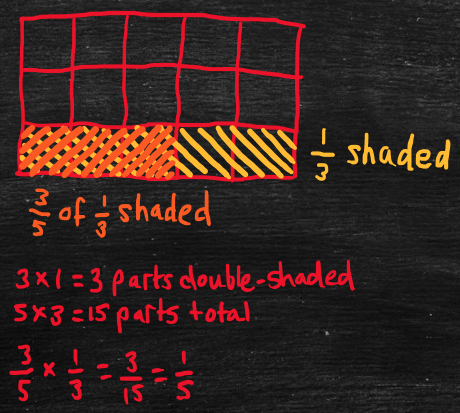
To multiply two fractions together, multiply the numerators and the denominators separately, then simplify if necessary. For example,
- 3/5 x 1/3 (three-fifths times one-third).
- First, multiply the numerators: 3 x 1 = 3.
- Next, multiply the denominators: 5 x 3 = 15.
- Finally, simplify: 3/15 is equivalent to 1/5 (see 1.3: Simplifying fractions).
- This works because “3/5 x 1/3” represents “three-fifths of one-third.”
- Divide a unit rectangle into thirds (horizontally) and shade one-third.
- Divide the rectangle into fifths (vertically) and double-shade three-fifths of the shaded one-third.
- The number of double-shaded parts is 3 x 1 = 3 (the product of the numerators).
- The total number of parts is 5 x 3 = 15 (the product of the denominators).
- The answer is the number of double-shaded parts (3) divided by the total number of parts (15), i.e., 3/15, which simplifies to 1/5.
The video below works through some examples of multiplying fractions.
Video Tips
Practice Exercises
Do the following exercises to practice multiplying fractions.
Attribution
This chapter adapted from Pardoe, I. (2023). Mathematics for Elementary Teachers. Thompson Rivers University Open Learning. https://mathforteachers.pressbooks.tru.ca/.
Media Attributions
- Multiply fractions