3 The Four Operations with Fractions

When you use the four processes with fractions, they behave like whole numbers and decimal numbers, and there are calculators available to do fraction calculations. This is a worthwhile investment for a baker. If you don’t have access to a kitchen calculator or another calculator that has fraction functions, here is a helpful link you can use to do fraction calculations: Calculator Soup You may use this link for assignments and quizzes in this class.

Addition and subtraction word problems with fractions are done the same way as other word problems. Here are a couple of examples:

If the recipe calls for cup of sugar, and cups of brown sugar, how much sugar will there be in total?

          There will be a total of cups of sugar used in the recipe.

If there are 6 cups of rice in the box, and you use cups of rice, how much rice will be left in the box?

          There will be cups of rice left in the box.

Many multiplication problems with fractions are done in the same way as other word problems, as well. For example:

If the recipe calls for teaspoons of vanilla, and you want to triple the recipe, how much vanilla will you use?

          You will use teaspoons of vanilla.

There is another type of fraction multiplication problem, in which the word “of” is used. For example, if you say, What is of 5? you are really saying, What is     The answer would be

Example: If you have a two-quart bottle of oil, and you want to use of it, how much oil would you use?

            You will use quarts. 

Many division word problems with fractions are done in the same way as other word problems. For example:

If there are   cakes, and you want to divide them evenly between two people, how much cake would each person get?

            Each person will get cake.

There is another type of fraction division problem, and that is dividing by a fraction. It’s important to understand what it means to divide by a fraction. For example, the problem      is really saying, “How many   are there in ?” In other words, if you have a half of a cake, how many eighth-sized pieces could you cut from that cake?

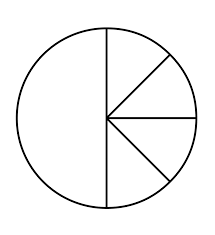
There are four   in .

THE ORDER OF FRACTIONS IN A DIVISION PROBLEM MAKES A DIFFERENCE! The first fraction in the problem is what you are starting with, and the second fraction is the value of the size or quantity you want to divide what you started with into.

This puts an anchor at the top of the page to link to within the page.

This is the Navigation section at the top of the page.

Assignment

Purpose

Outcomes

Instructions

Tips for Success

Fractions Assignment

1) If there are   cups of sugar in the bag, and I use cups of sugar in my recipe, how many cups of sugar will be left in the bag?

2) If the recipe calls for teaspoons of almond extract, and you want to triple the recipe, how many teaspoons will you use?

3) The jar of applesauce contains cups. The can of applesauce contains cups. How many cups of applesauce will you have if you combine the jar and the can?

4) Bashir has three cakes, and he wants to cut them into -sized pieces. How many pieces will he be able to cut?

5) Amanda is making a glaze that makes a total of cups. If she wants to divide the glaze between three pans of cinnamon rolls, how much glaze will she put on each pan?

6) If the bottle contains quarts of oil, how many quarts would   of the bottle be?

7) Luz made five pies for the party. If she cuts the pie into   -sized slices, how many slices will she have?

8) If one recipe calls for  teaspoons of salt, and another recipe calls for   teaspoons of salt, how much salt will Ming use if he makes both recipes?

9) If the recipe for peach melba will make   servings, how many servings will you make if you double the recipe?

10) The bottle of lemon juice contains 42 fluid ounces. How many ounces will be left if you use   fluid ounces in a recipe?

11) If a stick of butter is 8 tablespoons, how many tablespoons are in   of a stick of butter?

12) Alonzo has   cups of cinnamon sugar. If he wants to sprinkle it over five trays of cookies, how much sugar will he sprinkle over each tray?

13) Betty has 12 apples, and she wants to cut them into   -sized wedges. How many wedges will she cut?

14) If the cake recipe calls for   sticks of butter, how many sticks of butter will you need if you want to make three cakes?

15) Jamal is making an icing that calls for   tablespoons of vanilla, and a cake that calls for   tablespoons of lime juice. How much vanilla will he need all together?

16) If there are   pints of half and half in the pitcher, and you want to divide it between four creamers, how many pints of half and half will you put in each creamer?

17) If there are 8 ounces of tea leaves in the tin, and you take out   ounces to make tea, how many ounces of tea will be left in the tin?

18) If the recipe calls for   cups of flour, and you want to make half of the recipe, how many cups of flour will you use?

19) If there are 12 cups of sugar in the bag, and you use   cups of sugar, how much sugar will be left in the bag?

20) Kendra is making one cake that calls for   sticks of butter, and another cake that calls for   sticks of butter. How many sticks of butter will she need all together?

21) If you have 18 fluid ounces of orange juice in the pitcher, and you want to pour of the juice into a glass, how many fluid ounces of orange juice will you pour into the glass?

22) If there are   pies left over from the party, and Sam wants to divide the leftovers into   -sized pieces, how many pieces will he cut?

23) If the recipe makes   cups of pudding, and you want to divide it between 5 bowls, how many cups of pudding will be in each bowl?

24) If the recipe for tarts calls for   cup of oil, and you want to make a triple recipe, how many cups of oil will you use?