6 Using Percentages

Percentages are used in many aspects of bakery math. You can visualize percent problems in this form:

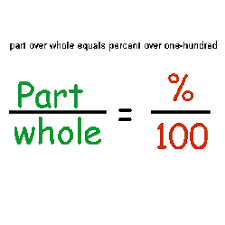
Part over whole equals percent over one hundred

Let’s put this proportion into practice:

What is 20% of 140? You would set up the proportion like this:

LaTeX: \frac{x}{140}\:=\:\frac{20}{100} 

100x = 140 LaTeX: \times 20

100x =2800

x = 28

 

What percent of 250 is 30?

LaTeX: \frac{30}{250}\:=\:\frac{x}{100} 

250x = 30 LaTeX: \times 100

250x = 3000

x = 12

 

90 is 30% of what number?

LaTeX: \frac{90}{x}\:=\:\frac{30}{100} 

90 LaTeX: \times 100 = 30x

9000 = 30x

300 = x

 

With word problems, it is very important to pay close attention to the wording in order to solve them correctly. The easiest way to tell the difference between part and whole is that the number that comes after “of” is the whole.

There are 30 pounds of potatoes in the bin. Three pounds of potatoes are rotten. What percent of the potatoes are rotten?

You can rewrite this problem as: What percent of 30 is 3?

LaTeX: \frac{3}{30}\:=\:\frac{x}{100} 

100 LaTeX: \times 3 = 30x

300 = 30x

10 =x

10% of the potatoes are rotten.

 

Two cases of apricots cost $40. The wholesaler is giving you a 5% discount. How much will the discount be?

You can rewrite this problem as: What is 5% of 40?

LaTeX: \frac{x}{40}\:=\:\frac{5}{100} 

100x = 40 LaTeX: \times 5

100x = 200

x = 2

You will get a $2 discount.

 

Unemployment tax is 3% of a worker’s base wages. If the bakery owner pays $0.45 per hour in unemployment tax for a baker’s assistant, what are the assistant’s base wages per hour?

You can rewrite this problem as 0.45 is 3% of what?

LaTeX: \frac{0.45}{x}\:=\:\frac{3}{100} 

0.45 LaTeX: \times 100 = 3x

45 = 3x

15 = x

The assistant’s base salary is $15 per hour.

This puts an anchor at the top of the page to link to within the page.

This is the Navigation section at the top of the page.

Purpose

To practice finding missing values in percent problems by using a proportion.

Outcomes

By completing this assignment, you will be able to…

  1. Read and understand real-world percent problems related to bakery math.
  2. Correctly set up the problems as proportions and solve for the missing value.

Instructions

To complete this assignment…

  1. Read the problems you are given.
  2. Determine what value you need to find, and set up the problem as a proportion.
  3. Solve the problem.

 

Tips for Success

To help in the completion of this assignment, make sure to:

  • Read carefully to understand what value is missing.
  • Round all answers to the nearest hundredth, if necessary.

Percentages Assignment

1) The capacity of the banquet room is 150 people. How many people are seated in the room if it is at 60% capacity?

2) About 52% of a pineapple is usable in food preparation. If Sahra prepared 33.8 ounces of pineapple chunks, how many ounces of whole pineapple did she begin with?

3) If you buy products valued at $342.57, and the wholesaler is giving you an 8% discount, how much will be discounted from this price?

4) Nimo bought a carton of strawberries, and he discovered that 35% of the strawberries were not yet ripe. If 4.2 pounds of strawberries were not ripe, how many pounds of strawberries were in the carton?

5) If the restaurant bill was $72.65, and the guest leaves a tip of $14.53, what was the percentage of the tip?

6) If the bake shop owner pays 2% of the server’s wages for worker’s compensation, how much will the owner pay per hour if the server’s wages are $2.24 an hour?

7) The bakery has 12 servers scheduled to be on duty. If 3 servers call in sick, what percentage of servers is that?

8) If the rental fee for the kitchen was discounted 20%, and the discount was $48, what was the original rental fee?

9) If there are 54 apples in the crate, and 13 of these apples are bruised, what percentage of apples is bruised?

10) About 50% of cantaloupe is usable in food preparation. If Joe buys 25.52 pounds of cantaloupe, how many pounds of cantaloupe will he be able to use?

11) The restaurant is at 60% capacity. If there are 36 people in the restaurant, what is its full capacity?

12) If the utilities rate for the month increased by 12%, and the bill last month was $354, how many dollars did the bill increase this month?

13) If there are 30 pounds of apples in the bin, and 5 pounds of potatoes are too small to make baked apples, what percentage of apples is too small?

14) Sarah’s bakery donated $580 to charity last year. If the bakery made a profit of $12,421, what percentage of the profit did Sarah donate to charity?

15) Don got a discount of 10% from the wholesaler. If his discount was $14.32, what was his bill before the discount?

16) If the restaurant bill was $124.63, and the diner wants to give a 25% tip, what will the tip be?

17) About 82% of carrots is usable in food preparation. If Cara prepared 61.2 ounces of carrots for carrot cake, how many ounces of carrots did she start with?

18) Naima owns a large bakery that employs 3 salaried employees out of a total of 36 staff. What percentage of the staff is salaried?

License

Icon for the Creative Commons Attribution 4.0 International License

Bakery and Business Math Copyright © by Eunice Graham is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book