5 Ratios and Proportions
A ratio is used to show a relationship between two numbers. The numbers are separated by a colon ( : ) as in 1:2.
The relationship can represent something as simple as the 1:3 ration commonly used to mix frozen juices. We use 1 can of frozen juice concentrate to 3 cans of water. This is an example of a part-to-part ratio. You can also have part-to-whole ratios. For example, the ratio of frozen juice concentrate to reconstituted juice is 1:4, that is, 1 can of concentrate to four cans of total reconstituted juice.
Proportions are two equivalent ratios in which the terms of the first ratio have the same relationship as the terms of the second ratio. For example, 1 cup of butter to 3 cups of sugar (1:3) is in proportion to 2 cups of butter to 6 cups of sugar (2:6). The easiest way to visualize proportions is to write the ratios in fraction form, like this: Notice that in this proportion, the butter is on top, and the sugar on the bottom in both ratios. This is a helpful way to check that you are setting up a proportion correctly.
To solve for an unknown number in a proportion, you cross multiply, like this:
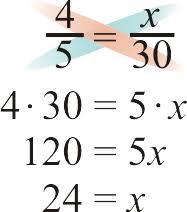
So let’s say that you are using a recipe of 2 teaspoons of vanilla for 3 cups of sugar. If you want to change the recipe so that it uses cups of sugar, how much vanilla would you use?
2
= 3
9 =
3
You would use 3 teaspoons of vanilla.
If 12 eggs cost $1.49, how much to 18 eggs cost?
If one can serves 2.5 people, how many cans serve 10 people?
Sometimes proportions that contain fractions can be confusing, but they are solved in exactly the same way:
One way we use proportions in cost analysis is by finding the unit rate and seeing which of two options would be the better buy. Let’s say one store has a 24-ounce jar of applesauce for $6.55, and another store has a 45-ounce jar for $13.40. Which is the better buy? What you would do is find the unit price for each jar. The first jar:
1 $6.55 = 24 ounces
? 1
$13.40 = 45 ounces
?
$6.55 = 24 ounces ? $13.40 = 45 ounces
?
$0.272 . . . = ? $0.297 . . . = ?
1 ounce of applesauce = 1 ounce of applesauce=
27 cents (round to the nearest hundredth) 30 cents (round to the nearest hundredth)
The 24-ounce jar is the better buy!
This puts an anchor at the top of the page to link to within the page.
This is the Navigation section at the top of the page.
Assignment
Purpose
To practice reading and solving ratio and proportion word problems relating to bakery math.
Outcomes
By completing this assignment, you will be able to…
- Read ratio and proportion word problems for understanding.
- Correctly set up and solve ratio and proportion word problems.
Instructions
To complete this assignment…
- Read the problems carefully and find the correct answers.
- Be sure to show how you set up each problem.
- Use fractions for common volume measures (cups, teaspoons, etc.) and decimals for weights (grams, ounces, pounds) and money. Round decimals to the nearest hundredth.
Tips for Success
To help in the completion of this assignment, make sure to:
- Read each problem carefully and understand what it is asking.
- Understand whether to use a fraction or a decimal for your answer.
- Include how you set up each problem in order to get credit.
Ratios and Proportions Assignment
1) If you are using a recipe that has the proportion of 1 cup of butter to 3 cups of sugar, how many cups of butter will you need if you will be using 8 cups of sugar?
2) Maria is going to make a glaze that has the proportion of 3 tablespoons of powdered sugar to 1 teaspoon of milk. If she wants to use 4 teaspoons of milk, how much powdered sugar should she use?
3) I want to make a caramel icing that has the proportion of cup of packed brown sugar to
cup butter. How much brown sugar should I use if I use
cups of butter?
4) Yesenia is going to make a salmon glaze that has the proportion of 2 tablespoons of lemon juice to cup of soy sauce. How many cups of soy sauce should she use if the uses 3 tablespoons of lemon juice?
5) Mitch has a recipe for cake icing that has the proportion of 3 cups of confectioners sugar to cup of butter. How much butter should he use if he uses
cups of confectioners sugar?
6) The recipe has the proportion of 1 tablespoon of baking soda to 3 pounds of flour. How many pounds of flour should you use if you want to use tablespoons of baking soda?
7) If a dozen eggs costs $1.60, how much would 8 eggs cost?
8) If a dozen doughnuts costs $8.99, how much would 18 doughnuts cost?
9) If 6 cans of soda cost $2.75, how much would 24 cans of soda cost?
10) If 8 bakery cookies cost $14, how much would 12 bakery cookies cost?
11) If a dozen dinner rolls cost $3.99, how much would 32 rolls cost?
12) If 8 meat pies cost $8.72, how much would 6 meat pies cost?
13) If a 19-fluid ounce bottle of dish soap costs $2.89, and a 40-fluid ounce bottle costs $5.79, which one is the better buy?
14) If a 32-fluid ounce bottle of lemon juice costs $3.29, and a 48-fluid ounce bottle costs $6.99, which one is the better buy?
15) If a 20-ounce bottle of vegetable oil costs $2.99, and a 32-ounce bottle of vegetable oil costs $3.19, which one is the better buy?
16) If a 29-ounce can of peaches costs $2.99, and a 15-ounce can of peaches costs $1.89, which one is the better buy?
17) If a 2-pound bag of flour costs $1.89, and a 5-pound bag of flour costs $3.86, which one is the better buy?
18) If a 26-ounce canister of salt costs $0.99, and a 64-ounce box of salt costs $1.69, which one is the better buy?

