3 Maps and Models
“Two important characteristics of maps should be noticed. A map is not the territory it represents, but, if correct, it has a similar structure to the territory, which accounts for its usefulness.” – Alfred Korzybski, Born Jun. 3, 1879. [Bold face added for emphasis by C. McCormick]
About the quote:
Alfred Korzybski was a Polish-American philosopher-scholar. The quote “The map is not the territory.” is generally attributed to him. In this geography course, that idea has direct application to the effective use of maps.
But the quote has much broader applications as well. Don’t limit the usefulness of the concept to strictly ‘territory of land’. He’s using ‘territory’ to represent any portion of reality, and ‘map’ as any incomplete representation of that reality. For him a ‘map’ can include a written description, mathematical model, mental image, or other impressions. He’s saying we should beware of the limitations of simplifications and consider the source of information.
MODELS
Maps are models of reality. As models, they simplify and generalize the actual situation. Map makers, called cartographers, must decide on the intended purpose of the map in order to determine what data is necessary to achieve the intended purpose. Data that is unnecessary or distracting should be removed. For instance a highway map of an entire state will not show individual trees because the trees are not necessary for determining the routes along roadways.
GRAPHICACY
Literacy refers to the ability to read, write, and use words. Geographers often find it more efficient to convey concepts by using maps and diagrams. Graphicacy refers to the ability to effectively use, interpret, and create maps and diagrams. The sciences regularly use diagrams. A graphically literate person should recognize the shortfalls and advantages of different types of diagrams. A graphically literate person can “read” images.
Maps are a specific type of image. Maps show how data and characteristics change across space. All geographic data has a spatial component. It must have some type of location information associated with the data. A column graph showing two or more cities and their corresponding burglary rates is a valid graphical depiction of geographic data. The geographic location data is each of the cities. However, as you plot more and more cities on the column graph, it becomes more difficult to read. Good graphics should make it easier for the user to get the desired information. Plotting several dozen, or several thousand, cities on a single column graph would become incomprehensible. A map is much easier to read.
Things to keep in mind when reading maps and models:
- The map is not reality.
- The intents and biases of the cartographer.
- Maps can influence reality.
Since maps are models, they will by necessity not contain all aspects of a region. One map may show political boundaries, but not the topography while another will show topography, but not political boundaries. Both can be good maps depending on who is reading them, or who is making them.
The cartographer needs to decide what information is important to include and what can be deleted. That decision is based on the intended purpose of the map and sometimes that purpose is to deceive the map user. Consider the intentions of the cartographer!
Sometimes people try to make reality conform to the model. This can be good, such as a landscape gardener using a map to determine where to place plants. But sometimes a map is made as a general average depiction of multiple areas and it’s impossible for that average to truly exist. There are too many variables, including changing over time, for them all to align as a perfect unchanging reality. City planners create models and goals, but good planners recognize that preferences for how to use the land can change over time as technology changes and the needs of the population changes.
SCALE (Distance)
Scale is the degree of generalization of a map. There are three ways of indicating map scale: verbal scale, representative fraction, and graphical scale. The verbal scale is an old form, rarely used since about WWII. It is simply writing the scale in words: “One inch is approximately six miles”.
The representative fraction (RF) scale is mathematically consistent across the map. To use the RF scale, you must have a ruler. The RF scale is written as a ratio (1:24,000) where there first number is always ‘1’ and is the distance measured with a ruler on the map. Multiply that number by the second number (in the example it’s 24,000) to find the true ground distance. Remember to consider significant figures when using the RF scale. The result is the actual ground distance between the two points, with the same units as you used with the ruler. Notice the RF scale has no units in it, so whichever units you use when measuring on the map (mm or cm or inches) is the same units on the ground.
An example: What is the ground distance between two intersection shown on a map? Map distance between intersections (use ruler): 4 inches. The map has an RF scale of 1:24,000.
(map distance ) x (RF scale) = (ground distance)
4 inches × 24,000 = 96,000 inches between the two intersections on the ground.
That’s a lot of inches, so it may be useful to change to different units of length.
[latex]96,000 in \times \frac{1 ft}{12 in} = 8,000 ft[/latex]
[latex]8,000 ft \times \frac{1 mi}{5280 ft} = 1.5 mi[/latex]
The third scale is a graphical scale. This is especially common in the era of photo copiers. If a paper map is photographically enlarged or reduced, but the graphical scale is included in the same process, then the graphical scale is still accurate whereas the verbal and RF scales are no longer accurate after enlarging or reducing.

To use a graphical scale, a ruler may be used, but it’s not necessary. Any piece of paper will work. Place the edge of the paper along a line between the two points of interest and mark their locations on the edge of the paper. Now bring the paper to the graphical scale and note where the two points align on the scale.
Different maps have different scales. Maps are either large scale or small scale. There is no predefined limit where small scale shifts to large scale. It is a relative term. One map is smaller scale compared to (in relation to) a second map. Larger scale maps show less area in more detail than smaller scale maps. This is easier to explain using the RF scale. A map of RF scale 1:2 shows more detail than a map with scale 1:4. The first map is a larger scale than the second map. Mathematically, 1/2 is greater than 1/4. When we talk about large- and small-scale maps and geographic data, then, we are talking about the relative sizes and levels of detail of the features represented in the data. In general, the larger the map scale, the more detail is shown. Photographs and images do not have consistent scale throughout the entire displayed area. This can be corrected mathematically so that a single scale is correct. The correction, called orthorectification, alters the image so it appears as if the map user is directly overhead of all points on the map rather than overhead of one point and viewing other points from a slight angle. USGS topographic maps are developed from images that have been orthorectified.
AREA
The area on the map relates to area on the ground based on the map scale. The USGS makes several series of maps using standard scales and there are inexpensive tools that you can buy to quickly estimate area on those standard map scales.
As with so many of life’s problems, you probably won’t know the answer before you start. But often you can find a region of possibilities. From basic geometry you know there are formulas for finding the area of regular shapes such as squares, circles, and polygons. Even if you’ve forgotten what the formulas are, you know they exist. The difficulty with natural shapes on maps is they are regular polygons and those formulas won’t work.
There are many methods for estimating the area of irregular shapes, but most of them work on the idea of finding the area of a simple shape such as a square or rectangle and fitting those in the irregular shape.
Find the maximum possible and an approximate minimum area for the shape.
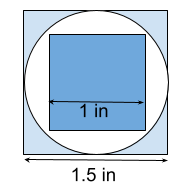
The maximum area. Create a regular polygon (square, rectangle, maybe a circle) that is larger than the irregular shape. In the figure to the right, we are estimating the area of the circle. We can see that area of the circle is smaller than the area of the large, light blue, square because the circle is entirely within the large square. That square has an area of 1.5 in x 1.5 in = 2.25 in2. Since the circle is entirely within that square, we know the area of the circle is less than 2.25 in2. Note: the large square doesn’t have to touch the circle, but getting it closer will narrow your error range.
Now find a minimum. First you know the shape exists in space because it’s shown on the map so the area will certainly greater than zero. But you can do better. Put another, smaller, regular shape entirely within the irregular shape. Here the dark blue square is entirely within the circle. The area of the square is 1 in x 1 in = 1 in2. You know the area of the circle is greater than 1 in x 1 in = 1 in2. NOTE: I wouldn’t spend too much time on the minimum. I’d probably find the maximum then move on the the next step of using small squares.
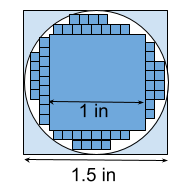
To get a better estimate of the area of the irregular shape, use smaller squares! In this example the small squares are 0.1 in x 0.1 in. = 0.01 in2. As drawn, even with the smaller squares, we know we will under estimate the area of the circle because all of the squares fit inside the circle and there’s still white space visible and none of the light blue is covered. There might be a situation where it’s important to know that you’ve under estimated the area. In another situation you may want to be sure you’ve over estimated (you don’t want to run out of sod for the lawn) so you would make sure there’s no white area visible by adding more small squares.
If you want a good estimate, but aren’t concerned if you’re either over- or underestimating, then draw small squares along the edge of the circle so some squares are more within the circle and others are more outside the circle and estimate when you have an entire square’s worth. Three squares that are each only 1/3 within the circle will add up to 1 full square.
How small is too small? Once again it depends on the map scale, what your needs are, and the precision of other measuring tools. If you’re drawing squares by hand even the thickness of the pencil might be a large portion of the area of the small circles. That’s bad.
Here’s an actual lake estimate:
Maximum area. McDougal lake is entirely within the square that measures 1 in x 1.25 in on the map. The scale is 1:18,000 or 1in = 0.2mi.
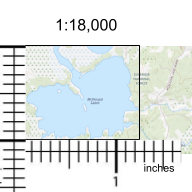
Convert from map length and area to ground area:
One side of the rectangle is: 1 in = 0.2 mi on the ground
The side of the rectangle is: 1.25 in x 0.2 mi/in = 0.25 mi on the ground
Ground area covered by the rectangle is 0.2 mi x 0.25 mi = 0.05 mi2
Ground area: 0.05mi2 x 640ac/mi2 = 32 acres (in the USA acres is a common unit of measuring surface area).
We now know the area of the lake is less than 32 acres.
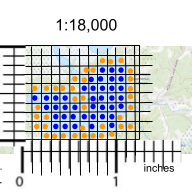
In the image to the right, each small square is 0.1 in x 0.1 in so 0.02 mi x 0.02mi = 0.0004 mi2 x 640ac/mi2 = 0.256 ac (about 1/4 acre per square).
Each square with a blue dot is entirely water. There are 40 of them: 40 squares x 0.256ac /square = about 10 acres. Since all those squares are entirely water, this is a minimum area estimate.
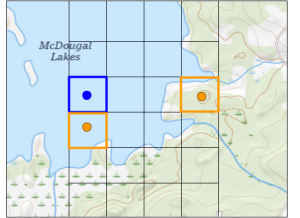
Each square with an orange dot has some water and some land. I estimate they are equivalent to about 31 fully water squares: 31 sq x 0.256 ac/sq = 7.9 acres. You might simply take a ballpark estimate that 1/2 of the area of these squares is water. Another option is to make an eyeball estimate and combine squares of differing water area so they sum to one full square. In the image to the right the blue square and blue dot is 100% water. One of the orange squares is nearly all water while the other orange square is nearly all land. Estimate one as 90% water and the other as 10% water and you have one square at 100% water.
Total lake area estimate:
10 acres (minimum based on squares with blue dots)
Area of 34 orange squares:
Water area if all orange squares are 100% water: 34 sq x 0.256 ac/sq = 8.7 ac
Area of orange squares if 50% water: 8.7ac/2 = 4.35 ac
Area of orange squares by ‘eyeball and combine’: 7.9 acres
A second method (or check your work):
In the image with the small squares and dots, there are 10 rows of squares and 12.5 columns (the far right column is half-width), for 10 x 12.5 =125 squares.
We counted a total of 40 + 31 = 71 squares of water. 71 water squares/125 total squares x 32 acres = 18.2 acres of water. It’s not exactly the same due to some rounding, but both estimates are valid.
Based on my personal knowledge of lakes in the mapped region, this seems like a plausible approximation.
Conclusion: The lake has an area of at least 10 acres, no more than 18.7 acres, and quite likely about 17.9-18.2 acres. If you need to, and your data and tools justify it, you can make smaller squares to make a better estimate. Students in precalculus might be familiar with this method.
DIRECTION
Direction is one of the three key concepts in geography. When I would fill in as a bus dispatcher, drivers would occasionally call or radio to ask for directions. After a few calls, I got to know which drivers preferred to use street and building names and which drivers preferred to use compass directions and distances. Both methods work. Both drivers picked up and delivered passengers just fine.
Relative directions use local landmarks that presumably will be known or obvious to the person receiving the instructions. An example might be “Turn left at the tallest building in town. No other building comes close to its height.” That example includes an obvious landmark, (the tallest building), and a relative direction (left). ‘Left’ is a relative direction because a person arriving at the building from the opposite direction would turn right instead of left.
Absolute directions use compass directions such as north, south, east, west. Technically, even those directions are relative to the earth’s magnetic poles and and axis of rotation, but we won’t quibble with that. From the previous example, the word ‘left’ could be changed to ‘north’. With that change, everyone knows to turn north at the building and you don’t need a second set of instructions for people arriving at the building from different directions. But you do need to know which way is north!
With the proper tools, and if your needs demand it, you can provide compass directions to fractions of a degree of arc just like degrees of latitude and longitude are divided into minutes and seconds or into decimal fractions of a degree. However, your tools such as the map scale and manufacturing tolerances of the compass or surveying instruments must be up to the task of such precision.
If you’re finding directions on a map, you don’t truly need a compass. A protractor will work for an estimate within a few degrees when using a 1:24,000 scale map. Set your protractor on the map with the 0° marker aligned with the north direction of the map. On the map, draw a line connecting the two points you’re interested in. Put the center of the protractor on one point, or anywhere along that line, but maintain the orientation of the protractor so 0° is still parallel to north. Read where the line intersects the numbers, the degrees, on the protractor. The line could intersect the protractor at two locations. Think which direction you’re determining. You may want to start goin 135° (southeast) but if you reverse your direction, you be going 315° (northwest).

Once you’re outdoors, you’ll need a compass. Find north so the red arrow on the compass overlaps the printed arrow on the rotating housing of the floating arrow. That housing has degree marks written on it. With one hand hold the housing to keep the arrows aligned. With the other hand rotate the base of the compass (usually transparent) until the direction arrow on the base aligns with the degree direction you want to follow. Walk the direction of the large arrow on the base while keeping the magnetic arrow hovering over the arrow in the housing.
Compass Directions: Azimuth or Bearing
There two methods to write a compass direction: Azimuth or Bearing
-
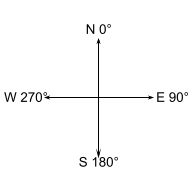
Diagram of major AZIMUTH directions. A compass AZIMUTH is where due north is always 0° and values increase clockwise. Due east is 90°, due south is 180°, due west is 270°. The maximum possible value for AZIMUTH is 360°, which is also due north, but is usually labeled as 0°.
- It’s understood that due north is always the starting point and values always increase clockwise, therefore there’s no need for including a direction (north south east west) in the azimuth.
- The yellow compass above has an azimuth of 135°
-
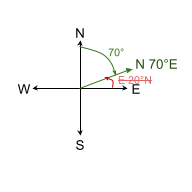
How to derive the Bearing. In a compass BEARING, N or S is given first, then a degree to an adjacent cardinal direction (E or W) is given second.
- Example: A direction of 70° has a BEARING of N70°E. The dominant cardinal direction is N but you go east, specifically 70°.
- Bearing: N70°E is correct. E 20°N is wrong. As azimuth that bearing is written: 70°
SLOPES
Slopes are a means of comparing quantities two different variables. In geography, slopes are often used to express how a characteristic changes over space or over distance. The word ‘over’ in the previous sentence should immediately indicate there is division involved and that the x-axis (horizontal) will often be labeled as some form of distance or location.
Why use slopes? Consider some basic concepts of science such as energy forms, concentration, and distribution. By manipulating your point of view, perhaps from an overhead map view to a side profile view, you might better understand these characteristics of energy. A rock at a mountain top has more potential stored energy than a rock on the valley bottom. If the slope is steep, meaning the mountain top and valley bottom are close together with a large difference in elevation, then that potential energy is more likely to convert to kinetic energy as the rock falls to the valley floor. One of the laws of physics says that energy moves from high concentration to low concentration. Slopes help visualize, quantify, and location where those high and low concentrations happen and the direction of movement of energy. The energy may be embedded in air, rock, or water, or wheat or many different things.
There are many correct ways of expressing slope but they are all essentially:
[latex]\frac{Rise}{Run} = slope[/latex]
Some Review:
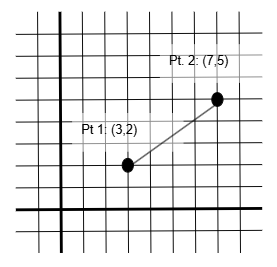
From an algebra class you may recall that points are written in (X,Y) format. The rise is the difference in y components and run is the difference in x components. ‘Difference’ means subtraction. In the figure to the right, the two points are located at (3,2) and (7,5).
Rise is (5-2)=3
Run is (7-3)=4
Slope is ¾.
How to determine slopes using a topographic or other isoline map
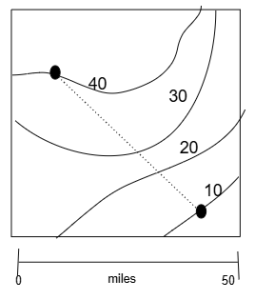
There is a big difference when finding the slope on a topographic map. On a topographic map, when you move right-left you’re probably changing your east-west location and when moving up-down on the map you’re changing the north-south location. If you use that information, you can find a correct slope, the math works, but that’s probably not the correct slope you want to find because you used the wrong data. The data you used was latitude and longitude data, instead of elevation and distance data.
To find the slope of the land surface, you need the starting and ending elevations and the distance between them. Calculate the rise by using the contour lines. The run is found by using the scale.
Find the rise. This is the change in elevation.
Use the contour lines to find the top elevation and the bottom elevation. Subtract the bottom elevation to get the change. There is some room for variation in values. If a point is between contours of 30ft and 40ft, you only know the elevation is somewhere between 30 & 40ft. Since the locations of interest in the diagram above are exactly on the contour lines, we’re lucky.
Point 1 Elevation: 40 ft
Point 2 Elevation : 10 ft
Rise: 40 ft – 30 ft = 20 ft
Find the run. This is the horizontal distance between the two points
- You must determine the Ground Distance (often in units of ft, m, km, or mi).
- Use the map scale to find the real ground distance between the two points.
Using the graphical scale in the diagram the distance between the points is 50 miles. (I held a piece of paper to my screen, aligned it with the dots and marked their location on the edge of the paper, then held that paper along the graphical scale below the map.)
Calculate the slope
Rise: 20 ft
Run: 50 mi
Slope: [latex]\frac{Rise}{Run} = \frac{20 ft}{50 mi}[/latex] =0.4 ft/mi
Units!
Notice how the final slope answer has both feet and miles in the answer. There are always two things changing with slopes: the rise and the run. You must have the units for each of them, so your answer will have two units of measurement.
Mathematically, when the same units are on top and bottom (numerator/denominator) they cancel each other out and the result is simply ‘1’. Remember anything divided by that same thing is always 1. That means you end up with an answer that has no units of measurement. In this case, if the numerical value of the answer is small and several places to the right of the decimal point, you might multiply by 100. If you multiply by 100, the answer is expressed as % implying for each single unit of rise, there are 100 units of run. So instances when there are no units in the slope may be written as % or even as ‰ (if multiplying by 1000).
Because slopes written as %, ‰, have no units, you can choose which units to use, but you must use the same units in both rise and in run.
% (percent): use only if both the rise and the run are in the same units such as feet/feet. Remember to multiply by 100, but only multiply once. Quite often I see people incorrectly multiply by 100 two times. A 5% slope means for every 100 feet of run there’s a 5 foot rise. If you use meters instead of feet, it still works the same: 100 m of run and 5 m of rise.
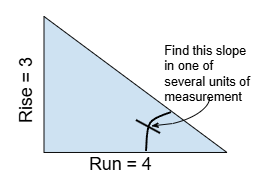
From the diagram to the right:
3ft/4ft=0.75 (ft/ft cancel out)
0.75 x 100 = 75% slope
‰ (per mille): exactly the same as % but here the run is 1000 units not 100 units. This is the same as m/km.
3ft/4ft=0.75 (ft/ft cancel out)
0.75 x 1000 = 750‰ slope
OR in metric:
3m/4km =0.75m/km
0.75 m/km x (1 km/1000 m) = 0.00075
0.00075 x 1000 = 750‰
Ft/mile: often used in gentle slopes like railroads or rivers. For every mile the river goes, it drops so many feet. In the metric system, you often have m/km which is identical to the per mille discussed earlier.
ft/mile uses Imperial units, the metric system equivalent is usually m/km which is identical to ‰ or per mille since there are 1000 m in 1 km.
Do the final division of the numbers so the denominator is 1 mile. You do the calculation so it’s easier to compare different slopes since you always have the same run (1 mile), only the rise changes. The denominator value is always 1, but the units will change.
30ft/3 miles is wrong, 3 ft/mi is correct.
3ft/4mi= 0.75 ft/mi (different units for rise and run, don’t cancel)
Ratios: for example 3:4 this SHOULD be rise first, run second. Unfortunately, I often see this reversed.
SYMBOLS
Maps contain symbols to represent different portions of reality. Common types of symbols are point, line, and area symbols.
All three classes of symbols have variations that are better able to indicate changes in either quantity or quality of the represented characteristic. Quantity is often shown by changing the size of the symbol. If a circle represents a town, a larger circle indicates a larger population. To show different types of features (changes in quality), the shape of the symbol is changed. A circle can be a town, a small airplane represents an airport, and an anchor could be a harbor. Color intensity (shading) is often used for quantitative change, but changes in color hue (red or green) generally indicate a change quality.
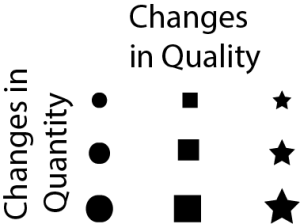
As the scale and generalization of maps change, some symbolic representations of reality might change. For instance a small scale map of Iowa that is printed in a notebook would probably use a point symbol to indicate the location of cities. But a map of Des Moines, IA on the same size piece of paper would use an area symbol for the entire city.
MAP TYPES
Scales and symbols are used in all types of maps. Maps are broadly categorized as either reference maps or as thematic maps. Reference map display a broad range of characteristics and try to give equal value to all of them. Topographic maps are a type of reference map that depict the lay of the land, including elevation and water bodies. Thematic maps often ignore the topography and landforms to better show other characteristics.
POINTS OF VIEW
Most maps are probably drawn in map view. (Stunning statement!) This is the overhead, from above, view. It’s a good choice for showing how a characteristic changes or moves horizontally. US State highway maps are drawn in map view.
A profile view shows the vertical change of a characteristic. When you stand on the ground and look at buildings from the base to the roof, you’re looking at their profile.
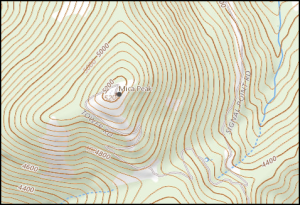
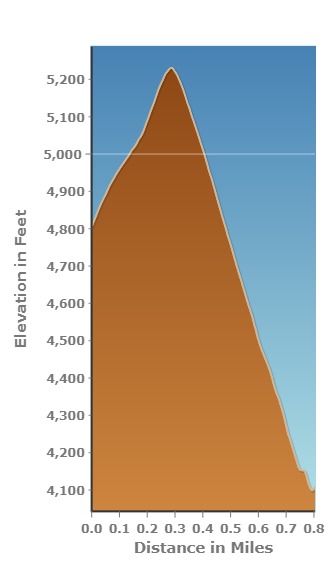
TOPOGRAPHIC MAPS
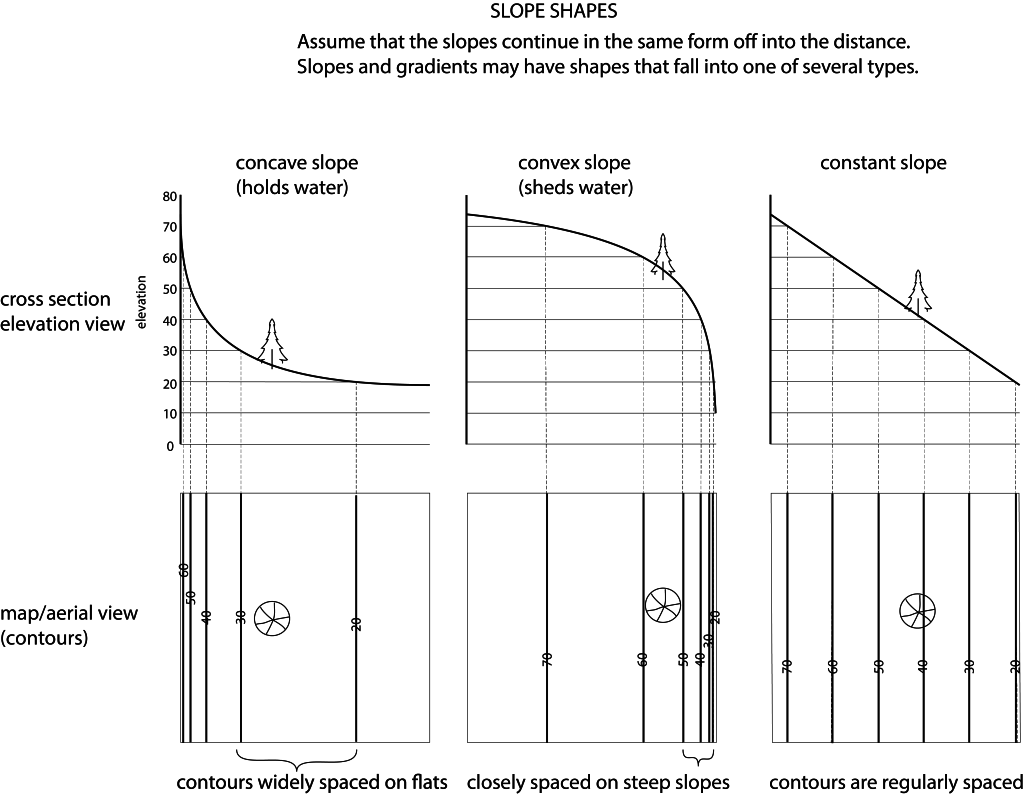
Topographic maps use isolines to indication elevation. Isolines that specifically indicate elevation are called contour lines. Other maps use isolines to show atmospheric pressure. Those lines and called isobars. In the map above and left, the contour lines are a brown color. In general, isolines connect points of equal value. The value can be land surface elevation, depth to the lake or ocean floor, average annual precipitation, or depth of snow in a storm, for a few examples. When isolines are close together, there is a greater change in the characteristic over a short distance. When contour lines are close together, the land surface has a steeper slope. Proficiency with isolines is an important geographic skill. The image below shows how placement of isolines helps indicate slopes.
Isolines are also approximations of reality. A weather map of the entire state seems to tell you what the temperature is at all points. In fact, the temperature was measured only in a few locations and estimates of the temperature for all other points are indicated with the isolines. Isolines indicating temperature are called isotherms. The same process is used to make topographic maps. The USGS has a large number of points with known elevation and location. Using these points, called benchmarks, as a starting point, contours are drawn to indicate the slope of the land surface.
Isolines
Isolines are used to depicted many types of characteristics. Any point along the same line has the same value or quantity of the characteristic. The change in value as you move from one isoline to the immediate adjacent isoline is the interval, even if the value of the lines is only implied and not labeled on the map. To improve map clarity, not all isolines are labeled. Index isolines are labeled.
Here are names for some isolines that depict different characteristics:
- Contour lines: land elevation
- Isobars: atmospheric (barometric) pressure
- Isotherms: temperature
- Isohyets: precipitation

THEMATIC MAPS
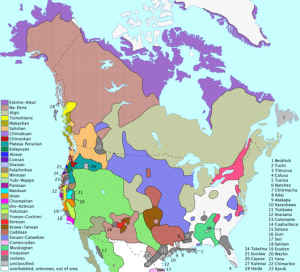
The two maps shown above are both thematic maps. Neither map shows landforms. The map on the left shows how languages were distributed spatially across North America, while the map on the right is showing how crime rates vary by state. They are both good maps. The language map uses color well because no single color stands out as more significant, all colors have the same shade indicating that all languages have similar importance. However, the map reader must beware that languages don’t change as abruptly as the the map might indicate. As you move from southern Minnesota to northern Minnesota, don’t expect an abrupt change in spoken languages from Sioux to Algic. Although such an abrupt change is possible, it isn’t necessarily the case.
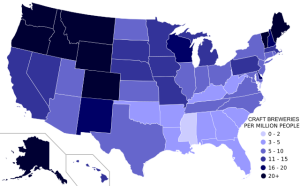
The craft brewery map is good because it uses shades of a single color and the data has been processed properly. The map shows how a single data set (Craft Breweries per capita) changes so it uses a single color in different shades. People naturally associate darker shades with more of a value so the dark blue indicates that the Pacific Northwest has a more breweries per capita. The cartographer also processed the data to improve comparisons among states with different populations and population density. Good choropleth maps such as this use preexisting political boundaries (countries, states, counties) and show data in forms such as breweries per consistent number of people (per capita) or as per consistent unit of area (per mi2 ).
Summary
Maps are models that simplify and generalize the real world. The amount of generalization is the scale of the map. Good use of map symbols can improve the interpretation of the map. There are broad categories of maps that are better suited to demonstrating broad categories of data.

