7.5 Entropy
Learning Objectives
- To gain an understanding of the term entropy.
- To gain an understanding of the Boltzmann equation and the term microstates.
- To be able to estimate change in entropy qualitatively.
- To gain an understanding of methods of measuring entropy and entropy change.
To assess the spontaneity of a process we must use a thermodynamic quantity known as entropy(S). The second law of thermodynamics states that a spontaneous process will increase the entropy of the universe. But what exactly is entropy? Entropy is typically defined as either the level of randomness (or disorder) of a system or a measure of the energy dispersal of the molecules in the system. These definitions can seem a bit vague or unclear when you are first learning thermodynamics, but we will try to clear this up in the following subsections.
The Molecular Interpretation of Entropy
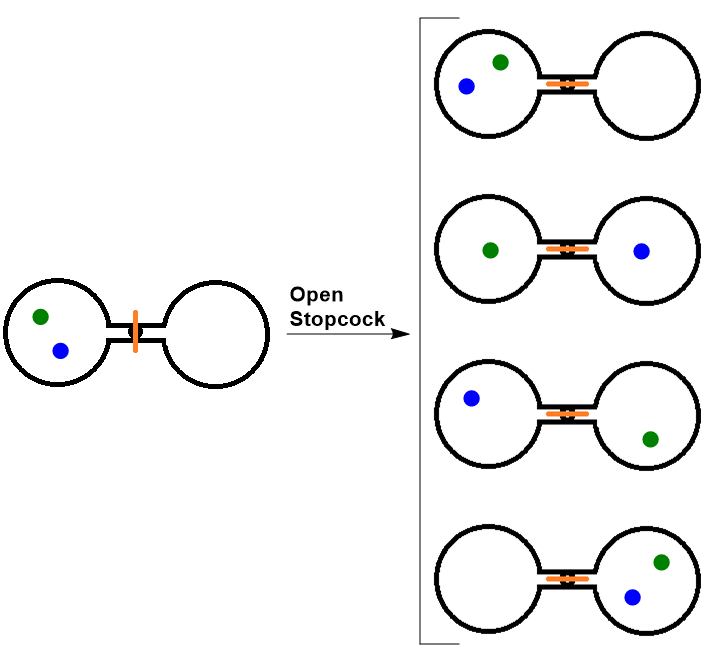
Consider the following system, where two flasks are sealed together and connected by a stopcock (see Figure 7.4 “Two-Atom, Double-Flask Diagram”). In this system, we have placed two atoms of gas, one green and one blue. At first, both atoms are contained in only the left flask. When the stopcock is opened, both atoms are free to move around randomly in both flasks. If we were to take snapshots over time, we would see that these atoms can have four possible arrangements. The likelihood of all atoms being found in their original flask, in this case, is only 1 in 4. If we increased the number of atoms, we would see that the probability of finding all of the atoms in the original flask would decrease dramatically following (½)n, where n is the number of atoms.
Thus we can say that it is entropically favored for the gas to spontaneously expand and distribute between the two flasks, because the resulting increase in the number of possible arrangements is an increase in the randomness/disorder of the system.
The Boltzmann Equation

Ludwig Boltzmann (1844–1906) pioneered the concept that entropy could be calculated by examining the positions and energies of molecules. He developed an equation, known as the Boltzmann equation, which relates entropy to the number of microstates (W):
[latex]S=k \ln W[/latex]
where k is the Boltzmann constant (1.38 × 10−23 J/K), and W is the number of microstates.
Microstates is a term used to describe the number of different possible arrangements of molecular position and kinetic energy at a particular thermodynamic state. A process that gives an increase in the number of microstates therefore increases the entropy.
Qualitative Estimates of Entropy Change
We can estimate changes in entropy qualitatively for some simple processes using the definition of entropy discussed earlier and incorporating Boltzmann’s concept of microstates.
As a substance is heated, it gains kinetic energy, resulting in increased molecular motion and a broader distribution of molecular speeds. This increases the number of microstates possible for the system. Increasing the number of molecules in a system also increases the number of microstates, as now there are more possible arrangements of the molecules. As well, increasing the volume of a substance increases the number of positions where each molecule could be, which increases the number of microstates. Therefore, any change that results in a higher temperature, more molecules, or a larger volume yields an increase in entropy.
To assess the spontaneity of a process we must use a thermodynamic quantity known as (S). The second law of thermodynamics states that a spontaneous process will increase the entropy of the universe. But what exactly is entropy? Entropy is typically defined as either the level of randomness (or disorder) of a system or a measure of the energy dispersal of the molecules in the system.
As the temperature of a sample decreases, its kinetic energy decreases and, correspondingly, the number of microstates possible decreases. The third law of thermodynamics states: at absolute zero (0 K), the entropy of a pure, perfect crystal is zero. In other words, at absolute zero, there is only one microstate and according to Boltzmann’s equation:
[latex]S=k \ln W = k\ln 1=0[/latex]
Using this as a reference point, the entropy of a substance can be obtained by measuring the heat required to raise the temperature a given amount, using a reversible process. Reversible heating requires very slow and very small increases in heat.
[latex]\Delta S=\dfrac{q_{\text{rev}}}{T}[/latex]
Example 7.7
Determine the change in entropy (in J/K) of water when 425 kJ of heat is applied to it at 50°C. Assume the change is reversible and the temperature remains constant.
Solution
[latex]\Delta\text{S}=\dfrac{q_{\text{rev}}}{T}=\dfrac{425\text{ kJ}}{323.15\text{ K}}=\dfrac{4.25\times10^5\text{ J}}{323.15\text{ K}}=1.32\times 10^5\text{ J/K}[/latex]
Standard Molar Entropy, S°
The standard molar entropy, S°, is the entropy of 1 mole of a substance in its standard state, at 1 atm of pressure. These values have been tabulated, and selected substances are listed in Table 7.2 to 7.4 “Standard Molar Entropies of Selected Substances at 298 K”.[1]
| Gas | S°[J/(mol·K)] |
|---|---|
| He | 126.2 |
| H2 | 130.7 |
| Ne | 146.3 |
| Ar | 154.8 |
| Kr | 164.1 |
| Xe | 169.7 |
| H2O | 188.8 |
| N2 | 191.6 |
| O2 | 205.2 |
| CO2 | 213.8 |
| I2 | 260.7 |
| Liquid | S°[J/(mol·K)] |
|---|---|
| H2O | 70.0 |
| CH3OH | 126.8 |
| Br2 | 152.2 |
| CH3CH2OH | 160.7 |
| C6H6 | 173.4 |
| CH3COCl | 200.8 |
| C6H12 (cyclohexane) | 204.4 |
| C8H16 (isooctane) | 329.3 |
| Solid | S°[J/(mol·K)] |
|---|---|
| C (diamond) | 2.4 |
| C (graphite) | 5.7 |
| LiF | 35.7 |
| SiO2 (quartz) | 41.5 |
| Ca | 41.6 |
| Na | 51.3 |
| MgF2 | 57.2 |
| K | 64.7 |
| NaCl | 72.1 |
| KCl | 82.6 |
| I2 | 116.1 |
Several trends emerge from standard molar entropy data:
- Larger, more complex molecules have higher standard molar enthalpy values than smaller or simpler molecules. There are more possible arrangements of atoms in space for larger, more complex molecules, increasing the number of possible microstates.
- Gases tend to have much larger standard molar enthalpies than liquids, and liquids tend to have larger values than solids, when comparing the same or similar substances.
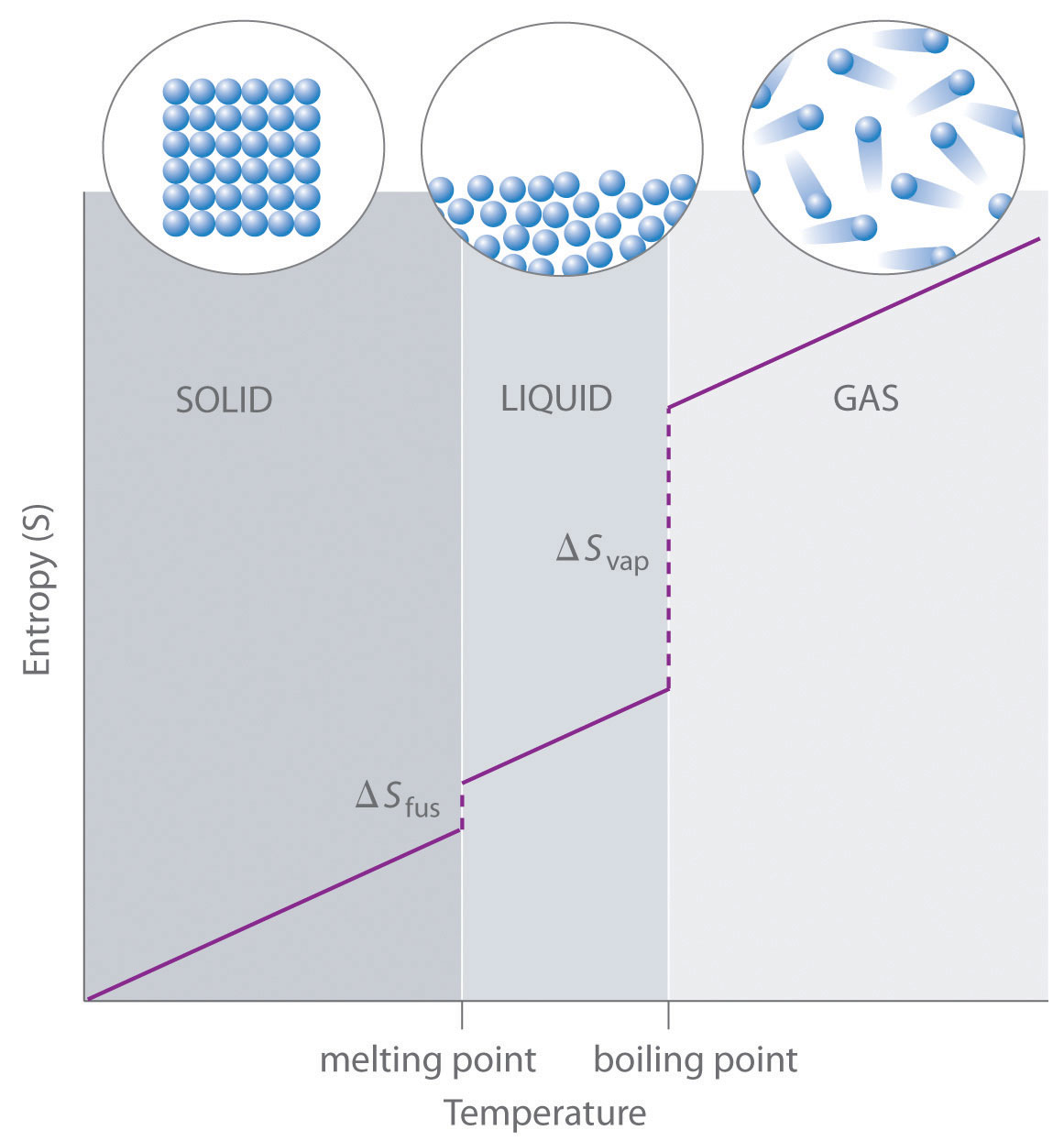
- The standard molar entropy of any substance increases as the temperature increases. This can be seen in Figure 7.6 “Entropy vs. Temperature of a Single Substance.” Large jumps in entropy occur at the phase changes: solid to liquid and liquid to gas. These large increases occur due to sudden increased molecular mobility and larger available volumes associated with the phase changes.
Standard Entropy Change of a Reaction, ΔS°
The entropy change of a reaction where the reactants and products are in their standard state can be determined using the following equation:
[latex]\Delta S^{\circ}=\underset{\text{products}}{\sum nS^{\circ}}-\underset{\text{reactants}}{\sum mS^{\circ}}[/latex]
where n and m are the coefficients found in the balanced chemical equation of the reaction.
Example 7.8
Determine the change in the standard entropy, ΔS°, for the synthesis of carbon dioxide from graphite and oxygen:
C(s) + O2(g) → CO2(g)
Solution
[latex]\begin{align*} \Delta S^{\circ}&=\underset{\text{products}}{\sum nS^{\circ}}-\underset{\text{reactants}}{\sum mS^{\circ}} \\ &=(213.8\text{ J/mol K})-(205.2\text{ J/mol K}+ 5.7\text{ J/mol K}) \\ &=+2.9\text{ J/mol K} \end{align*}[/latex]
Entropy Changes in the Surroundings
The second law of thermodynamics states that a spontaneous reaction will result in an increase of entropy in the universe. The universe comprises both the system being examined and its surroundings.
[latex]\Delta S_{\text{universe}}=\Delta S_{\text{sys}}+\Delta S_{\text{surr}}[/latex]
Standard entropy change can also be calculated by the following:
[latex]\Delta S^{\circ}{}_{\text{universe}}=\Delta S^{\circ}{}_{\text{sys}}+\Delta S^{\circ}{}_{\text{surr}}[/latex]
The change in entropy of the surroundings is essentially just a measure of how much energy is being taken in or given off by the system. Under isothermal conditions, we can express the entropy change of the surroundings as:
[latex]\Delta\text{S}_\text{surr}=\dfrac{{-q}_{\text{sys}}}{T}\text{ or }\Delta\text{S}_\text{surr}=\dfrac{-\Delta H_{\text{sys}}}{T}\hspace{1em}\text{(at constant pressure)}[/latex]
Example 7.9
For the previous example, the change in the standard entropy, ΔS°, for the synthesis of carbon dioxide from graphite and oxygen, use the previously calculated ΔS°sys and standard enthalpy of formation values to determine S°surr and ΔS°universe.
Solution
First we should solve for the ΔH°sys using the standard enthalpies of formation values:
[latex]\begin{align*} \Delta H^{\circ}{}_{\text{sys}}&=\Delta H^{\circ}{}_{\text{f}}[\ce{CO2(g)}]-\Delta H^{\circ}{}_{\text{f}}[\ce{C(s)}+\ce{O2(g)}] \\ &=(-393.5\text{ kJ/mol})-(0\text{ kJ/mol}+0\text{ kJ/mol}) \\ &=-393.5\text{ kJ/mol} \end{align*}[/latex]
Now we can convert this to the ΔS°surr:
[latex]\Delta S^{\circ}{}_{\text{surr}}=\dfrac{-\Delta H_{\text{sys}}}{T}=\dfrac{-393.5\text{ kJ/mol}}{298\text{ K}}=-1.32\text{ kJ/mol K}[/latex]
Finally, solve for ΔS°universe:
[latex]\begin{align*} \Delta S^{\circ}{}_{\text{universe}}&=\Delta S^{\circ}{}_{\text{sys}}+\Delta S^{\circ}{}_{\text{surr}} \\ &=(+2.9\text{ J/mol K})+(-1.32\times 10^3\text{ J/mol K}) \\ &=-1.3\times 10^3\text{ J/mol K} \end{align*}[/latex]
Key Takeaways
- Entropy is the level of randomness (or disorder) of a system. It could also be thought of as a measure of the energy dispersal of the molecules in the system.
- Microstates are the number of different possible arrangements of molecular position and kinetic energy at a particular thermodynamic state.
- Any change that results in a higher temperature, more molecules, or a larger volume yields an increase in entropy.
- At absolute zero (0 K), the entropy of a pure, perfect crystal is zero.
- The entropy of a substance can be obtained by measuring the heat required to raise the temperature a given amount, using a reversible process.
- The standard molar entropy, S°, is the entropy of 1 mole of a substance in its standard state, at 1 atm of pressure.
Media Attributions
- “Portrait of Ludwig Boltzmann” © American Institute of Physics, Emilio Segrè Visual Archives, Segrè Collection is licensed under a Public Domain license
- These tables are based on a table from UC Davis ChemWiki by University of California\CC-BY-SA-3.0 ↵

