9.6 Colligative Properties

Learning Objectives

  1. Determine the colligative properties of solutions of ionic solutes.

Do solutions with ionic solutes exhibit colligative properties?

There is a complicating factor: ionic solutes separate into ions when they dissolve. This increases the total number of particles dissolved in solution and increases the impact on the resulting colligative property. Historically, this greater-than-expected impact on colligative properties was one main piece of evidence for ionic compounds separating into ions (increased electrical conductivity was another piece of evidence).

For example, when NaCl dissolves, it separates into two ions:

NaCl(s) → Na+(aq) + Cl−(aq)

This means that a 1 M solution of NaCl actually has a net particle concentration of 2 M. The observed colligative property will then be twice as large as expected for a 1 M solution.

It is easy to incorporate this concept into our equations to calculate the respective colligative property. We define the van’t Hoff factor (i) as the number of particles each solute formula unit breaks apart into when it dissolves. Previously, we have always tacitly assumed that the van’t Hoff factor is simply 1. But for some ionic compounds, i is not 1, as shown in Table 9.3 “Ideal van’t Hoff Factors for Ionic Compounds”.

Table 9.3 Ideal van’t Hoff Factors for Ionic Compounds
Compound i
NaCl 2
KBr 2
LiNO3 2
CaCl2 3
Mg(C2H3O2)2 3
FeCl3 4
Al2(SO4)3 5

The ideal van’t Hoff factor is equal to the number of ions that form when an ionic compound dissolves.

Example 9.15

Predict the van’t Hoff factor for Sr(OH)2.

Solution
When Sr(OH)2 dissolves, it separates into one Sr2+ ion and two OH− ions:

Sr(OH)2 → Sr2+(aq) + 2OH−(aq)

Because it breaks up into three ions, its van’t Hoff factor is 3.

Test Yourself
What is the van’t Hoff factor for Fe(NO3)3?

Answer
4

All pure liquids have a characteristic vapor pressure in equilibrium with the liquid phase, the partial pressure of which is dependent on temperature. Solutions, however, have a lower vapor pressure than the pure solvent has, and the amount of lowering is dependent on the fraction of solute particles, as long as the solute itself does not have a significant vapor pressure (the term nonvolatile is used to describe such solutes). This colligative property is called vapor pressure depression (or lowering). Vapor pressure depression is rationalized by presuming that solute particles take positions at the surface in place of solvent particles, so not as many solvent particles can evaporate.

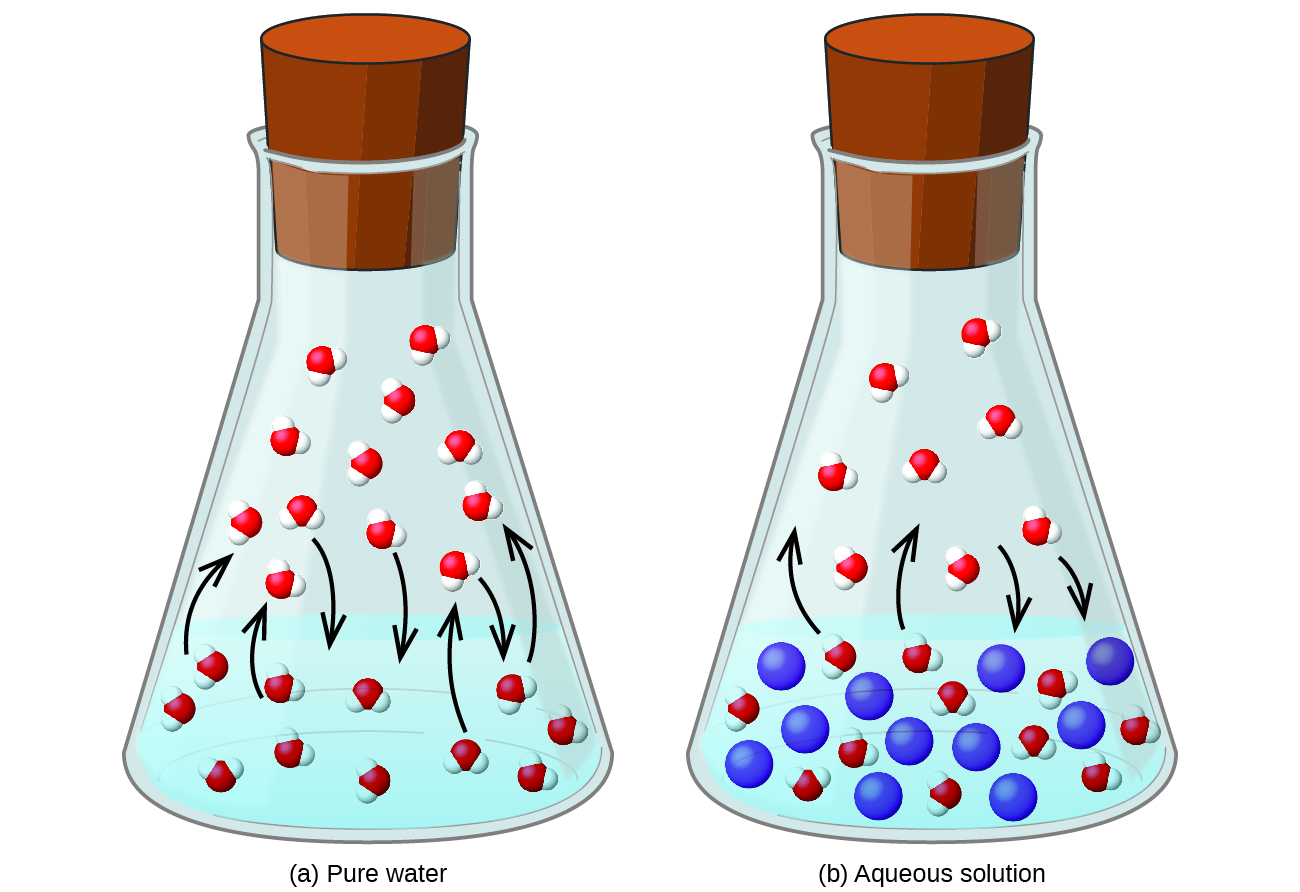
This figure contains two images. Figure a is labeled “pure water.” It shows a beaker half-filled with liquid. In the liquid, eleven molecules are evenly dispersed in the liquid each consisting of one central red sphere and two slightly smaller white spheres are shown. Four molecules near the surface of the liquid have curved arrows drawn from them pointing to the space above the liquid in the beaker. Above the liquid, twelve molecules are shown, with arrows pointing from three of them into the liquid below. Figure b is labeled “Aqueous solution.” It is similar to figure a except that eleven blue spheres, slightly larger in size than the molecules, are dispersed evenly in the liquid. Only four curved arrows appear in this diagram with two from the molecules in the liquid pointing to the space above and two from molecules in the space above the liquid pointing into the liquid below.

Image is taken from OpenStax: licensed under a Creative Commons Attribution 4.0 International License

Because the vapor pressure of a solution with a nonvolatile solute is depressed compared to that of the pure solvent, it requires a higher temperature for the solution’s vapor pressure to reach 1.00 atm (760 torr). Recall that this is the definition of the normal boiling point: the temperature at which the vapor pressure of the liquid equals 1.00 atm. As such, the normal boiling point of the solution is higher than that of the pure solvent. This property is called boiling point elevation.

Food and Drink App: Salting Pasta Cooking Water

When cooking dried pasta, many recipes call for salting the water before cooking the pasta. Some argue — with colligative properties on their side — that adding salt to the water raises the boiling point, thus cooking the pasta faster. Is there any truth to this?

To judge the veracity of this claim, we can calculate how much salt should be added to the water to raise the boiling temperature by 1.0°C, with the presumption that dried pasta cooks noticeably faster at 101°C than at 100°C (although a 1° difference may make only a negligible change in cooking times). We can calculate the molality that the water should have:

[latex]\begin{array}{rrl} 1.0^{\circ}\text{C}&=&m\left(0.512^{\circ}\text{C}/m\right) \\ \\ m&=&1.95 \end{array}[/latex]

We have ignored the van’t Hoff factor in our estimation because this obviously is not a dilute solution. Let us further assume that we are using 4 L of water (which is very close to 4 qt, which in turn equals 1 gal). Because 4 L of water is about 4 kg (it is actually slightly less at 100°C), we can determine how much salt (NaCl) to add:

[latex]4\cancel{\text{ kg }\ce{H2O}}\times \dfrac{1.95\text{mol NaCl}}{1\cancel{\text{ kg }\ce{H2O}}}\times \dfrac{58.5\text{ g NaCl}}{1\cancel{\text{ mol NaCl }}}=456.3\text{ g NaCl}[/latex]

This is just over 1 lb of salt and is equivalent to nearly 1 cup in the kitchen. In your experience, do you add almost a cup of salt to a pot of water to make pasta? Certainly not! A few pinches, perhaps one-fourth of a teaspoon, but not almost a cup! It is obvious that the little amount of salt that most people add to their pasta water is not going to significantly raise the boiling point of the water.

So why do people add some salt to boiling water? There are several possible reasons, the most obvious of which is taste: adding salt adds a little bit of salt flavour to the pasta. It cannot be much because most of the salt remains in the water, not in the cooked pasta. However, it may be enough to detect with our taste buds. The other obvious reason is habit; recipes tell us to add salt, so we do, even if there is little scientific or culinary reason to do so.

The boiling point of a solution is higher than the boiling point of the pure solvent, but the opposite occurs with the freezing point. The freezing point of a solution is lower than the freezing point of the pure solvent. Think of this by assuming that solute particles interfere with solvent particles coming together to make a solid, so it takes a lower temperature to get the solvent particles to solidify. This is called freezing point depression.

Freezing point depression is one colligative property we use in everyday life. Many antifreezes used in automobile radiators use solutions that have a lower freezing point than normal so that automobile engines can operate at subfreezing temperatures. We also take advantage of freezing point depression when we sprinkle various compounds on ice to thaw it in the winter for safety (see Figure 9.5 “Salt and Safety”). The compounds make solutions that have a lower freezing point, so rather than forming slippery ice, any ice is liquefied and runs off, leaving a safer pavement behind.

Salt or other compounds take advantage of the freezing point depression to minimize the formation of ice on sidewalks and roads, thus increasing safety. Source: “Salt, road, and cover” by Phil Romans is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 2.0 Generic.
Figure 9.5 “Salt and Safety.” Salt or other compounds take advantage of the freezing point depression to minimize the formation of ice on sidewalks and roads, thus increasing safety.

Before we introduce the final colligative property, we need to present a new concept. A semipermeable membrane is a thin membrane that will pass certain small molecules but not others. A thin sheet of cellophane, for example, acts as a semipermeable membrane.

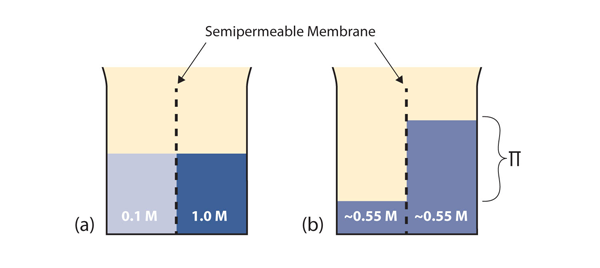
Consider the system in part (a) of Figure 11.3 “Osmosis.” A semipermeable membrane separates two solutions having the different concentrations marked. Curiously, this situation is not stable; there is a tendency for water molecules to move from the dilute side (on the left) to the concentrated side (on the right) until the concentrations are equalized, as in part (b) of Figure 9.6. This tendency is called osmosis. In osmosis, the solute remains in its original side of the system; only solvent molecules move through the semipermeable membrane. In the end, the two sides of the system will have different volumes. Because a column of liquid exerts a pressure, there is a pressure difference Π on the two sides of the system that is proportional to the height of the taller column. This pressure difference is called the osmotic pressure, which is a colligative property.

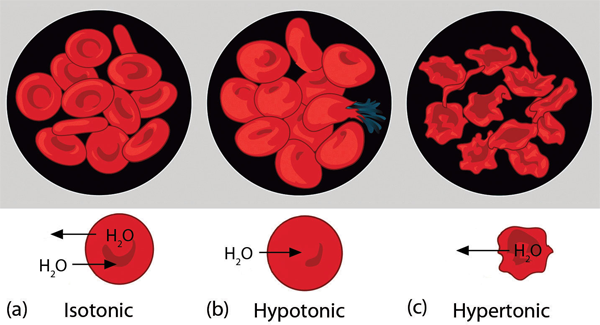
Figure 9.6 Osmosis. (a) Two solutions of differing concentrations are placed on either side of a semipermeable membrane. (b) When osmosis occurs, solvent molecules selectively pass through the membrane from the dilute solution to the concentrated solution, diluting it until the two concentrations are the same. The pressure exerted by the different height of the solution on the right is called the osmotic pressure.

Osmotic pressure is important in biological systems because cell walls are semipermeable membranes. In particular, when a person is receiving intravenous (IV) fluids, the osmotic pressure of the fluid needs to be approximately the same as blood serum; otherwise bad things can happen. Figure 9.7 “Osmotic Pressure and Red Blood Cells” shows three red blood cells: (a) a healthy red blood cell; (b) a red blood cell that has been exposed to a lower concentration than normal blood serum (a so-called hypotonic solution) so that the cell has plumped up as solvent moves into the cell to dilute the solutes inside; and (c) a red blood cell exposed to a higher concentration than normal blood serum (hypertonic) such that water leaves the red blood cell and it collapses onto itself. Only when the solutions inside and outside the cell are the same (isotonic) will the red blood cell be able to do its job.

Figure 9.7 “Osmotic Pressure and Red Blood Cells.” (a) This is what a normal red blood cell looks like. (b) When a red blood cell is exposed to a hypotonic solution, solvent goes through the cell membrane and dilutes the inside of the cell. (c) When a red blood cell is exposed to a hypertonic solution, solvent goes from the cell to the surrounding solution, diluting the hypertonic solution and collapsing the cell. Neither of these last two cases is desirable, so IV solutions must be isotonic with blood serum to not cause deleterious effects.

Osmotic pressure is also the reason you should not drink seawater if you’re stranded in a lifeboat on an ocean; seawater has a higher osmotic pressure than most of the fluids in your body. You can drink the water, but ingesting it will pull water out of your cells as osmosis works to dilute the seawater. Ironically, your cells will die of thirst, and you will also die. (It is OK to drink the water if you are stranded on a body of freshwater, at least from an osmotic pressure perspective.) Osmotic pressure is also thought to be important — in addition to capillary action — in getting water to the tops of tall trees.

Key Takeaways

  • Colligative properties depend only on the number of dissolved particles (that is, theconcentration), not their identity.
  • For ionic solutes, the calculation of colligative properties must include the fact that thesolutes separate into multiple particles when they dissolve.
  •  The equations for calculating colligative properties of solutions of ionic solvents includethe van’t Hoff factor, i.
  •  The boiling points of solutions are always higher, and the freezing points of solutions arealways lower, than those of the pure solvent.
  •  Osmotic pressure is caused by concentration differences between solutions separatedby a semipermeable membrane and is an important biological issue.

Exercises

Questions

  1. Explain why we need to consider a van’t Hoff factor for ionic solutes but not for molecular solutes.
  2. NaCl is often used in winter to melt ice on roads and sidewalks, but calcium chloride (CaCl2) is also used. Which would be better (on a mole-by-mole basis), and why?
  3. What are the three colligative properties that involve phase changes?
  4. Which colligative property does not involve a phase change? Give an example of its importance.

Answers

  1. Ionic solutes separate into more than one particle when they dissolve, whereas molecular solutes do not.
  1. Boiling point elevation, freezing point depression, vapor pressure depression

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem&121: Introduction to Chemistry Copyright © 2023 by Lake Washington Institute of Technology is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book