Learning Objectives
- Learn what is meant by the term gas laws.
- Learn and apply Boyle’s law.
- Learn and apply Charles’s law.
- Review other simple gas laws.
- Learn and apply the combined gas law.
When seventeenth-century scientists began studying the physical properties of gases, they noticed simple relationships between some of the measurable properties of gases. Take pressure (P) and volume (V), for example. Scientists noted that for a given amount of a gas (usually expressed in units of moles [n]), if the temperature (T) of the gas is kept constant, pressure and volume are related: as one increases, the other decreases. As one decreases, the other increases. We say that pressure and volume are inversely related.
There is more to it, however: pressure and volume of a given amount of gas at a constant temperature are numerically related. If you take the pressure value and multiply it by the volume value, the product is a constant for a given amount of gas at a constant temperature:
P × V = constant at constant n and T
If either volume or pressure changes while the amount and temperature stay the same, then the other property must change so that the product of the two properties still equals that same constant. That is, if the original conditions are labelled P1 and V1 and the new conditions are labelled P2 and V2, we have:
P1V1 = constant = P2V2
where the properties are assumed to be multiplied together. Leaving out the middle part, we have simply:
P1V1 = P2V2 at constant n and T
This equation is an example of a gas law. A gas law is a simple mathematical formula that allows you to model, or predict, the behaviour of a gas. This particular gas law is called Boyle’s law, after the English scientist Robert Boyle, who first announced it in 1662. Figure 8.35 Boyle’s Law shows two representations of what Boyle’s law describes.
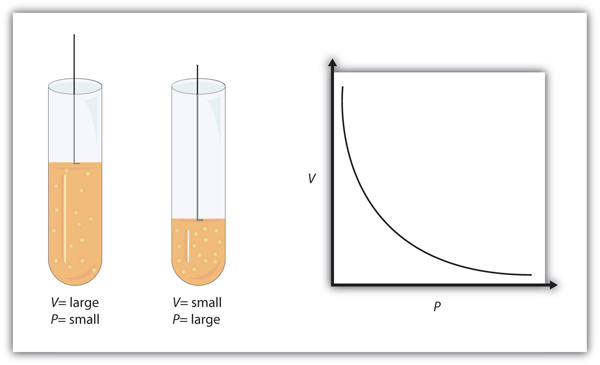
A piston having a certain pressure and volume (left piston) will have half the volume when its pressure is twice as much (right piston). One can also plot P versus V for a given amount of gas at a certain temperature; such a plot will look like the graph on the right.
Boyle’s law is an example of a second type of mathematical problem we see in chemistry—one based on a mathematical formula. Tactics for working with mathematical formulas are different from tactics for working with conversion factors. First, most of the questions you will have to answer using formulas are word-type questions, so the first step is to identify what quantities are known and assign them to variables. Second, in most formulas, some mathematical rearrangements (i.e., algebra) must be performed to solve for an unknown variable. The rule is that to find the value of the unknown variable, you must mathematically isolate the unknown variable by itself and in the numerator of one side of the equation. Finally, units must be consistent. For example, in Boyle’s law there are two pressure variables, and they must have the same unit. There are also two volume variables; they also must have the same unit. In most cases, it won’t matter what the unit is, but the unit must be the same on both sides of the equation.
Example 8.6
Problem
A sample of gas has an initial pressure of 2.44 atm and an initial volume of 4.01 L. Its pressure changes to 1.93 atm. What is the new volume if temperature and amount are kept constant?
Solution
First, determine what quantities we are given. We are given an initial pressure and an initial volume, so let these values be P1 and V1:
P1 = 2.44 atm and V1 = 4.01 L
We are given another quantity, final pressure of 1.93 atm, but not a final volume. This final volume is the variable we will solve for.
P2 = 1.93 atm and V2 = ? L
Substituting these values into Boyle’s law, we get:
[latex](2.44\text{ atm})(4.01\text{ L})=(1.93\text{ atm})V_2[/latex]
To solve for the unknown variable, we isolate it by dividing both sides of the equation by 1.93 atm — both the number and the unit:
[latex]\dfrac{(2.44\text{ atm})(4.01\text{ L})}{1.93\text{ atm}}=\dfrac{(1.93\text{ atm})V_2}{1.93\text{ atm}}[/latex]
Note that, on the left side of the equation, the unit atm is in the numerator and the denominator of the fraction. They cancel algebraically, just as a number would. On the right side, the unit atm and the number 1.93 are in the numerator and the denominator, so the entire quantity cancels:
[latex]\dfrac{(2.44\cancel{\text{ atm})}(4.01\text{ L})}{1.93\cancel{ \text{atm}}}=\dfrac{\cancel{(1.93\text{ atm})}V_2}{\cancel{1.93\text{ atm}}}[/latex]
What we have left is:
[latex]\dfrac{(2.44)(4.01\text{ L})}{1.93}=V_2[/latex]
Now we simply multiply and divide the numbers together and combine the answer with the L unit, which is a unit of volume. Doing so, we get:
V2 = 5.07 L
Does this answer make sense? We know that pressure and volume are inversely related; as one decreases, the other increases. Pressure is decreasing (from 2.44 atm to 1.93 atm), so volume should be increasing to compensate, and it is (from 4.01 L to 5.07 L). So the answer makes sense based on Boyle’s law.
Test Yourself
If P1 = 334 torr, V1 = 37.8 mL, and P2 = 102 torr, what is V2?
Answer
124 mL
As mentioned, you can use any units for pressure or volume, but both pressures must be expressed in the same units, and both volumes must be expressed in the same units.
Example 8.7
Problem
A sample of gas has an initial pressure of 722 torr and an initial volume of 88.8 mL. Its volume changes to 0.663 L. What is the new pressure?
Solution
We can still use Boyle’s law to answer this, but now the two volume quantities have different units. It does not matter which unit we change, as long as we perform the conversion correctly. Let us change the 0.663 L to milliliters:
[latex]0.663\cancel{\text{ L}}\times \dfrac{1000\text{ mL}}{1\cancel{\text{ L}}}=663\text{ mL}[/latex]
Now that both volume quantities have the same units, we can substitute into Boyle’s law:
[latex]\begin{array}{rrl} (722\text{ torr})(88.8\text{ mL})&=&P_2(663\text{ mL}) \\ \\ \dfrac{(722\text{ torr})(88.8\text{ mL})}{663\text{ mL}}&=&P_2 \end{array}[/latex]
The mL units cancel, and we multiply and divide the numbers to get:
P2 = 96.7 torr
The volume is increasing, and the pressure is decreasing, which is as expected for Boyle’s law.
Test Yourself
If V1 = 456 mL, P1 = 308 torr, and P2 = 1.55 atm, what is V2?
Answer
119 mL
There are other measurable characteristics of a gas. One of them is temperature (T). One could vary the temperature of a gas sample and note what effect it has on the other properties of the gas. Early scientists did just this, discovering that if the amount of a gas and its pressure are kept constant, then changing the temperature changes the volume (V). As temperature increases, volume increases; as temperature decreases, volume decreases. We say that these two characteristics are directly related.
A mathematical relationship between V and T should be possible except for one question: What temperature scale should we use? We know that science uses several possible temperature scales. Experiments show that the volume of a gas is related to its absolute temperature in Kelvin, not its temperature in degrees Celsius. If the temperature of a gas is expressed in kelvins, then experiments show that the ratio of volume to temperature is a constant:
[latex]\dfrac{V}{T}=\text{constant}[/latex]
We can modify this equation as we modified Boyle’s law: the initial conditions V1 and T1 have a certain value, and the value must be the same when the conditions of the gas are changed to some new conditions V2 and T2, as long as pressure and the amount of the gas remain constant. Thus, we have another gas law:
[latex]\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\text{ at constant }P\text{ and }n[/latex]
This gas law is commonly referred to as Charles’s law, after the French scientist Jacques Charles, who performed experiments on gases in the 1780s. The tactics for using this mathematical formula are similar to those for Boyle’s law. To determine an unknown quantity, use algebra to isolate the unknown variable by itself and in the numerator; the units of similar variables must be the same. But we add one more tactic: all temperatures must be expressed in the absolute temperature scale (Kelvin). As a reminder, we review the conversion between the absolute temperature scale and the Celsius temperature scale:
K = °C + 273
where K represents the temperature in kelvins, and °C represents the temperature in degrees Celsius.
Figure 8.36 “Charles’s Law” shows two representations of how Charles’s law works.
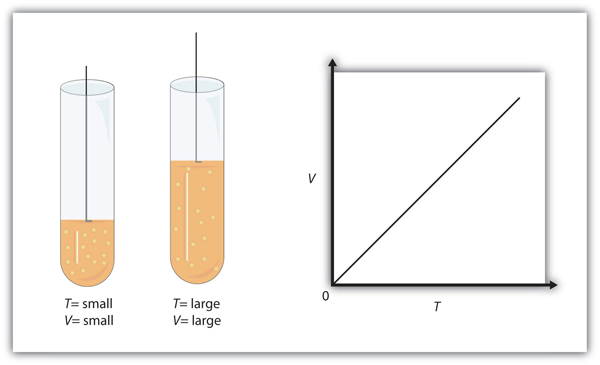
Example 8.8
Problem
A sample of gas has an initial volume of 34.8 mL and an initial temperature of 315 K. What is the new volume if the temperature is increased to 559 K? Assume constant pressure and amount for the gas.
Solution
First, we assign the given values to their variables. The initial volume is V1, so V1 = 34.8 mL, and the initial temperature is T1, so T1 = 315 K. The temperature is increased to 559 K, so the final temperature T2 = 559 K. We note that the temperatures are already given in kelvins, so we do not need to convert the temperatures. Substituting into the expression for Charles’s law yields:
[latex]\dfrac{34.8\text{ mL}}{315\text{ K}}=\dfrac{V_2}{559\text{ K}}[/latex]
We solve for V2 by algebraically isolating the V2 variable on one side of the equation. We do this by multiplying both sides of the equation by 559 K (number and unit). When we do this, the temperature unit cancels on the left side, while the entire 559 K cancels on the right side:
[latex]\dfrac{(559\text{ }\cancel{\text{K}})(34.8\text{ mL})}{315\text{ }\cancel{\text{K}}}=\dfrac{V_2\cancel{(559\text{ K})}}{\cancel{559\text{ K}}}[/latex]
The expression simplifies to:
[latex]\dfrac{(559)(34.8\text{ mL})}{315}=V_2[/latex]
By multiplying and dividing the numbers, we see that the only remaining unit is mL, so our final answer is:
V2 = 61.8 mL
Does this answer make sense? We know that as temperature increases, volume increases. Here, the temperature is increasing from 315 K to 559 K, so the volume should also increase, which it does.
Test Yourself
If V1 = 3.77 L and T1 = 255 K, what is V2 if T2 = 123 K?
Answer
1.82 L
It is more mathematically complicated if a final temperature must be calculated because the T variable is in the denominator of Charles’s law. There are several mathematical ways to work this, but perhaps the simplest way is to take the reciprocal of Charles’s law. That is, rather than write it as:
[latex]\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}[/latex]
write the equation as:
[latex]\dfrac{T_1}{V_1}=\dfrac{T_2}{V_2}[/latex]
It is still an equality and a correct form of Charles’s law, but now the temperature variable is in the numerator, and the algebra required to predict a final temperature is simpler.
Example 8.9
Problem
A sample of a gas has an initial volume of 34.8 L and an initial temperature of −67°C. What must be the temperature of the gas for its volume to be 25.0 L?
Solution
Here, we are looking for a final temperature, so we will use the reciprocal form of Charles’s law. However, the initial temperature is given in degrees Celsius, not kelvins. We must convert the initial temperature to kelvins:
−67°C + 273 = 206 K
In using the gas law, we must use T1 = 206 K as the temperature. Substituting into the reciprocal form of Charles’s law, we get:
[latex]\dfrac{206\text{ K}}{34.8\text{ L}}=\dfrac{T_2}{25.0\text{ L}}[/latex]
Bringing the 25.0 L quantity over to the other side of the equation, we get:
[latex]\dfrac{(25.0\text{ }\cancel{\text{L}})(206\text{ K})}{34.8\text{ }\cancel{\text{L}}}=T_2[/latex]
The L units cancel, so our final answer is:
T2 = 148 K
This is also equal to −125°C. As temperature decreases, volume decreases, which it does in this example.
Test Yourself
If V1 = 623 mL, T1 = 255°C, and V2 = 277 mL, what is T2?
Answer
235 K, or −38°C
Other Gas Laws
You may notice in Boyle’s law and Charles’s law that we actually refer to four physical properties of a gas: pressure (P), volume (V), temperature (T), and amount (in moles, n). We do this because these are the only four independent physical properties of a gas. There are other physical properties, but they are all related to one (or more) of these four properties.
Boyle’s law is written in terms of two of these properties, with the other two being held constant. Charles’s law is written in terms of two different properties, with the other two being held constant. It may not be surprising to learn that there are other gas laws that relate other pairs of properties—as long as the other two are held constant. Here we will mention a few.
Gay-Lussac’s law relates pressure with absolute temperature. In terms of two sets of data, Gay-Lussac’s law is:
[latex]\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}\text{ at constant }V\text{ and }n[/latex]
Note that it has a structure very similar to that of Charles’s law, only with different variables—pressure instead of volume. Avogadro’s law introduces the last variable for amount. The original statement of Avogadro’s law states that equal volumes of different gases at the same temperature and pressure contain the same number of particles of gas. Because the number of particles is related to the number of moles (1 mol = 6.022 × 1023 particles), Avogadro’s law essentially states that equal volumes of different gases at the same temperature and pressure contain the same amount (moles, particles) of gas. Put mathematically into a gas law, Avogadro’s law is:
[latex]\dfrac{V_1}{n_1}=\dfrac{V_2}{n_2}\text{ at constant }P\text{ and }T[/latex]
(First announced in 1811, it was Avogadro’s proposal that volume is related to the number of particles that eventually led to naming the number of things in a mole as Avogadro’s number.) Avogadro’s law is useful because for the first time we are seeing amount, in terms of the number of moles, as a variable in a gas law.
Example 8.10
Problem
A 2.45 L volume of gas contains 4.5 × 1021 gas particles. How many gas particles are there in 3.87 L if the gas is at constant pressure and temperature?
Solution
We can set up Avogadro’s law as follows:
[latex]\dfrac{2.45\text{ L}}{4.5\times 10^{21}\text{ particles}}=\dfrac{3.87\text{ L}}{n_2}[/latex]
We algebraically rearrange to solve for n2:
[latex]n_2=\dfrac{(3.87\text{ }\cancel{\text{L}})(4.5\times 10^{21}\text{ particles})}{2.45\text{ }\cancel{\text{L}}}[/latex]
The L units cancel, so we solve for n2:
n2 = 7.1 × 1021 particles
Test Yourself
A 12.8 L volume of gas contains 3.00 × 1020 gas particles. At constant temperature and pressure, what volume do 8.22 × 1018 gas particles fill?
Answer
0.351 L
The variable n in Avogadro’s law can also stand for the number of moles of gas in addition to the number of particles.
One thing we notice about all the gas laws is that, collectively, volume and pressure are always in the numerator, and temperature is always in the denominator. This suggests that we can propose a gas law that combines pressure, volume, and temperature. This gas law is known as the combined gas law, and its mathematical form is:
[latex]\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}\text{ at constant }n[/latex]
This allows us to follow changes in all three major properties of a gas. Again, the usual warnings apply about how to solve for an unknown algebraically (isolate it on one side of the equation in the numerator), units (they must be the same for the two similar variables of each type), and units of temperature (must be in kelvins).
Example 8.11
Problem
A sample of gas at an initial volume of 8.33 L, an initial pressure of 1.82 atm, and an initial temperature of 286 K simultaneously changes its temperature to 355 K and its volume to 5.72 L. What is the final pressure of the gas?
Solution
We can use the combined gas law directly; all the units are consistent with each other, and the temperatures are given in Kelvin. Substituting,
[latex]\dfrac{(1.82\text{atm})(8.33\text{ L})}{286\text{ K}}=\dfrac{P_2(5.72\text{ L})}{355\text{ K}}[/latex]
We rearrange this to isolate the P2 variable all by itself. When we do so, certain units cancel:
[latex]\dfrac{(1.82\text{ atm})(8.33\text{ }\cancel{\text{L}})(355\text{ }\cancel{\text{K}})}{(286\text{ }\cancel{\text{K}})(5.72\text{ }\cancel{\text{L}})}=P_2[/latex]
Multiplying and dividing all the numbers, we get:
P2 = 3.29 atm
Ultimately, the pressure increased, which would have been difficult to predict because two properties of the gas were changing.
Test Yourself
If P1 = 662 torr, V1 = 46.7 mL, T1 = 266 K, P2 = 409 torr, and T2 = 371 K, what is V2?
Answer
105 mL
As with other gas laws, if you need to determine the value of a variable in the denominator of the combined gas law, you can either cross-multiply all the terms or just take the reciprocal of the combined gas law. Remember, the variable you are solving for must be in the numerator and all by itself on one side of the equation.
Key Takeaways
- The behaviour of gases can be modelled with gas laws.
- Boyle’s law relates a gas’s pressure and volume at constant temperature and amount.
- Charles’s law relates a gas’s volume and temperature at constant pressure and amount.
- In gas laws, temperatures must always be expressed in kelvins.
- There are other gas laws that relate any two physical properties of a gas.
- The combined gas law relates pressure, volume, and temperature of a gas.
Exercises
Questions
- Define gas law. What restrictions are there on the units that can be used for the physical properties?
- What unit of temperature must be used for gas laws?
- Complete this sentence: Boyle’s law relates the [blank] of a gas inversely with the [blank] of that gas.
- Complete this sentence: Charles’s law relates the [blank] of a gas directly with the [blank] of that gas.
- What properties must be held constant when applying Boyle’s law?
- What properties must be held constant when applying Charles’s law?
- A gas has an initial pressure of 1.445 atm and an initial volume of 1.009 L. What is its new pressure if volume is changed to 0.556 L? Assume temperature and amount are held constant.
- A gas has an initial pressure of 633 torr and an initial volume of 87.3 mL. What is its new pressure if volume is changed to 45.0 mL? Assume temperature and amount are held constant.
- A gas has an initial pressure of 4.33 atm and an initial volume of 5.88 L. What is its new volume if pressure is changed to 0.506 atm? Assume temperature and amount are held constant.
- A gas has an initial pressure of 87.0 torr and an initial volume of 28.5 mL. What is its new volume if pressure is changed to 206 torr? Assume temperature and amount are held constant.
- A gas has an initial volume of 638 mL and an initial pressure of 779 torr. What is its final volume in litres if its pressure is changed to 0.335 atm? Assume temperature and amount are held constant.
- A gas has an initial volume of 0.966 L and an initial pressure of 3.07 atm. What is its final pressure in torr if its volume is changed to 3,450 mL? Assume temperature and amount are held constant.
- A gas has an initial volume of 67.5 mL and an initial temperature of 315 K. What is its new volume if temperature is changed to 244 K? Assume pressure and amount are held constant.
- A gas has an initial volume of 2.033 L and an initial temperature of 89.3 K. What is its volume if temperature is changed to 184 K? Assume pressure and amount are held constant.
- A gas has an initial volume of 655 mL and an initial temperature of 295 K. What is its new temperature if volume is changed to 577 mL? Assume pressure and amount are held constant.
- A gas has an initial volume of 14.98 L and an initial temperature of 238 K. What is its new temperature if volume is changed to 12.33 L? Assume pressure and amount are held constant.
- A gas has an initial volume of 685 mL and an initial temperature of 29°C. What is its new temperature if volume is changed to 1.006 L? Assume pressure and amount are held constant.
- A gas has an initial volume of 3.08 L and an initial temperature of −73°C. What is its new volume if its temperature is changed to 104°C? Assume pressure and amount are held constant.
- Use Gay-Lussac’s law to determine the final pressure of a gas whose initial pressure is 602 torr, initial temperature is 356 K, and final temperature is 277 K. Assume volume and amount are held constant.
- Use Gay-Lussac’s law to determine the final temperature of a gas whose initial pressure is 1.88 atm, initial temperature is 76.3 K, and final pressure is 6.29 atm. Assume volume and amount are held constant.
- If 3.45 × 1022 atoms of Ar have a volume of 1.55 L at a certain temperature and pressure, what volume do 6.00 × 1023 atoms of Ar have at the same temperature and pressure?
- If 5.55 × 1022 atoms of He occupy a volume of 2.06 L at 0°C at 1.00 atm pressure, what volume do 2.08 × 1023 atoms of He occupy under the same conditions?
- Use Avogadro’s law to determine the final volume of a gas whose initial volume is 6.72 L, initial amount is 3.88 mol, and final amount is 6.10 mol. Assume pressure and temperature are held constant.
- Use Avogadro’s law to determine the final amount of a gas whose initial volume is 885 mL, initial amount is 0.552 mol, and final volume is 1,477 mL. Assume pressure and temperature are held constant.
- Use the combined gas law to complete this table. Assume that the amount remains constant in all cases.
V1 P1 T1 V2 P2 T2 56.9 mL 334 torr 266 K 722 torr 334 K 0.976 L 2.33 atm 443 K 1.223 L 355 K 3.66 L 889 torr 23°C 2.19 L 739 torr - Use the combined gas law to complete this table. Assume that the amount remains constant in all cases.
V1 P1 T1 V2 P2 T2 56.7 mL 1.07 atm −34°C 998 torr 375 K 3.49 L 338 torr 45°C 1,236 mL 392 K 2.09 mL 776 torr 45°C 0.461 mL 0.668 atm - A gas starts at the conditions 78.9 mL, 3.008 atm, and 56°C. Its conditions change to 35.6 mL and 2.55 atm. What is its final temperature?
- The initial conditions of a sample of gas are 319 K, 3.087 L, and 591 torr. What is its final pressure if volume is changed to 2.222 L and temperature is changed to 299 K?
- A gas starts with initial pressure of 7.11 atm, initial temperature of 66°C, and initial volume of 90.7 mL. If its conditions change to 33°C and 14.33 atm, what is its final volume?
- A sample of gas doubles its pressure and doubles its absolute temperature. By what amount does the volume change?
Answers
- A gas law is a simple mathematical formula that allows one to predict the physical properties of a gas. The units of changing properties (volume, pressure, etc.) must be the same.
- pressure; volume
- amount of gas and temperature
- 2.62 atm
- 50.3 L
- 1.95 L
- 52.3 mL
- 260 K
- 444 K, or 171°C
19. 468 torr
21. 27.0 L
23. 10.6 L
25.
| V1 | P1 | T1 | V2 | P2 | T2 |
|---|---|---|---|---|---|
| 56.9 mL | 334 torr | 266 K | 33.1 mL | 722 torr | 334 K |
| 0.976 L | 2.33 atm | 443 K | 1.223 L | 1.49 atm | 355 K |
| 3.66 L | 889 torr | 23°C | 2.19 L | 739 torr | 147 K, or −126°C |
27. 126 K, or −147°C
29. 40.6 mL
Media Attributions
- “Boyle’s Law” by David W. Ball © CC BY-NC-SA (Attribution NonCommercial ShareAlike)

