Learning Objectives
- To examine the differences between ideal and real gases.
- To explore the effects of high pressure and low temperature on real gas samples.
- To apply van der Waals equation to correct the ideal gas law for real gases using the experimentally determined constants a and b.
An ideal gas is one that conforms exactly to the tenets of the kinetic molecular theory, where the volume occupied by the gas particles is negligible relative to the total volume of the container, and there are no appreciable intermolecular attractions or repulsions.
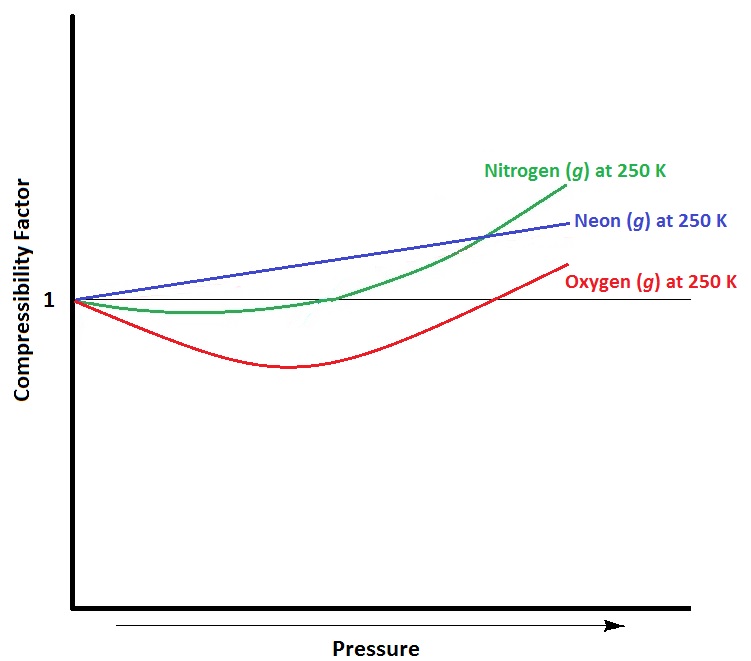
Real gases] can deviate from ideal behavior, especially at high pressures and low temperatures. The extent of deviation is measured using the compressibility factor. The compressibility factor is obtained by solving for n in the ideal gas law: dividing the product of pressure and volume by the product of the gas constant and temperature [latex]\left(\dfrac{PV}{RT}\right)[/latex] for one mole of a given substance. Under ideal conditions, this ratio of [latex]\left(\dfrac{PV}{RT}\right)[/latex] should be exactly equal to 1.
Real Gases at High Pressure
At higher pressures, gas molecules are closer together in a space. As a result of this crowding, gas molecules experience greater attractive intermolecular forces. Intermolecular forces hold molecules together more, lessening the force and frequency of collisions with the container wall and thus lowering the pressure below ideal values. As well, at higher pressure, molecules occupy a larger proportion of the volume of the container. With other gas molecules taking up a larger proportion of the volume of the container, the unoccupied volume of the container available to any one molecule is smaller than in ideal conditions. This decrease in available volume causes an increase in pressure beyond ideal conditions.
Real Gases at Low Temperature
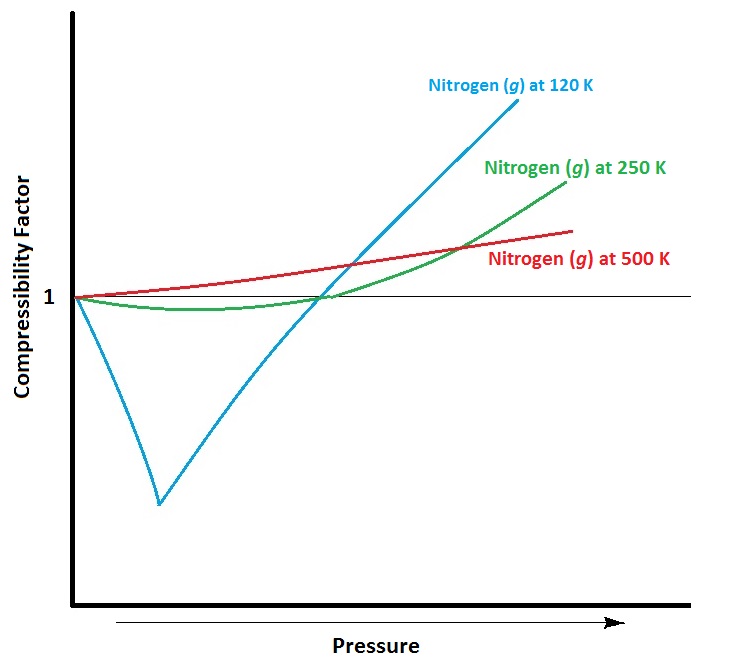
Temperature also influences deviations from ideal gas behavior. As temperature decreases, the average kinetic energy of the gas particles decreases. A larger proportion of gas molecules therefore have insufficient kinetic energy to overcome attractive intermolecular forces from neighboring atoms. This means that gas molecules become “stickier” to each other, and collide with the walls of the container with less frequency and force, decreasing pressure below that of ideal values.
The van der Waals Equation

In 1873, Dutch scientist Johannes van der Waals developed an equation that compensates for deviations from ideal gas behaviour. The van der Waals equationuses two additional experimentally determined constants: a, which is a term to correct for intermolecular forces, and b, which corrects for the volume of the gas molecules (see Table 8.5 “Selected van der Waals Constants for Gas Molecules”). The van der Waals equation appears as:
[latex]\left(P+\dfrac{an^2}{V^2}\right)(V-nb)=nRT[/latex]
It should be noted that, if the new terms a and b are equal to zero (under ideal conditions), the equation simplifies back to the ideal gas law: PV = nRT.
| Element | [latex]a \left(\dfrac{L^2\text{ atm}}{\text{mol}^2}\right)[/latex] | [latex]b \left(\dfrac{\text{L}}{\text{mol}}\right)[/latex] |
|---|---|---|
| Helium | 0.03457 | 0.0237 |
| Neon | 0.2135 | 0.01709 |
| Hydrogen | 0.2476 | 0.02661 |
| Argon | 1.355 | 0.0320 |
| Nitric oxide | 1.358 | 0.02789 |
| Oxygen | 1.378 | 0.03183 |
| Nitrogen | 1.408 | 0.03913 |
| Carbon monoxide | 1.505 | 0.03985 |
| Methane | 2.283 | 0.04278 |
| Krypton | 2.349 | 0.03978 |
| Carbon dioxide | 3.640 | 0.04267 |
| Hydrogen chloride | 3.716 | 0.04081 |
| Nitrous oxide | 3.832 | 0.04415 |
| Ammonia | 4.225 | 0.0371 |
| Xenon | 4.250 | 0.05105 |
Example 8.8
Problem
Use the van der Waals equation and Table 8.6 to determine the pressure, in atmospheres, of 2.00 moles of oxygen gas in a 30.00 L flask at 25.0°C.
Solution
[latex]\begin{array}{rrl} \left(P+a\left[\dfrac{n}{V}\right]^2\right)(V-nb)&=&nRT \\ \\ \left(P+1.378\dfrac{\text{L}^2\text{ atm}}{\text{mol}^2}\left[\dfrac{2.00\text{ mol}}{30.00\text{ L}}\right]\right)\left(30.00\text{ L}-2.00\text{ mol}\left(0.03183\dfrac{\text{L}}{\text{mol}}\right)\right)&=&2.00\text{ mol} \\ \\ (0.08206\text{ L atm K}^{-1}\text{ mol}^{-1})(298.15\text{ K})&=&P \\ \\ P&=&1.63\text{ atm} \end{array}[/latex]
Key Takeaways
- An ideal gas is one that conforms exactly to the tenets of the kinetic molecular theory, where the volume occupied by the gas particles is negligible relative to the total volume of the container and there are no appreciable intermolecular attractions or repulsions.
- A real gas is one that deviates from ideal behaviour, due to the effects of gas particles occupying a finite volume and the strength of intermolecular forces.
- The van der Waals equation compensates for deviations from ideal gas behaviour.
Media Attributions
- “Compressibility Factors” by Jessie A. Key © CC BY (Attribution)
- “Compressibility Factor of Nitrogen” by Jessie A. Key © CC BY (Attribution)
- “Johannes Diderik van der Waals” © Public Domain
- Adapted from Van der Waals constants (data page) on Wikipedia (under a CC BY-SA 3.0 licence). ↵

