5.14 IV Infusion by Gravity

[latexpage]

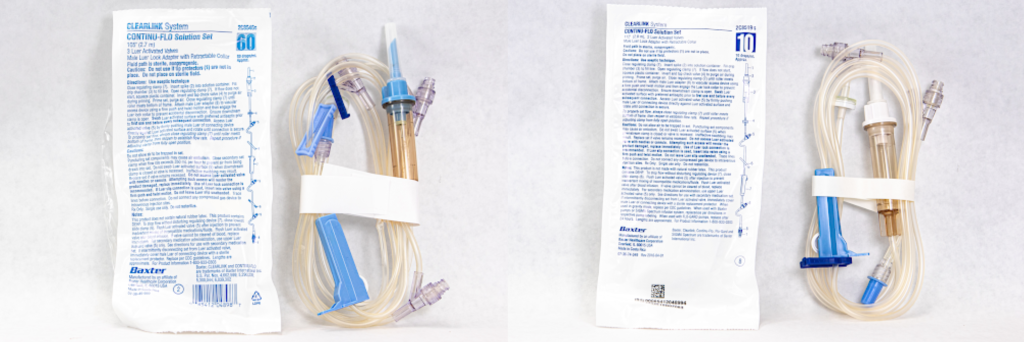
IV drip tubing comes in a variety of sizes called drop factors. The drop factor is the number of drops in one mL of solution using gravity IV tubing. The drop factor is printed on the IV tubing package. Macrodrip tubing includes tubing with drop factors of 10, 12, 15, or 20 drops per mililiter and is typically used to deliver general IV solutions to adults. Microdrip tubing includes tubing with a drop factor of 60 drops per milliliter. It is typically used to deliver precise amounts of medication in small drops to children and infants. See Figure 5.13^[1] for an image of microdrip and macrodrip tubing.

In the sample problems below, you will be calculating the number of drops needed per minute to achieve the quantity of fluid to be infused per hour in the provider order.

Practice Problem: IV Infusion (Example 1)

Let’s practice calculating the rate of IV infusion by gravity using macrodrip tubing.

Patient Information:

Name: Elaina Dimas, DOB: 12/09/20xx, Age 6, Allergies: NKDA, Weight: 15 kg

Diagnosis: Dehydration

Prescription: 0.9% Sodium Chloride 500 mL IV bolus over four hours

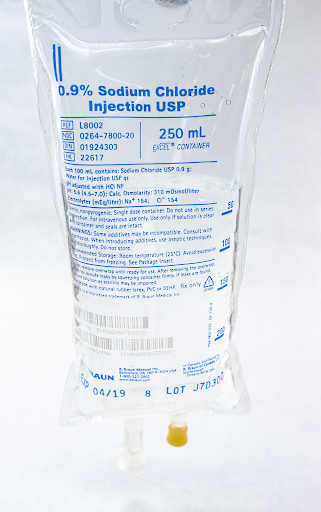
See Figure 5.14^[3] for the IV fluid supplied.

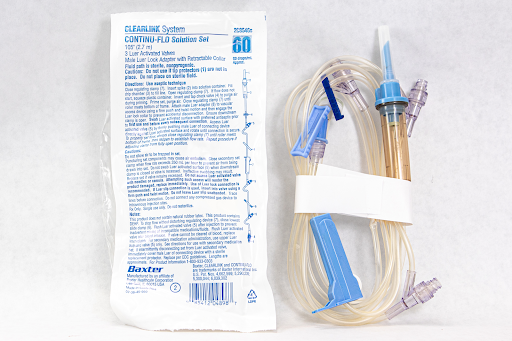
See Figure 5.15^[4] for IV tubing supplied.

Solve using dimensional analysis.

1. To set up the problem, begin by identifying the goal unit(s) for which we are solving. When calculating infusion rates by gravity, we need to calculate how many drops (gtts) of the solution will be infused each minute. This will allow us to count the actual drops dripping from the tubing and regulate the rate, so the volume of infusion is delivered in the time ordered. Set up the problem by identifying the goal unit to solve, but instead of solving for one unit, we will be solving for two units: drops (gtts) and minutes:

\[ \frac{gtts}{min}~=~?

\]

2. Set up the first fraction by matching drops (gtts) in the numerator to the goal unit. Review the tubing provided to determine how many drops per minute are administered with this type of tubing. In this example, the tubing is labelled as 60 gtts/mL. Place 60 in the numerator for how many drops are administered by the tubing in 1 mL, and then add 1 mL to the denominator:

\[\frac{gtts}{min}~=~\frac{60~gtts}{1~mL}

\]

3. Set up the second fraction with the intent to cross off mL, so place mL in the numerator. Look for information provided in the problem related to mL. The prescription is for 500 mL of solution over four hours. Place 500 into the numerator, and place 4 hours in the denominator, and then cross off the mL units:

\[

\frac{gtts}{min}~=~\frac{60~gtts}{1~\cancel{mL}}~x~\frac{500~\cancel{mL}}{4~hours}

\]

4. Calculate the minutes to achieve our goal unit of drops per minute. Create the third fraction with hour in the numerator with the intent to cross off hour units. Using equivalencies, we know that 1 hour is equivalent to 60 minutes, so plug in 60 minutes in the denominator. Cancel out hours. Evaluate if we have reached our goal units. This equation now matches the goal of units/min and can be solved:

\[

\frac{gtts}{min}~=~\frac{60~gtts}{1~\cancel{mL}}~x~\frac{500~\cancel{mL}}{4~\cancel{hours}}~x~\frac{1~\cancel{hour}}{60~min}

\]

5. Multiply across the numerators and denominators, and then divide the final fraction.

\[

\frac{gtts}{min}~=~\frac{60~gtts}{1~\cancel{mL}}~x~\frac{500~\cancel{mL}}{4~\cancel{hours}}~x~\frac{1~\cancel{hour}}{60~min}~=~\frac{60~gtts~x~500~x~1}{1~x~4~x~60~min}~=~{125~gtts/min}

\]

6. The final answer is 125 drops/minute.

Practice Problem: IV Infusion (Example 2)

Let’s practice a second problem using different types of IV drip tubing and a different time to be infused.

Patient Information:

Name: Amber Gomez, DOB: 08/26/20xx, Age 26, Allergies: NKDA, Weight: 50 kg

Provider Order: Lactated Ringers 250 mL IV bolus over 2 hours

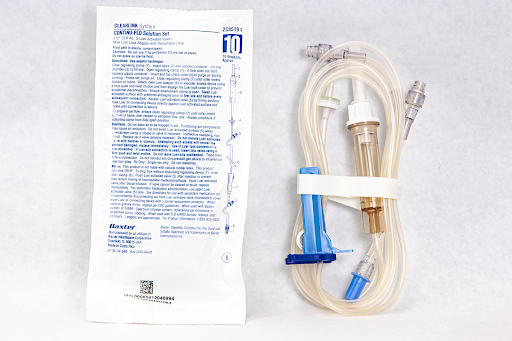
Fluid Supplied: See Figure 5.16^[5] for the fluid supplied.

Tubing Supplied: See Figure 5.17^[6] for the tubing available.

Solve using dimensional analysis:

\[\frac{gtts}{min}~=~\frac{10~gtts}{1~\cancel{mL}}~x~\frac{250~\cancel{mL}}{2~\cancel{hour}}~x~\frac{1~\cancel{hour}}{60~min}~=~\frac{10~gtts~x~250~x~1}{1~x~2~x~60~min}~=~{20.83~gtts/min}

\]

Round drops to the nearest whole number for a final answer of 21 drops/minute.

Practice flow rate calculations with the interactive activity below.